二次函数相关存在性问题.doc
《二次函数相关存在性问题.doc》由会员分享,可在线阅读,更多相关《二次函数相关存在性问题.doc(21页珍藏版)》请在冰豆网上搜索。
二次函数相关的存在性问题习题练习
一.等腰三角形存在性问题:
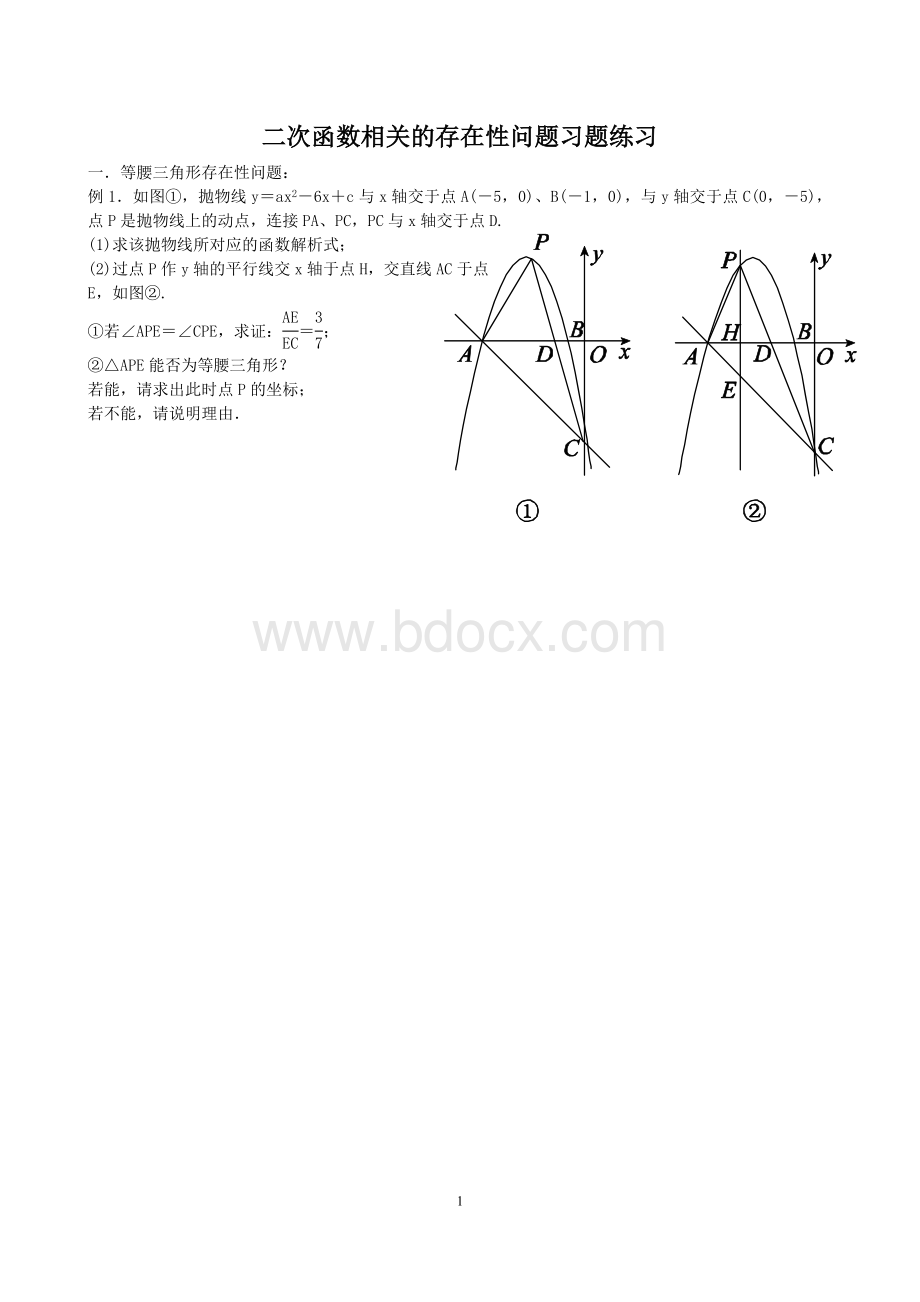
例1.如图①,抛物线y=ax2-6x+c与x轴交于点A(-5,0)、B(-1,0),与y轴交于点C(0,-5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.
(1)求该抛物线所对应的函数解析式;
(2)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图②.
①若∠APE=∠CPE,求证:
=;
②△APE能否为等腰三角形?
若能,请求出此时点P的坐标;
若不能,请说明理由.
针对训练:
1.如图①,抛物线y=ax2+bx+4交x轴于A、B两点(点A在点B左侧),交y轴于点C,连接AC、BC,其中CO=BO=2AO.
(1)求抛物线的解析式;
(2)点Q为直线BC上方的抛物线上一点,过点Q作QE∥AC交BC于E,作QN⊥x轴于N,交BC于M,当△EMQ的周长L最大时,求点Q的坐标及L的最大值;
(3)如图②,在
(2)的结论下,连接AQ分别交BC于F,交OC于G,四边形BOGF从F开始沿射线FC平移,同时点P从C开始沿折线CO-OB运动,且点P的运动速度为四边形BOGF平移速度的倍,当点P到达B点时,四边形BOGF停止运动.设四边形BOGF平移过程中对应的图形为B1O1G1F1,当△PFF1为等腰三角形时,求B1F的长度.
2.如图,在平面直角坐标系中,抛物线y=-x2+x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.现将抛物线以每秒个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转α°(0°<α<180°),记旋转中的△A′C′B为△A′′C′′B′,若直线A′′C′′与y轴交于点K,直线A′′C′′与直线AD交于点I,则△DKI是否能为等腰三角形?
若能,求出所有符合条件的KI的长;若不能,说明理由.
三角形全等、相似存在性问题:
例2.如图,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,且OA=1,OC=2,以O为直角顶点作Rt△COD,OD=3.已知二次函数y=x2+x-的图象过D、B两点,连接BD,E为射线DB上的一点,过E作EH⊥x轴于H,点P为抛物线对称轴上一点,且在x轴上方,点Q在第二象限的抛物线上,是否存在P、Q使得以P、O、Q为顶点的三角形与△DEH全等?
若存在,请求出点Q的坐标,如果不存在,请说明理由.
针对训练:
1.如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?
为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?
若存在,请指出直接写出点P的坐标;若不存在,请说明理由.
2.如图,已知一条直线过点(0,4),且与抛物线y=x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标.
(2)在x轴上是否存在点C,使得△ABC是直角三角形?
若存在,求出点C的坐标,若不存在,请说明理由.
3.如图,已知抛物线y=x2+x-4与x轴交于A、B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:
y=-x-4与x轴交于D点,点P是抛物线y=x2+x-4上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.过点P作PH⊥y轴,垂足为H,连接AC,PC,试问当P点横坐标为何值时,使得以点P,C,H为顶点的三角形与△ACD相似?
4.如图,已知抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,顶点为D,点N在抛物线上,其横坐标为.连接CN,点P为直线CN上的动点,点Q在抛物线上,连接CQ、PQ得△CPQ,当△CPQ为等腰直角三角形时,求线段CP的长度.
与四边形有关的存在性问题:
例3.如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使以A、C、F、G四个点为顶点的四边形是平行四边形?
如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
1.如图,抛物线y=a(x+1)2+4(a≠0)与x轴交于A,C两点,与直线y=x-1交于A,B两点,直线AB与抛物线的对称轴交于点E.连接CE,将△CEB补成矩形,使△CEB上的两个顶点成为矩形一边的两个顶点,第三个顶点落在矩形这一边的对边上,求出矩形未知顶点的坐标.
2.如图,抛物线y=x2+2x-3交x轴于点A,B.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
3.如图,在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:
y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);
(2)点E是直线l上方的抛物线上的一点,若△ACE面积的最大值为,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?
若能,求出点P的坐标;若不能,请说明理由.
二次函数相关的存在性问题答案
等腰三角形存在性问题:
例1.解:
(1)∵抛物线y=ax2-6x+c过点B(-1,0)、C(0,-5).
∴
解得
∴该抛物线为y=-x2-6x-5.
(2)①证明:
∵PE∥y轴,∴PH⊥AO,
∴∠AHP=∠DHP=90°.
又∵PH=PH,∠APE=∠CPE,
∴△AHP≌△DHP,∴AH=DH.
设点P(x,-x2-6x-5),
∴AH=DH=x-(-5)=x+5,PH=-x2-6x-5.
由PE∥y轴,得=,
则=.
∵x+5≠0,∴x+1=,解得x1=-,x2=0(不符合).
∴OH=,AH=,∴==.
②能,分三种情况讨论.
Ⅰ、若PA=PE.由OA=OC=5,
得∠AEP=∠PAE=∠ACO=45°,
∴∠APE=90°.此时点P与点B重合.
∴此时点P的坐标为(-1,0).
Ⅱ、若AP=AE.由题意,可得∠APE=∠AEP=45°,
又∵PH⊥AO,∴AH=PH,即-x2-6x-5=x+5.
解得x1=-2,x2=-5(不符合).
则y=3,则点P的坐标为(-2,3).
Ⅲ、∵点A、C的坐标为(-5,0)、(0,-5).
∴直线AC的解析式为y=-x-5.∴点E的坐标为(x,-x-5).
若AE=PE,则PE=|-x2-6x-5-(-x-5)|=|-x2-5x|.
又AE=AH=(x+5),
则-x2-5x=(x+5)或x2+5x=(x+5),
(x+5)(+x)=0或(x+5)(-x)=0.
解得:
x1=-,x2=-5(不符合),x3=,x4=-5(不符合).
当x1=-时,y1=6-7,当x3=时,y3=-6-7.
∴此时点P的坐标为(-,6-7)或(,-6-7).
综上所述可得点P的坐标为(-2,3)、(-1,0)、(-,6-7)或(,-6-7).
针对训练:
1.解:
(1)当x=0时,y=4,则C(0,4),
∴OC=4.
又∵OC=OB=2OA,
∴OB=4,OA=2,
∴B(4,0),A(-2,0).
又∵B(4,0),A(-2,0)在抛物线y=ax2+bx+4上,
∴∴
∴抛物线的解析式为y=-x2+x+4.
(2)∵B(4,0),C(0,4),∴直线BC的解析式为y=-x+4.
∴∠MBN=∠NMB=∠QME=45°,延长QE交y轴于R.
又∵EQ∥AC,OC∥QM,∴∠EQM=∠CRQ=∠ACO,
∴tan∠EQM=tan∠ACO==.
如图,过E作EH⊥QM于H,设EH=m,
则QH=2m,EQ=m,MH=m,EM=m,
∴QM=3m,∴m=QM.
设Q(x,-x2+x+4),则M(x,-x+4),
∴L=QM=
=(-x2+2x)
=-(x-2)2+,
又∵0(3)∵Q(2,4),A(-2,0),
∴AQ的解析式为y=x+2,∴G(0,2),F(1,3),
∴BF=B1F1=3,△CFG为等腰三角形.
设FF1=t,则PC=2t.∴F1(1-t,t+3),
当P在线段CO上运动时,则0①若FP=FF1时,则1+(1-2t)2=2t2,
∴t1=t2=1,∴FF1=t=,∴B1F=B1F1-FF1=2;
②若PF=PF1时,则1+(1-2t)2=(1-t)2+(1-3t)2,
∴t1=0,t2=.又∵0∴FF1=t=,∴B1F=B1F1-FF1=;
∴B1F=B1F1-FF1=4-2.
综上所述:
B1F=,,2或4-2.
③若F1P=F1F时,则(1-t)2+(1-3t)2=2t2,∴t1=t2=.
∴FF1=t=,∴B1F=B1F1-FF1=;
当P在线段OB上运动时,则2∵∠F1FP>90