运筹学中科大答案解析.docx
《运筹学中科大答案解析.docx》由会员分享,可在线阅读,更多相关《运筹学中科大答案解析.docx(17页珍藏版)》请在冰豆网上搜索。
运筹学中科大答案解析
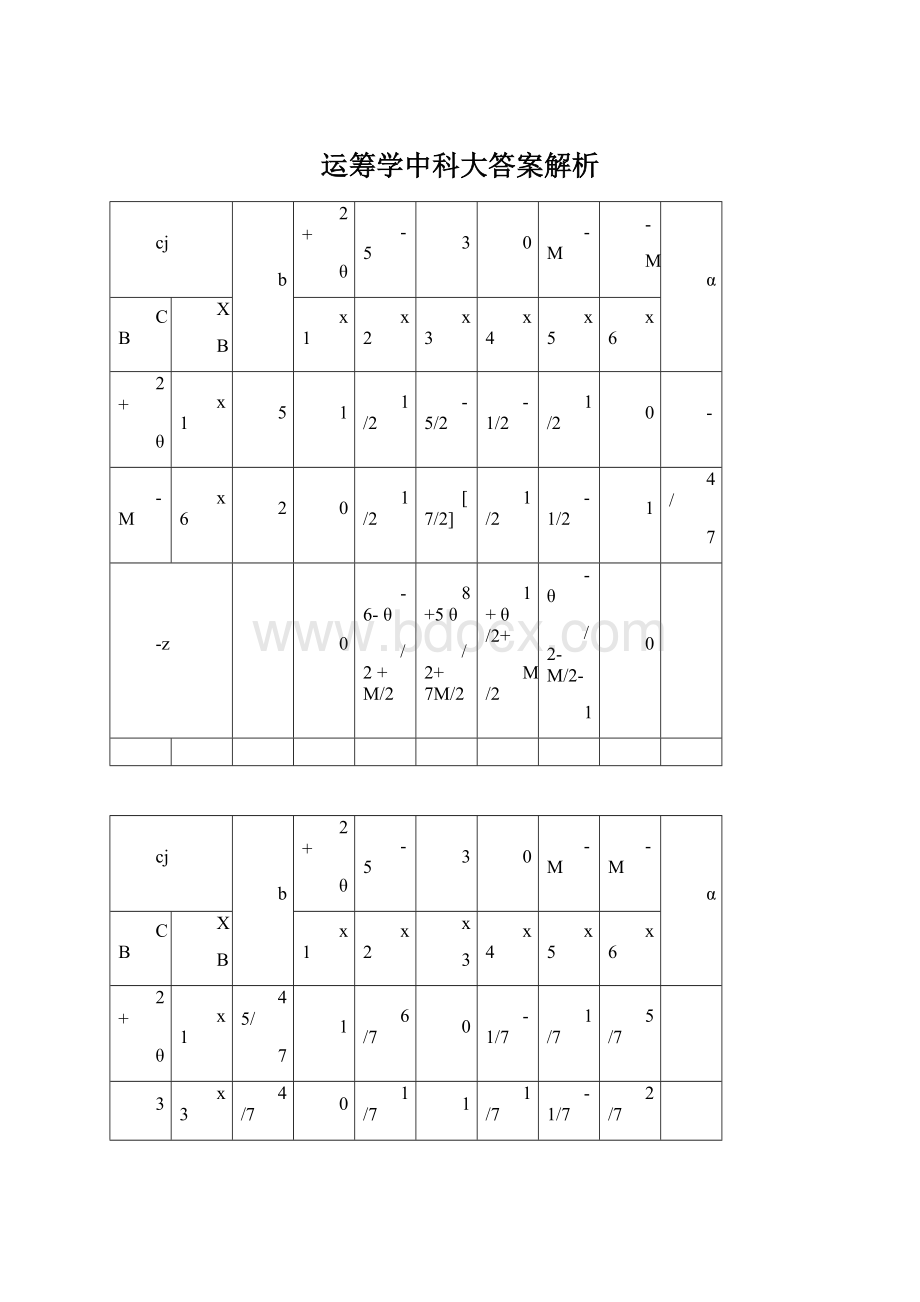
cj
b
2+
θ
-5
3
0
-M
-
M
α
CB
X
B
x1
x2
x3
x4
x5
x6
2+
θ
x1
5
1
1/2
-5/2
-1/2
1/2
0
-
-M
x6
2
0
1/2
[7/2]
1/2
-1/2
1
4/
7
-z
0
-6-θ
/2+M/2
8+5θ
/2+7M/2
1+θ/2+
M/2
-θ
/2-M/2-
1
0
cj
b
2+
θ
-5
3
0
-M
-M
α
CB
X
B
x1
x2
x
3
x4
x5
x6
2+
θ
x1
45/
7
1
6/7
0
-1/7
1/7
5/7
3
x3
4/7
0
1/7
1
1/7
-1/7
2/7
-z
0
-50/7-6
θ/7
0
-1/7+θ
/7
-M+1/7-
θ/7
-M-16/7-5
θ/7
时,最优解不变。
7
时,7
5061
7,即
777
5061
7,即
777
cj
b
2+
θ
-5
3
0
-M
-M
α
CB
X
B
x1
x2
x
3
x4
x5
x6
2+
θ
x1
45/
7
1
6/7
0
-1/7
1/7
5/7
15/
2
3
x3
4/7
0
[1/7]
1
1/7
-1/7
2/7
4
-z
0
-50/7-6
θ/7
0
-1/7+θ
/7
-M+1/7-
θ/7
-M-16/7-5
θ/7
cj
b
2+
θ
-
5
3
0
-M
-M
α
CB
X
B
x1
x
2
x3
x4
x5
x6
2+
θ
x1
3
1
0
-6
-1
1
-1
-5
x2
4
0
1
7
1
-1
2
-z
0
0
40+6
θ
7+
θ
-M-7
-θ
-M+12
+θ
14
(3)的最优解为(3,4,0)T,目标函数值为z3
模型
(1)的最优解为(3,29/7,0)T,目标函数值为z3145/7
(4)变化第一个约束条件时:
cj
b
2
-5
3
0
-M
-M
α
CB
Xb
x1
x2
x3
x4
x5
x6
-M
x5
10+s
[2]
1
-5
-1
1
0
5+s/2
-M
x6
7
1
1
1
0
0
1
7
-z
2+3M
-5+2M
3-4M
M
0
0
5s/27,即s4时
cj
b
2
-5
3
0
-M
-M
α
CB
XB
x1
x2
x3
x4
x5
x6
2
x1
5+s/2
1
1/2
-5/2
-1/2
1/2
0
-
-M
x6
2-s/2
0
1/2
[7/2]
1/2
-1/2
1
4/7-s/
7
-z
0
-6+M/
2
8+7M/
2
1+
M/2
-M/2-
1
0
cj
b
2
-5
3
0
-M
-M
α
CB
Xb
x1
x2
x3
x4
x5
x6
2
x1
45/7+s/
1
6/7
0
-1/7
1/7
5/7
7
3
x3
4/7-s/7
0
1/7
1
1/7
-1/7
2/7
-z
0
-50/7
0
-1/7
-M+1/
7
-M-16/
7
45s4s102s
此时最优解为(45s,0,4s)T,目标函数最大值为z102s
777
变化第二个约束条件时:
cj
b
2
-5
3
0
-M
-M
α
CB
XB
x1
x2
x3
x4
x5
x6
-M
x5
10
[2]
1
-5
-1
1
0
5
-M
x6
7+t
1
1
1
0
0
1
7+t
-z
2+3M
-5+2M
3-4M
M
0
0
57t,即t2
cj
b
2
-5
3
0
-M
-M
α
CB
Xb
x1
x2
x3
x4
x5
x6
2
x1
5
1
1/2
-5/2
-1/2
1/2
0
-
-M
x6
2+t
0
1/2
[7/2]
1/2
-1/2
1
4/7+2t/
7
-z
0
-6+M/
2
8+7M/
2
1+
M/2
-M/2-
1
0
cj
b
2
-5
3
0
-M
-M
α
CB
Xb
x1
x2
x3
x4
x5
x6
2
x1
45/7+5t
/7
1
6/7
0
-1/7
1/7
5/7
3
x3
4/7+2t/
7
0
1/7
1
1/7
-1/7
2/7
-z
0
-50/7
0
-1/7
-M+1/
7
-M-16/
7
455t42tT10216t
此时最优解为(,0,),目标函数最大值为z
777
很明显当扩大第二项约束时最有利。
3、已知线性规划问题:
(2000,2004)
Minz2x1x22x3
x1x2x34
s.t.x1x2kx36
x10,x20,x3无约束
***
其最优解为:
x15;x20;x31
(1)写出该问题的对偶问题,并求出对偶问题的最优解;
(2)求出k的值
解:
(1)
Maxw4y16y2
y1y22
y1y21
s.t.
y1ky22
y1无约束,y20
由zw及互补松弛性质得
y1y22
4y16y212
得到y10,y22,得到k=1.
4、设有线性规划问题(2002)
Minz2x12x24x3
s.t.
2x1
3x1
3x25x32
x27x33
x14x26x35
x20,x30,x1无约束
试求
(1)该问题的对偶问题
2)写出该问题的标准型,并写出单纯性法求解的初始单纯型表。
解:
Maxw2y13y25y3
2y13y2y32
3y1y24y32
s.t.
5y17y26y34
y10,y20,y3无约束
Maxw2y13y25(y4y5)0y60y7My8My9
2y13y2y4y5y82
3y1y24(y4y5)y6y92
s.t.
5y17y26(y4y5)y74
y1,y2,y4,y5,y6,y70
5、设有线性规划问题:
(2002)
MaxZ2x14x2x3x4
x13x2x48
2x1x26
s.t.x2x3x46
x1x2x39
xj0,(j1,2,3,4)
T
已知该问题的最优解为:
X*[2,2,4,0]T,试根据对偶理论直接求出其对偶问题的最优解。
解:
对偶问题为
MinW8y16y26y39y4
y12y2y42
3y1y2y3y44
s.t.y3y41
y1y31
yi0(i1,2,3,4)
*
由互补松弛性得y40,y1y31,8y16y26y316,y31
解的y10,y25/3,y31,y40
四、指派问题
1、一个公司要分派5个推销员去5个地区推销某种产品,5个推销员在各个地区推销这种
产品的预期利润如下表所示,问应如何分派这
5个推销员才能使得公司总的利润最大。
(2003,2005)
ABCDE
甲1510121012
乙1112999
丙1020151713
丁18179913
戊713101312
解:
引入变量xij,并令
1当第i个推销员去第j个地区推销产品
xij0当第i个推销员不去第j个地区推销产品
则该问题的数学模型为:
maxzcijxij
xij1,j1,2,...,5
xij1,i1,2,...,5
xij1或0
该模型的目标函数可变化为
minzbijxij
xij1,j1,2,...,5
xij1,i1,2,...,5
xij1或0
其中bij20cij。
然后采用匈牙利法求解。
10
10
85
11
11
11
(bij)
10
10
10
10
10
10
10
1、
分配甲乙丙丁四个人去完成五项任务,每人完成各项任务的时间如下表所示,由于任务
数多于人数,故规定其中一人可兼完成两项任务,其余三人每人完成一项,试确定总花
费时间最小的指派方案。
(2001,2004)
A
B
C
D
E
甲
35
39
41
52
47
乙
49
48
36
30
43
丙
44
37
38
50
42
丁
34
52
46
33
55
五、非线性规划问题
1、设有如下的非线性规划问题:
(2000,2004,2009)
22
Minf(X)(x12)(x21)2
2
g1(X)x2x10
s.t.
g2(X)2x1x20
(1)用图解法求上述问题的最优解
(2)简述库恩-塔克条件,并用
(1)的结果说明其几何意义
2(x12)
2(x21)
2x1
1
1
解:
f(X)
g1(X)
g2(X)
2(x12)2x11
r1r20
2(x21)1121
22r1x1r240
2x22r1r20
2
r1(x2x1)0
r2(2x1x2)0
r1,r20
解得
r1r22/3,x1x21
2、试用动态规划方法求解下面的非线性规划问题(2001,2000)
10
Minf(Z)xi2
11
10
xi16
s.t.i1
xi0,(i1,2,...,10)
解:
具体计算过程参考p207或p208
f1s12
f22s22/3
f33s22/4
f1010s120/1010*161/510*24/5
六、简答及建模问题(新的题型方向)
简答题
1.简述对偶问题的对称性定理、弱对偶性定理、对偶定理。
对称性定理:
对偶问题的对偶是原问题。
弱对偶性定理:
若X是原问题的可行解,Y是对偶问题的可行解,则存在CX≦
Yb。
对偶定理:
若原问题有最优解,那么对偶问题也有最优解;且目标函数数值相等。
2.为什么排队论中假定顾客到达服从泊松发布,而服务时间服从负指数分布?
顾客到达服从泊松分布:
(1)在不相重叠的时间区间内顾客到达数是相互独立的(顾客到达是随机的)
(2)对充分小的t,在时间区间[t,tt)内有一个顾客到达的概率与t无关,
而约与区间长t成正比;
(3)对于充分小的t,在时间区间[t,tt)内有两个或两个以上顾客到达的概
率极小,以至于可以忽略。
这三个条件是符合实际情况的,由此推出的概率分布为泊松分布。
服务时间服从负指数分布:
对一顾客的服务时间定义为在忙期相继离开系统的两
顾客的间隔时间。
相继到达相继离开的间隔时间与输入过程为泊松流是一致的,
可以推出为独立且同负指数分布。
3.概括中国邮递员问题的解决思路:
问题是:
在一个有奇点的图中,要求增加一些重复边,使新图不含奇点,并且重复边的总权为最小。
思路:
找奇点,增加重复边,确定第一个可行方案;调整方案,去掉偶数条重复边,使重复边总权下降到最小。
二分析解答题
1.设备更新问题(动态规划)
某车间生产过程中必须使用某台设备,每年年初,车间领导决定是购置新设备还
是通过维修继续使用旧设备。
若购置新设备,需支付购置费,购买单价如下表第
二行所示,旧设备报废无残值;设备在使用的生命周期内每年需支付一定的维修
费用,且年度维修费用随着设备使用年限的增长而增长,如下表第四行所示。
请
制定2011-2015年的设备更新计划,使得总费用最小。
(忽略货币的时间价值)
答案:
{1,0,1,0,0}
(1,12)
2.报童通过订购报纸进行零售以获利。
已知,报童订购报纸的单位成本为c,
销售单价p,若报纸未卖出,则低价处理的单价为q。
已知pcq。
根据
过去的售卖经验得知,报童每日卖出r份报纸的概念为P(r)。
请问,为使得
收益最大化,报童每天的最佳订购量Q为多少?
答案:
记报童每天购进n份报纸时的平均收入为G(n),如果这天的需求量r≤n,
则他售出r份,退回n-r份;如果这天的需求量r>n,则n份将全部售出.考虑
到需求量为r的概率是f(r),所以
n
G(n)abrbcnrfrabnfr1r0rn1
问题归结为在f(r),a,b,c已知时,求n使G(n)最大.
通常需求量r的取值和购进量n都相当大,将r视为连续变量更便于分析和
计算,这时概率
f(r)转化为概率密度函数p(r),
(1)式变成
计算
式又可表为
用P1,P2分别表示曲线p(r)下的两块面积,则(3)式可记作
P1ab5
P2bc
a-b与退回一份赔b-c之比.显然,当报童与报社签订的合同
使报童每份赚钱和赔钱之比越大时,报童购进的份数就应该越多
3.某投资公司邀请你出资一万元参加如下游戏,游戏规则如下:
首先,提供给
你100万元的原始资本,该游戏分为50轮。
在每一轮中,盈利与亏损的可
能性都为50%。
若盈利,净盈利额为投资额的1.6倍;若亏损,净亏损额为
投资额的全部。
为保证游戏可持续进行,每轮游戏以当时总资产的一半作为
投资额,请问:
(1)你的期望收益大约是多少?
(2)你是否愿意参加此游
戏?
答案:
设xt为第t轮的初始资金,则
xt10.5xt0.5xt*1.6*0.50.9xt
那么,游戏结束50轮时期望收益为
50
x51(0.9)50*1000.0052*100=0.521
不愿意
为w。
因此,电站将灵活调整各个发电机组的开关状态,以实现发电能力与需求
的匹配。
此外,工程师告知,对于任一机组,一旦开动,在p小时内不得关闭;
而一旦关闭,在q小时内不得重新启动。
请问,如何决定各个机组在各个时点的开闭状态,以实现最小浪费。
答案:
设xit为第i个机组t时段的发电状态,则
0,关闭
xit
it1,开启
那么
24N
minzw*(xit*SiD1D2D3)
t0i1
t1N
s.t.xit*SiD1;
t0i1
t2N
xit*SiD2;
tt1i1
24N
xit*SiD3;
tt2i1
xitxit1xie,et1,K,mintp,24,i1,K,N;
xit1xit1xie,et1,K,mintq,24,i1,K,N;
xit0,1,i1,K,N,t1,K,24.