第四章平面图.docx

第四章平面图.docx

《第四章平面图.docx》由会员分享，可在线阅读，更多相关《第四章平面图.docx（26页珍藏版）》请在冰豆网上搜索。

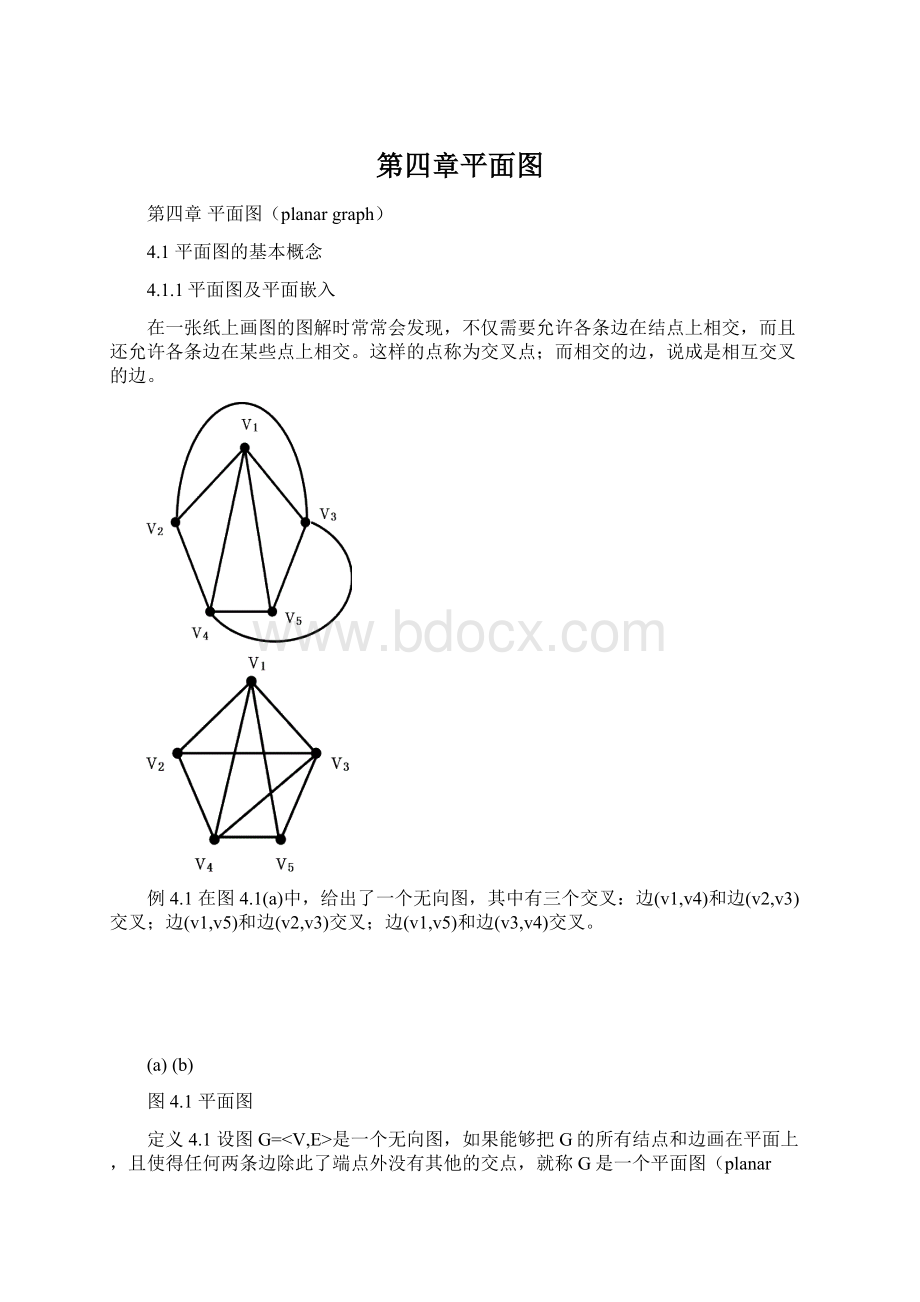
第四章平面图

第四章平面图（planargraph）

4.1平面图的基本概念

4.1.1平面图及平面嵌入

在一张纸上画图的图解时常常会发现，不仅需要允许各条边在结点上相交，而且还允许各条边在某些点上相交。

这样的点称为交叉点；而相交的边，说成是相互交叉的边。

例4.1在图4.1（a）中，给出了一个无向图，其中有三个交叉：

边（v1,v4）和边（v2,v3）交叉；边（v1,v5）和边（v2,v3）交叉；边（v1,v5）和边（v3,v4）交叉。

（a）（b）

图4.1平面图

定义4.1设图G=是一个无向图，如果能够把G的所有结点和边画在平面上，且使得任何两条边除此了端点外没有其他的交点，就称G是一个平面图（planargraph）。

或称G可嵌入平面S。

若G可嵌入平面，则称G是可平面图。

画出的无边相交的图称为G的平面嵌入（drawninaplane）。

无平面嵌入的图称为非平面图（nonplanar）。

Definition:

agraphcanbedrawninaplanesothatnoedgescrossexceptatvertices.

例4.2对于图4.1（a）中和无向图来说，将此图的图解重新画之后，它不包含任何交叉，如图4.1（b）所示。

因此，给定的图是一个平面图。

例4.3K1（平凡图），K2，K3，K4都是平面图，其中，K1，K2，K3本身就已经是平面嵌入，K4的平面嵌入为图4.2中（4）所示。

K5－e（K5删除任意一条边）也是平面图，它的平面嵌入可表示为图4.2中（5）。

完全二部图K1,n（n≥1）,K2,n（n≥2）,也都是平面图，其中标准画法画出的K1,n已经是平面嵌入，K2,3的平面嵌入可由图4.2中（6）给出。

图4.2中

（1），

（2），（3）分别为K4,K5－e,K2,3的标准画法。

图4.2可平面化图

例4.4图4.3（a）所示的立方体是否可平面化？

.

（a）（b）（c）

图4.3可平面化立方体

解：

图4.3（a）的图解包括有交叉边。

它对它的图解难重新画之后，没有任何两个边是交叉的。

因此它是可平面的。

见图4.3（b）和（c）.

将结点和边画成彩色的可清楚地看出平面嵌入。

设G=是能够画于平面上的图解中的无向图，并且设

C=v1…v2…v3…v4…v1是图中的任何基本循环。

此外，设x=v1…v3和x′=v2…v4是图中的任意两条不交叉的基本路径。

在图4.4中，给出了两种可能的结构。

显然，当且仅当x和x′或者都在基本循环C的内部，或者都在基本循环C的外部，G才是个非平面图，因为这时基本路径x和x′是相互交叉的。

判断一个图是非平面图时，上面的性质甚为有效。

图4.4

例4.5设有一个电路，它含有两个结点集V1和V2，且

=3。

用导线把一个集合中的每一个结点，都与另外一个集合中的每一个结点连通，如图所示。

试问，是否有可能这样来连线，使得导线相互不交叉？

图4.5

解：

这个问题等价于判断图4.5是否是个平面图。

可以看出，给定图中有一个基本循环C=v1v6v3v5v2v4v1，如图4.6（a）所示。

试考察三条边（v1,v5）,（v2,v6）和（v3,v4）。

上述的边中的每一条，或者处于C的内侧，或者处于C的外侧。

显然，三条边中至少有两条边必定处于C的同一侧，因此避免不了交叉，如图4.6（b）所示。

故给定图是非平面图。

（a）（b）

图4.6

在研究平面图理论中居重要地位的两个图，这就是完全图K5和完全二部图K3,3，它们都不是平面图。

图4.7

还有两个非常显然的事实，用下面定理给出。

定理4.1若图G是平面图，则G的任何子图都是平面图。

　由定理4.1立刻可知，Kn（n≤4）和K1,n（n≥1）的所有子图都是平面图。

定理4.2若图G是非平面图，则G的任何母图也都是非平面图。

母图：

设G=，G'=为两个图（同为无向图或同为有向图），若V'

V且E'

E，则称G'是G的子图，G为G'的母图

推论Kn（n≥5）和K3,n（n≥3）都是非平面图。

　　本推论由K5，K3,3不是平面图及定理4.2得证。

　　还有一个明显的事实也用定理给出。

定理4.3设G是平面图，则在G中加平行边或环后所得图还是平面图。

　　本定理说明平行边和环不影响图的平面性，因而在研究一个图是否为平面图时可不考虑平行边和环。

4.1.2平面图的面与次数

定义4.2设G是一个连通平面图（且已是平面嵌入），由图中的边所包围的区域称为G的一个面（face），包围该面的诸边所构成的回路称为这个面的边界（boundary）。

例4.5图4.8具有6个结点和9条边，它把平面划分成五个面。

其中r1,r2,r3,r4四个面是由回路构成边界，如r1由回路badb所围，r2由回路bdcb所围，,r3可看作从点c开始围绕,r3按反时针方向，得到一个回路cdefec所围。

另外还有一个面r5在图形之外，不受边界约束，称作无限面。

图4.8

规定：

面的边界的回路长度称作是该面的度数（degreeofaplane），记为deg（r）。

例如图4.8中，deg（r1）=3,deg（r2）=3,deg（r3）=5,deg（r4）=4，deg（r5）=3

定理4.4一个有限平面图，面的次数之和等于其边的两倍。

证明：

因为任何一条边，或者是二个面的公共边，或者在一个面中作为边界被重复计算两次，故面的次数之和等于其边数的两倍。

例4.8图中，

，正好是边数的两倍。

4.1.3极大平面图及性质

定义4.3设G为简单平面图，若在G的任意不相邻的顶点u，v之间加边（u，v），所得图为非平面图，则称G为极大平面图。

　　从定义不难看出，K1，K2，K3，K4，,K5-e（K5删除任意一条边）都是极大平面图。

还可以容易地证明下面两个定理。

定理4.5极大平面图是连通的。

定理4.6设G是n（n≥3）阶极大平面图，则G中不可能存在割点和桥。

　　极大平面图的特点由下面定理给出。

定理4.7设G为n（n≥3）阶简单连通的平面图，G为极大平面图充分必要条件是：

（1）G的每个面的次数均为3.

（2）设G有m条边r个面，则3r=2m。

（3）设G有n个顶点，m条边和r个面，则m=3n-6，r=2n-4

例4.5在图4.9所示的各平面图中，只有（3）是极大平面图。

图4.9

4.1.4、极小非平面图

定义4.4若在非平面图G中任意删除一条边，所得图为平面图，则称G为极小非平面图。

　　可以验证，K5和K3,3都是极小非平面图。

4.2欧拉公式

4.2.1欧拉公式及其推广

　　欧拉在研究多面体时发现，多面体的顶点数减去棱数加上面数等于2。

后来发现，连通的平面图的阶数，边数，面数之间也有同样的关系。

定理4.8（欧拉公式）对于任意的连通的平面图G，有

n-m+r=2

其中，n，m，r分别为G的顶点数，边数和面数。

例如下图中，r=4,n=6,m=8,则n-m+r=6-8+4=2

图4.10

证对边数m作归纳法。

（1）m＝0时，由于G为连通图，所以G只能是平凡图，则有n=1，m=0，r=1，结论成立。

（2）若m=1,即n=2,m=1,r=1,则n-m+r=2,结论成立。

（3）设m＝k（k≥1）时欧拉公式成立。

即n'-m'+r'=2。

证明当m＝k+1时，结论也成立。

对G进行如下讨论。

因为G是连通的，在有k条边的连通图上增加一条边，仍为连通图。

于是有下面两种情况：

　　①若G是树，则在G中加一条边使G仍为树。

见图4.11（a）。

此时，G的点数和边数各增加了1，而面数没变。

即m=m'+1,n=n'+1，r=r'。

由归纳假设可知

n'-m'+r'=2

于是

n-m+r=（n'+1）-（m'+1）+r'=n'-m'+r'=2

　　②若G不是树，则G中含回路。

用一条边连接图上的两个已知点u和v，如图4.11（b）所示。

此时，边数和面数都增加了1,而结点数没变。

即m=m'+1，n'=n，r'=r-1，由归纳假设有

n'-m'+r'=2

于是:

n-m+r=n'-（m'+1）-（r'+1）=n'-m'+r'=2结论成立。

（a）（b）

图4.11

欧拉公式中，平面图G的连通性是不可少的。

对于非连通的平面图有下面定理成立。

欧拉公式常用来判断一个图是非平面图。

例4.6证明K3,3是非平面图。

证：

假设K3,3是平面图。

则图中的任何一个回路至少有4条边，作为面的边界的边至少是4r。

而在平面图中，任何一条边至多是两个回路的边界。

因此有：

2m≥4r

应用欧拉公式：

n-m+r=2得：

2m≥4（m-n+2）

对于K3,3，m=9,n=6代入上式：

18≥4（9-6+2）=20矛盾

所以，K3,3不是平面图。

同理可证K5不是平面图。

定理4.9（欧拉公式的推广）对于具有k（k≥2）个连通分支的平面图G，有

n-m+r=k+1

其中n，m，r分别为G的顶点数，边数和面数。

　　证设G的连通分支分别为G1，G2，…，Gk，并设Gi的顶点数，边数，面数分别为ni，mi，ri，i=1，2，…，k.由欧拉公式可知:

ni-mi+ri=2，i=1，2，…，k（4.1）

易知，m=

，n=

，由于每个Gi有一个外部面，而G只有一个外部面，所以

G的面数r=

-k+1,于是，对（4.1）的两边同时求和得

2k=

（ni-mi+ri）

=

ni-

mi+

ri

=n-m+r+k-1

经过整理得

n-m+r=k+1

　　将定理4.9称为欧拉公式的推广。

由欧拉公式及其推广可以得到平面图的另外一些性质。

4.2.2平面图的边数m与顶点数n的关系

定理4.10设G是连通的平面图，且每个面的次数至少为l（l≥3），则G的边数m与顶点数n有如下关系：

m≤

（n－2）

　　由定理4.4可知:

2m=

deg（Ri）≥l·r　（4.2）

由欧拉公式可知:

r=2+m-n　（4.3）

将（4.3）代入（4.2）得

2m≥l（2+m-n）

经过整理得:

m≤

（n－2）

推论K5与K3,3都不是平面图。

　　证若K5是平面图，由于K5中无环和平行边，所以每个面的次数均大于或等于l≥3，由定理4.10可知边数10应满足

10≤

（5-2）=9

这是个矛盾，所以K5不是平面图。

　　类似地，若K3,3是平面图，由于K3,3中最短圈的长度为l≥4，于是边数9应满足

9≤

（6-2）=8

这又是矛盾的，所以K3,3也不是平面图。

利用欧拉公式的推广形式容易证明此定理。

而对于有k个连通分支的平面图，边数与顶点之间的关系可由下列定理给出。

定理4.11设G是有k（k≥2）个连通分支的平面图，各面的次数至少为l（l≥3），则边数m与顶点数n应有如下关系：

m≤

（n-k-1）

证明略。

定理4.12设G是n（n≥3）阶m条边的连通平面图，则

m≤3n-6

证由于G是连通平面图，又因为n≥3，故对图G中的每个面来说，deg（ri）≥3,因而有：

2m=

再由欧拉公式:

n-m+r=2

3n-3m+3r=6

3n-6=3m-3r≥3m-2m=m即m≤3n-6证毕。

定理4.13若G是连通的简单平面图，则

。

证明：

用反证法。

若

，则有6n≤2m，即3n≤m，由定理4.12，有3n≤3n-6,矛盾。

4.3平面图的判断

虽然欧拉公式有时能用来判定某一个图是非平面图，但是还没有简便的方法可以确定某个图是平面图。

4.3.1库拉托夫斯基定理

为了讨论平面图的判别法，还需要给出下面两个定义。

在图4.12中，给出了两个图解。

如图4.12（a）所示，试往图中的一条边上，插入一个新的次数为二的结点，把一条边分解成两条边，则不会改变给定图的平面性。

另外，如图4.12（b）所示，把联系于一个次数为二的结点的两条边，合并成一条边，也不会改变给定图的平面性。

（a）（b）

图4.12

定义4.5设G1和G2是两个无向图，如果图G1与G2同构，或通过反复插入或消去2度顶点后是同构的，则称G1与G2是同胚（homeomorphic）。

例如：

在图4.13中，

（1）与K3同胚,

（2）与K4同胚。

图4.13

在具体使用时，常用边压缩方法。

定义4.6图G的一个边压缩为：

将图G中的两个邻接顶点vi，vj及边（vi,vj）压缩成一个顶点，可用一个新的符号w代替，使它邻接于vi,vj的顶点。

一个G可压缩到图H是指G经过一系列压缩后得到H。

例如：

边压缩的例子。

图4.14

图4.15

定理4.14（库拉托夫斯基定理）图G是平面图当且仅当G中既不含与K5同胚子图，也不含与K3,3同胚子图。

本定理的证明略。

对等定理：

图G是平面图当且仅当G中不含经过边的压缩能成为K5和K3,3的子图。

例4.7证明彼得松图不是平面图。

　　证明：

方法1用G表示彼得松图，令

G'=G-{（j,g），（c,d）}

G'如图4.16（3）所示，易知它与K3,3同胚，由库拉托夫斯基定理可知，G为非平面图。

图4.16

方法2：

用G表示彼得松图，如图4.17

（1）所示。

将此图中的绿边压缩掉，得图4.17

（2），显然，图4.17

（1）与图4.17

（2）同胚。

而图4.17

（2）为K5，是非平面图，由库拉托夫斯基定理可知，G为非平面图。

（1）

（2）

图4.17

4.4平面图的对偶图

4.4.1平面图的对偶图

定义4.7设G是连通平面图，且G有k个面F1,F2,…Fk（包括外部面）构造G的对偶图G*如下：

（1）在G的每个面内设置一个结点vi*（1

）。

（2）过Fi与Fj的每一条公共边e，作一条仅作一条e*＝（vi*，vj*）（1

）与e相交，e*不与其它任何边相交。

（3）若e为G中的桥且在面Fi的边界上，则e*是以Fi中G*的顶点vi*为端点的环，即e*＝（vi*，vi*）.

从定义不难看出G的对偶图G*有以下性质：

1.G*是平面图，而且是平面嵌入。

2.G*是连通图。

3.若边e为G中的环，则G*与e对应的边e*为桥，若e为桥，则G*中与e对应的边e*为环。

4.在多数情况下，G*为多重图（含平行边的图）。

5.同构的平面图（平面嵌入）的对偶图不一定是同构的。

　　图4.18中

（1），

（2）所示的图（黑线边的图）是同构的，但它们的对偶图不是同构的。

图4.18

4.4.2对偶图的性质

平面图G与它的对偶图G*的顶点数，边数和面数有如下定理给出的关系。

定理4.15设G*是连通平面图G的对偶图，n*，m*，r*和n，m，r分别为G*和G的顶点数，边数，面数，则

（1）n*＝r

（2）m*＝m

（3）r*＝n

（4）设G*的顶点vi*位于G的面Ri中，则dG*（vi*）＝deg（Ri）.

　　证:

由G*的构造可知，

（1），

（2）是显然的。

　　（3）由于G与G*都连通，因而满足欧拉公式:

n-m+r=2　

n*-m*+r*=2　

由

（1），

（2）及上而两式可知

r*=2+m*-n*=2+m-r=n

（4）设G的面Ri的边界为Ci，设Ci中有k1（k1≥0）条桥，k2个非桥边，于是Ci的长度为k2+2k1，即deg（Ri）＝k2+2k1，而k1条桥对应vi*处有k1个环，k2条非桥边对应从vi*处引出k2条边，所以dG*（vi*）＝k2+2k1＝deg（Ri）.

说明：

对于非连通的平面图，此性质不成立。

例。

4.4.3自对偶图

定义4.8设G*是平面图G的对偶图，若G*

G，则称G为自对偶图。

例4.9　在图4.19

（1），

（2），（3）中黑线边图都是自对偶图。

图4.19

回路图（圈图）：

由n个顶点和n个顶点依次成边所构成的基本回路图。

分奇圈图和偶圈图。

轮图：

在n-1（n≥4）边形Cn-1内放置一个顶点，使这个顶点与Cn-1上的所有顶点均相邻。

所得n阶简单图称为n阶轮图。

n为奇数的轮图称为奇阶轮图，n为偶数的轮图称为偶阶轮图，常将n阶轮图记为Wn。

图4.19（3）中，黑边图为奇阶轮图W5。

可以证明轮图都是自对偶图。

4.5平面图的着色

图着色问题的研究起源于四色猜想，也称作四色问题。

是世界近代三大数学难题之一。

四色问题的内容是：

任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。

用数学语言表示，即：

将平面任意地细分为不相重迭的区域，每一个区域总可以用1，2，3，4这四个数字之一来标记，而不会使相邻的两个区域得到相同的数字。

如下图：

图4.20

着色问题包含点着色，边着色，平面图的面着色等。

统称为染色图（colouringGraph）。

4.5.1点着色

规定点着色都是对无环无向图进行的。

定义4.9对无环图G的每个顶点涂上一种颜色，使相邻的顶点涂不同的颜色，称为对图G的一种着色。

若能用k种颜色给G的顶点着色，就称对G进行了k着色，也称G是k-可着色的。

若G是k-可着色的，但不是（k-1）-可着色的，就称G是k色图，并称这样的k为G的色数，记作χ（G）=k。

对于点着色，有以下一些性质：

1.χ（G）=1当且仅当G是零图。

2.

（Kn）=n.

3.偶回路的色数为2，奇回路图和奇阶轮图的色数均为3，而偶阶轮图的色数为4.

4.设G中至少含一条边，则

（G）=2当且仅当G为二部图.

注：

本性质中加G中至少含一条边的条件，是为了去掉零图这种特殊的二部图

定理4.16对于任意的无环图G，均有

（G）≤Δ（G）+1

证明：

考虑到完全图G的色数：

（G）=Δ（G）+1。

从完全图是删去一些边不会使正常顶点的着色数增大。

事实上，删去一些边后对完全图的正常着色不会改变，即原来完全图上的着色也是删除边后所得子图的一种正常着色，所以对任意图G，有：

（G）≤Δ（G）+1证毕。

当图G既不是完全图也不是奇圈图时，定理4.16给出的色数的上界可以改进。

定理4.17设连通图G不是完全图Kn（n≥3）,也不是奇回路图，则

χ（G）≤Δ（G）

本定理的证明略。

本定理称为布鲁克斯（Brooks）定理。

例4.10求下面所示各图的色数。

图4.21

解为方便起见，记图4.19中的4个图依次的为G1，G2，G3（彼得松图）和G4.

（1）G1为二部图，由性质4可知，

（G1）=2.

（2）G2为6阶轮图W6，由性质3可知，

（G2）=4.

（3）G3是彼得松图。

由于Δ（G3）=3，利用布鲁克斯定理可知：

（G3）≤3，又因为G3中有奇回路，由性质3知，χ（G3）≥3，于是

（G3）=3.

（4）由布鲁克斯定理可知，

（G4）≤Δ（G4）=4，又因为G4中有奇回路，于是

（G4）≥3，因而

（G4）为3或4。

讨论：

用用3种颜色还是4种颜色给图G4着色？

为此，我们给出WelchPowell着色法。

（1）将图中的顶点度数按递减次序排列。

（2）用第一种颜色对第一个点着色，并且按排列次序，对与前面着色点不邻接的每一个点着上同样的色。

（3）用第二种颜色对尚未着色的点重复

（2），用第三种颜色继续这种做法，直到所有的点都着上色为止。

因此，用3种颜色不可能给G4着色，于是只能是

（G4）=4.

4.5.2地图及其面着色、面色数

连通无桥平面图的平面嵌入及其所有的面称为平面地图或地图，地图的面称为“国家”。

若两个国家的边界至少有一条公共边，则称这两个国家是相邻的。

定义4.10对地图G的每个国家涂上一种颜色，使相邻的国家涂不同的颜色，称为对G的一种面着色，若能用k种颜色给G的面着色，就称对G的面进行了k着色，或称G是k-面可着色的。

若G是k-面可着色的，但不是（k-1）-面可着色的，就称G的面色数为k，记作

*（G）=k.

　　研究地图的着色可以转化成对它的对偶图的点着色，见下面定理。

定理4.18地图G是k-面可着色的当且仅当它的对偶图G*是k-可着色的。

　　证必要性。

给G一种k-面着色。

由于G连通，由定理4.15可知，n*＝r，即G的每个面中含G*的一个顶点，设vi*位于G的Ri内，将G*的顶点vi*涂Ri的颜色，易知，若vi*与vj*相邻，则由于Ri与Rj的颜色不同，所以vi*与vj*的颜色也不同，因而G*是k-可着色的。

类似地可证充分性。

由定理4.18可知，研究地图的着色（面着色），等价于研究平面图的点着色。

对于平面图的点着色问题，到目前为止，人们从数学上证明了五色定理，用计算机证明了四色定理。

定理4.19任何平面图都是5-可着色的。

（五色定理）

证明:

用数学归纳法对顶点作归纳假设证明。

设图G的顶点个数为n。

当n≤5时，定理成立。

假设对顶点数为n-1的平面图定理成立，下面证明对顶点数为n的图G，定理也成立。

设图G是n个顶点的简单平面图，则有

。

则图G中至少有一顶点v，其度数deg（v）≤5。

在图G中删除顶点v得到G’，由归纳假设，G’是5-可着色的。

现将v加入到G’中，有两种情况：

（1）如果deg（v）<5，则对v着以与其邻接的顶点不同的颜色。

（2）如果deg（v）=5，即v与G’中5个顶点相邻，但5顶点中有重复颜色，v可以用第五种颜色着色。

假设v与G’中5个点相邻，5顶点着色各不相同，设5个顶点分别是a，b，c，d，e。

见图4.22

（1）。

设在G’中，顶点a与c之间是一条其顶点用红色（r）和黄色（y）交替着色的通路，这条通路与v形成一条回路，组成一个面。

b在这个面的内部或在外部。

见图4.22

（2）。

如果同样b，d；c，e；c，e；b，e；a，d都有一个这样交替着色的通路，相互交叉。

这时a，b1，b2，b3，b4，b5组成一个K5。

与G是平面图矛盾。

这是不可能的。

即然b，d之间不存在交替着色的通路，我们就可以对G’中与顶点b用另外两种颜色，比如说是白色（w）和绿色（g）着色而形成有通路中，交换其颜色。

这种交换不会影响G’中其它各顶点的着色。

这样，可以将顶点v着成白色。

如果顶点a与顶点c之间不存在两种颜色交替着色的通路，则可将顶点a和顶点c着成同一种颜色，顶点子v则可着成另一种颜色。

总之，无论是那种情况，都可对图G进行5-可着色。

（1）

（2）

图4.22

4.5.3边着色及边色数

　定义4.11对图G的每条边涂上一种颜色，使相邻的边涂不同的颜色，称为对图G边的一种着色。

若能用k种颜色给G的边着色，就称G是k-边可着色的。

若G是k-边可着色的，但不是（k-1）-边可着色的，就称k是G的边色数，记作χ'（G）=k.

关于边着色，有一个重要的定理，就是维津定理.

定理4.20设G是简单图，则Δ（G）≤χ'（G）≤