《自动控制原理》作业习题docxWord文档下载推荐.docx
《《自动控制原理》作业习题docxWord文档下载推荐.docx》由会员分享,可在线阅读,更多相关《《自动控制原理》作业习题docxWord文档下载推荐.docx(25页珍藏版)》请在冰豆网上搜索。
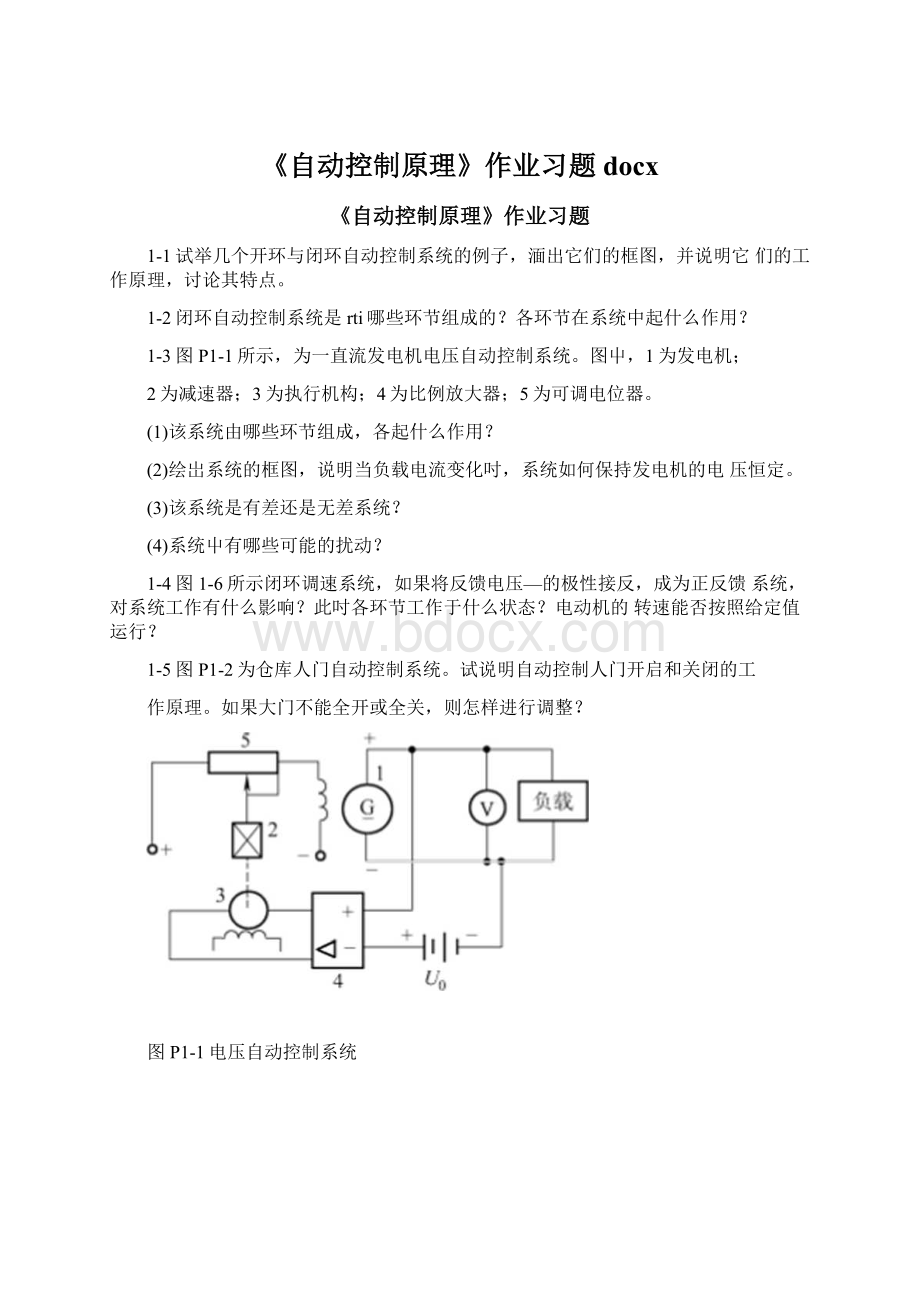
2-7已知一系统由如下方程组组成,试绘制系统方框图,并求出闭环传递函数。
X|($)=X「($•)%($)-叫(5)[旳($)-必G)]XcG)
X2(5)=W2(5)[X1(5)-VV6(5)X3(5)]
X3(f)=[X2(0-Xc(s)W5(S)]W3($)
Xc«
"
(s)X3($)
8试分别化简图P2-7和图P2-8所示的结构图,并求岀相应的传递函数。
图P2-9
2-10求如图P2-10所示系统的传递函数。
图P2-10
2-11求图P2-11所示系统的闭环传递函数。
12图P2-12所示为一位置随动系统,如果电机电枢电感很小可忽略不计,并且不计系统的负载和粘性摩擦,设~=0海,/仃=0久,其中外、久分别为位置给定电位计及反馈电位计的转角,减速器的各齿轮的齿数以叫表示Z。
试绘制系统的结构图并求系统的传递函数:
3-
图P2-13
2-14画出图P2-14所示系统的信号流图,并分别求出两个系统的传递函数
图P2-14
4-1一单位反馈控制系统的开环传递函数为WK($)=,r。
求:
(1)系统的单位阶跃响应及动态特性指标6%、5、ts、
(2)输入量X「(t)二t时,系统的输出响应;
(2)输入量x「(t)为单位脉冲函数时,系统的输岀响应。
4-2一单位反馈控制系统的开环传递函数为=其单位阶跃响应曲
$(窈+1丿
线如图P3-1所示,图中的X尸1.25,U=1.5s。
试确定系统参数《及t值。
图P3-1
3-3一单位反馈控制系统的开环传递函数为”k(s)=―。
已知系统的xr
击+2宓)
(t)二1(t),误并时间函数为曲)=1.4厂川一0.4厂帧,求系统的阻尼比歹、口然
振荡角频率妁、系统的开坏传递函数和闭坏传递函数、系统的稳态误差。
3-4已知单位反馈控制系统的开环传递函数为叭($)=丁»
,试选择心及t值以S[TS+1)
满足下列指标。
当Xr(t)二t吋,系统的稳态误差e(00)W0.02;
当Xr(t)二1(t)时,系统的B%W30%,ts(5%)WO.3s。
3-5已知单位反馈控制系统的闭环传递函数为WB(S)=-—金——,试画出以
®
为常数、孑为变数时,系统特征方程式的根在S复平面上的分布轨迹。
3-6一系统的动态结构图如图P3-2所示,求在不同的Kk值下(例如,KfI、反=3、心二7)系统的闭环极点、单位阶跃响应、动态指标及稳态误弟。
图P3-2
3-7一闭环反馈控制系统的动态结构图如图P3-3所示。
(1)求当6%W20%、ts(5%)=1.8s时,系统的参数&
及工值°
(2)求上述系统的位置误差系数心、速度误差系数K、.、加速度误差系数K“及其相应的稳态误差。
图P3-3
3-8一系统的动态结构图如图P3-4所示。
求
(1)s=0,乃=0.1时,系统的/%、/$(5%)
(2)巧=0.1,了2=0时,系统的/%、.(5%)
(3)比较上述两种校止情况下的暂态性能指标及稳态性能。
图P3-4
3-9如图P3-5所示系统,图中的叫(Q为调节对象的传递函数,肥(s)为调节器的传递函数。
如果调节对象为叫(g:
T,>
T2,系统要求的指标
(斤$+1人7號+1丿
为:
位置稳态误并为零,调节时间最短,超调量6%W4.3%,问下述三种调节器中哪一种能满足上述指标?
其参数应具备什么条件?
三种调节器为(a)Wc(s)=Kp;
(b)叱心)=心_^^;
(c)W()=K“((:
:
;
))。
图P3-5
3-10有闭环系统的特征方程式如下,试用劳斯判据判断系统的稳定性,并说明特征根在复平而上的分布。
(1)53+20.y2+45+50=0
(2)53+2()524-45+100=0
(3)s4+2s3+6s2+8s+8=()
(4)2宀芒-15芒+25."
+2—7=()
(5)56+32+9宀肿+22“+12$+12=0
3-11单位反馈系统的开环传递函数为
(、氐(0.5$+1)
必心右+谕.5宀山)
试确定使系统稳定的反值范围。
3-12已知系统的结构图如图P3-6所示,试用劳斯判据确定使系统稳定的心值范围。
图P3-6
3-13如果采用图P3-7所示系统,问:
•取何值时,系统方能稳定?
3-14设单位反馈系统的开环传递函数为叫($匕(1+033』1+0167,)'
要求闭环特征根的实部均小于-1,求K值应取的范围。
图P3-7
(1)
(2)
3-15设有一单位反馈系统,如果其开环传递函数为
叫(S)=——?
——rs(s+4X5s+l)讥)—go」)八丿“(s+4X5s+l)
求输入量为xr(r)=r和xr(r)=2+4r+5r2时系统的稳态误差。
3-16有一单位反馈系统,系统的开坏传递函数为W,G)=Alo求当输入量为
S
心(/)=*2和xr(t)=sincot时,控制系统的稳态误并。
3-17有一单位反馈系统,其开环传递函数为肌(小=需号,求系统的动态误差系数;
并求当输入量为讪卜1+/+*2时,稳态误差的时间函数询。
乙
3-18一系统的结构图如图P3-8所示,并设必(.0=心(1十八0,晒(Q=丁斗。
S-5(1+T2S)
当扰动量分别以△"
($)=+、古作用于系统时,求系统的扰动稳态误差。
图P3-8
3-19一复合控制系统的结构图如图P3-9所示,其中K\=2K、=1,T2=0.25s,心二2。
(1)求输入量分别为xr(r)=l,xr(r)=r,xr(t)=^-t时,系统的稳态误差;
(2)求系统的单位阶跃响应,及其5%,.值。
图P3-9图P3-10
3-20一复合控制系统如图P3-10所示,图中Wc(s)=as2+bs,叫(小二——岁——o如果系统由1型提高为3型系统,求a值及b值。
gs(l+O」祖1+0・2$)
4-1求下列各开环传递函数所对应的负反馈系统的根轨迹。
<
1)Wk($)=
_K卫+3)
($+1)($+2)
K&
(f+5)
s($+3)($+2)
⑶WK(s)=
匕(s+3)
(s+1)($+5)($+10)
4-2求下列各开环传递函数所对应的负反馈系统的根轨迹。
兀($+2)
s~+2$+3
WK(s)=
KW+2)
s(s+3)($2+2s+2)
(5)
(4)
K卫+1)
S(S一1)(524-454-16)
WK(S)=
K/O.ls+1)
$($+1)(025$+1尸
4-3已知单位负反馈系统的开环传递函数为
[Vf=
K'
s(Ts+1)(52+2s+2)求当K=4时,以T为参变量的根轨迹。
4-4已知单位负反馈系统的开环传递函数为
K($+a)£
($+1)
求当K=丄时,以刃为参变量的根轨迹。
4
4-5已知单位负反馈系统的开环传递两数为
($+16)(/+2$+2)
试用根轨迹法确定使闭环主导极点的阻尼比§
=0.5和口然角频率
4-6已知单位正反馈系统的开环传递函数为
Wk(s)=
($+1)($—1)($+4)2
试绘制其根轨迹。
4-7设系统开环传递函数为
心($+1)s"
s+2)(£
+4)
试绘制系统在负反馈与正反馈两种情况下的根轨迹。
4-8设单位负反馈系统的开环传递函数为
K(s+1)
/(0」$+1)
如果要求系统的一对共轨主导根的阻尼系数为0.75,用根轨迹法确定
(1)串联相位迟厉环节•设匕=15。
(2)串联相位引前环节,设ka=15o
4-9已知单位负反馈系统的开环传递西数为
5(5+4)(5+20)
设耍求kv>
12(1/5).3%<
25%.ts<
0.75,试确处冷联引前校正装究的传递苗数,并绘制校正
前、后的系统根轨迹。
4-10设单位负反馈系统的开环传递函数为
叭($)=
s(s+4)($+5)
要求校正后人>
30(1/5)、主导极点阻尼比歹=0.707,试求串联迟后校正装汽的传递函数。
4-
11己知负反馈系统的开环传递函数为
要使系统闭环主导极点的阻尼比歹=0.5、自然振荡角频率血“=5、kv>
50(1/^)时,求串联迟后一
引前校正装置的传递函数,并绘制校正前、后的系统根轨迹。
5-1已知单位反馈系统的开环传递函数为
10
7+\
当系统的给定信号为
(1)xrl(r)=sin(r+30)
(2)xr2(t)=2cos⑵一45°
)
(3)xr3(r)=sin(/+3(T)—2cos⑵一45°
吋,求系统的稳态输出o
5-2绘出下列各传递函数对应的幅相频率特性o
(1)W(s)=肘"
&
=10,N=l、2)
(2)W(s)=1()
0.15±
l
(3)W(s)=KsN(K=10,N=1、2)
W($)=10(0.1$±
1)
(9)IV(5)=T252+2^+1@=0.707)
(10)W($)=2严$+1)
¥
+2$+1
5-3绘出习题5-2各传递函数对应的对数频率特性。
6-
4绘出下列系统的开环传递函数的幅相频率特性和对数频率特性。
5-
6设系统的开环幅相频率特性如图P5-1所示,写出开环传递函数的形式,判断闭环系统是否稳定。
图屮P为开环传递函数右半平面的极点数。
图P5-1
5-7已知最小相位系统开环对数幅频特性如图P5-2。
(1)写出其传递函数
绘岀近似的对数相频特性
图P5-2
5-8已知系统开环传递函数分别为
(1)叭⑶一$(0.25$+l)(0.06s+l)
试绘制波徳图,求相位裕量及增益裕量,并判断闭环系统的稳定性。
5-9设单位反馈系统的开环传递函数为
叭(s)=
当输入信号心⑴为5rad/s的止弦信号时,求系统稳态谋弟。
5-10已知单位反馈系统的开环传递函数,试绘制系统的闭环频率特性,计算系统的谐振频率及谐振峰值。
5-11单位反馈系统的开环传递函数为
7
5(0.0875+1)
试用频域和时域关系求系统的超调量5%及调节时间―
5-12己知单位反馈系统的开环传递函数为
5(0.15+1)(0.015+1)
作尼氏图,并求出谐振峰值和稳定裕量。
5-13如图P5-3所示为0型单位反馈系统的开环幅相频率特性,求该系统的阻尼比歹和自然振荡角频率。
图P5-3
7-
1设一单位反馈系统其开环传递函数为
若使系统的稳态速度误差系数kv=20r*,相位裕量不小于50。
,增益裕量不小于
10dB,试确定系统的串联校止装置。
2设一单位反馈系统,其开环传递函数为
求系统的稳态加速度谋差系数=10<
2和相位裕量不小于35。
时的出联校正装置。
6-3设一单位反馈系统,其开环传递函数为
Wk(沪丄
要求校止后的开环频率特性曲线与M=4dB的等Ml员|相切。
切点频率°
“=3,,并月.在高频段3>
200具有锐截止-3特性,试确定校正装置。
5-4设一单位反馈系统,其开环传递函数为
W(5)=c
$(0.2$+必0.5£
+1)
要求具冇相位裕量等于45。
及増益裕量等于6dB的性能指标,试分别采用串联引前校止和串联迟后校止两种方法,确定校止装置。
7-5设一随动系统,其开环传递函数为
如要求系统的速度稳态误差为10%,M“51.5,试确定申联校正装置的参数。
6-6设一单位反馈系统,其开环传递函数为
126
$(0.1$+1)(0.00166$+1)
耍求校正后系统的相位裕量兀0.)=40。
±
2。
,增益裕量等T10dB,穿越频率coe>
\radls,且开环增益保持不变,试确定串联迟后校正装置。
6-7采用反馈校正后的系统结构如图6—1所示,其中H(S)为校正装置,
~~T町(刖卜咽T旳(、)I~lI比⑴j
图6—1
”2(s)为校正对象。
要求系统满足下列指标:
稳态位置误差eU=0;
稳态速度
误差q,(oo
递函数。
)=0.5%;
/(6yJ>
45oo试确定反馈校正装置的参数,并求等效开环传
W]($)=200
必卜)-(o.ois+1X0.1$+1)
WK(^)=—
$
6-8一系统的结构图如题6-7,要求系统的稳态速度误差系数kv=200,
超调量〃%<
20%,调节时间ts<
2s,试确定反馈校止装置的参数,并绘制校正前、后的波德图,写出校正后的等效开环传递函数。
7-1一放大装置的非线性特性示于图7-1,求其描述函数。
2图7-2为变放大系数非线性特性,求其描述函数。
7-3求图7-3所示非线性环节的描述函数。
8-4图7-4给出几个非线性特性,分别写出其基准描述函数公式,并在复平面上大致画出其基准描述函数的负倒数特性。
图7-3
图7-4
6-5判断图7-5所示各系统是否稳定?
-丄与KnW(jco)的交点是稳定工作
点还是不稳定工作点?
图7-5
7-6图7-6所示为继电器控制系统的结构图,其线性部分的传递函数为
W(s)=
(54-1)(0.55+1)(0.15+1)
试确定自持振荡的频率和振幅。
7-7图7-7所示为一非线性系统,用描述函数法分析其稳定性。
8-8求下列方程的奇点,并确定奇点类型。
(1)x-(l-x2)x+x=0
(2)x-(0.5-3x2)x+x+x2=0
7-9利用等斜线法lUlj出下列方程的相平面图
(1)x+|i+x=0
(2)X+X4-x=0
7-10系统示于图7-8,设系统原始条件是静止状态,试绘制相轨迹。
其系统
输入为
(1)(t)=A,A>
ee
(2)xr(r)=A+Bt,A>
ee
7-11图7-9为变增益非线性控制系统结构图,其中K=l,k=0.2,e0=l,
并且参数满足如下关系
1十1
2^kKT
试绘制输入量为
(1)£
(f)=A,A>
(2)百⑴=A+Bt,A>
时,以0-£
为坐标的相轨迹。
图7-8
m
9-1求下列函数的z变换。
)=1-严
/'
(/)=coscot
(3)
f(k)=ak
8-
2证明下列关系式。
(2)Zltf(t)]=-Tz^-F⑵
az
8-3求下列函数的z变换。
9-
(1)F(5)=4
(4)F(s)=
$(s+d)
(厂是采样周期)
e-,,T
(5)F(s)=
(s+a)
7-4求下列函数的z反变换。
F⑵=心"
2
(z-l)(z-厂)
F(z)=7
(z-1)2("
2)
F(z)=r
(z+1尸("
IF
2好-1)
(?
+1)2
(T是采样周期)
9-5用z变换方法求解下列差分方程,结果以/(Q表示。
(1)f(k+2)+2/伙+1)+/•⑹》伙)
/(0)=0,/
(1)=0,讥幻=k(k=0,1,2,……)
(2)f(k+2)-4/伙)=cosk7r
/(0)=1J⑴=()(k=0,1,2,……)
(3)于伙+2)+5.f伙+l)+6.f(£
)=cosf;
r(k=0丄2,)
/(0)=0,/
(1)=1
8-6求图P8-1输出环节的z变换(T是采样周期)。
图P8-1
图P8-2
图P8-3
图P8-4
8-7求图P8-2所示系统的开环和闭环脉冲传递函数。
8-8图P8-2所示系统所冇采样开关均为同步釆样开关,求该系统的
E(z)/F(z),X「(z)/X,(z),其中
8-9应用稳定判据,分析习题8-7系统的临界放大系数斤与采样周期T的关系(设QO,7>
0)o
8-10己知一采样系统如图P8-4所示,其中采样周期徉Is,试求扫8时系统稳定性,并求使&
值稳定的&
值范围。
8-11己知图出-5各系统开环脉冲传递函数的零极点分布,试分别绘制根轨迹。
图P8-5
8-12已知一采样系统如图P8-4所示,其中,采样周期徉Is,试绘制叭"
(%)
的对数频率特性,判断系统的稳定性,求相角裕量/KJo8-13数字控制系统结构图如下P8-6所示,设采样周期&
1S,试求
(1)未校正系统闭环极点,并判断稳定性。
图P8-6
(2)XQ"
时,按最少拍设计,求〃(z)表达式,并求X(.(z)的级数展开式。
8-14结构如图P8-7(a)所示的数字控制系统
・%
I町
Xc(nT)
(“+l)7・
(b)
图P8-7
其中t=ciT,d为正整数,T为采样周期。
试设计数字控制器D(z),使系统在单位阶跃输入作用下,输出SXc(nT)满
足图P8-7(b)所示的波形。
5-5用奈氏稳定判据判断下列反馈系统的稳定性,各系统开环传递函数如下
Kg+l)5(T,^+1)(T25+1)