北师大版初中数学七年级下册第二次月考试题陕西师大附中Word文档格式.docx

北师大版初中数学七年级下册第二次月考试题陕西师大附中Word文档格式.docx

《北师大版初中数学七年级下册第二次月考试题陕西师大附中Word文档格式.docx》由会员分享，可在线阅读，更多相关《北师大版初中数学七年级下册第二次月考试题陕西师大附中Word文档格式.docx（24页珍藏版）》请在冰豆网上搜索。

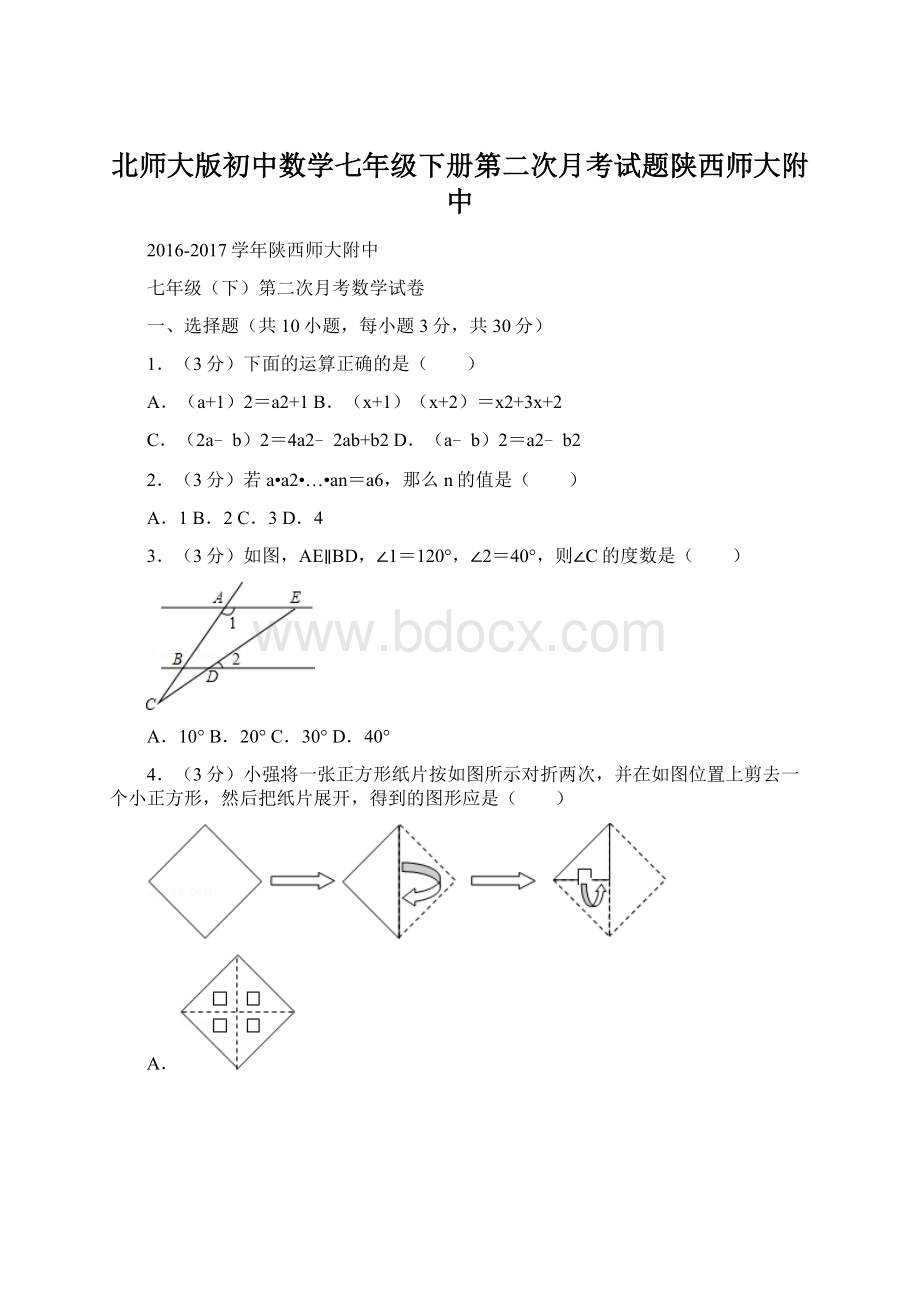
A．36B．54C．63D．72

8．（3分）如图，在△ABC中，∠A＝36°

，AB＝AC，BD是△ABC的角平分线．若在边AB上截取BE＝BC，连接DE，则图中等腰三角形共有（　　）

A．2个B．3个C．4个D．5个

9．（3分）已知△ABC中，AB＝AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是60cm和38cm，则△ABC的腰和底边长分别为（　　）

A．24cm和12cmB．16cm和22cmC．20cm和16cmD．22cm和16cm

10．（3分）如图，已知点P是线段AB上一动点（不与端点A，B重合），△APC和△PBD都是等边三角形，连接AD、BC交于点I，并与PC、PD交于点E、F，则有下列结论：

①AD＝BC；

②等边△PEF；

③∠CID＝120°

；

④∠ECF＝∠EDF，其中正确的有（　　）

A．1个B．2个C．3个D．4个

二、填空题（共8小题，每题3分，共24分）

11．（3分）如果（a+b+1）（a+b﹣1）＝63，那么a+b的值为　　．

12．（3分）某龙舟队参加“国际龙舟节”1000米比赛项目时，路程y（米）与时间x（分钟）之间的图象如图所示，根据图中提供的信息，该龙舟队的比赛成绩　　分钟．

13．（3分）若x

，则

＝　　．

14．（3分）如图，在△ABC中，BC＝6cm，BP、CP分别是∠ABC、∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是　　cm．

15．（3分）如图，D是AB边上的中点，将△ABC沿过点D的直线DE折叠．使点A落在BC边上F处，若∠B＝65°

，则∠BDF＝　　°

．

16．（3分）如图，等腰△ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最小值为　　cm．

17．（3分）已知一个面积为S的等边三角形，现将其各边n（n为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．当n＝k时，共向外作出了　　个小等边三角形，这些小等边三角形的面积和为　　（用含k的式子表示）．

18．（3分）如图，△ABC中，AB＝AC，∠BAC＝54°

，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为　　度．

三、解答题（共46分）

19．（12分）计算题

（1）（2a+5b）（a﹣3b）；

（2）（3x﹣2y）2﹣（3x+2）（2y﹣3x）；

（3）（3a+b﹣2）（3a﹣b+2）；

（4）

20．（8分）若x2+y2＝5，xy＝2．求值：

（1）（x+y）2．

（2）x﹣y．

（3）

21．（6分）尺规作图：

已知∠AOB，试在∠AOB内确定一点P，使点P到OA，OB的距离相等，并且到M，N两点的距离也相等．（不写作法，保留作图痕迹）

22．（8分）如图，△ABC与△ADE均为等边三角形，点D在BC上，连接CE．求证：

BD＝CE．

23．（12分）如图，在△ABC中，D为BC的中点，过D点的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF，并交AB于点E，连接EG，EF．

（1）求证：

BG＝CF．

（2）请你猜想BE+CF与EF的大小关系，并说明理由．

2016-2017学年陕西师大附中七年级（下）第二次月考数学试卷

参考答案与试题解析

【分析】利用完全平方公式化简，即可得到结果．

【解答】解：

A、（a+1）2＝a2+2a+1，错误；

B、（x+1）（x+2）＝x2+3x+2，正确；

C、（2a﹣b）2＝4a2﹣4ab+b2，错误；

D、（a﹣b）2＝a2﹣2ab+b2，错误；

故选：

B．

【点评】此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．

【分析】直接利用同底数幂的乘法运算法则计算得出答案．

∵a•a2•…•an＝a6，

∴1+2+..+n＝6，

解得：

n＝3．

【点评】此题主要考查了同底数幂的乘法运算，正确掌握运算法则是解题关键．

【分析】由AE∥BD，根据两直线平行，同位角相等，即可求得∠CBD的度数，又由对顶角相等，即可得∠CDB的度数，由三角形内角和定理即可求得∠C的度数．

∵AE∥BD，

∴∠CBD＝∠1＝120°

，

∵∠BDC＝∠2＝40°

，∠C+∠CBD+∠CDB＝180°

∴∠C＝20°

【点评】此题考查了平行线的性质与三角形内角和定理．注意两直线平行，同位角相等．

【分析】对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．

严格按照图中的顺序向左对折，向上对折，从直角三角形的一直角边的正中间剪去一个正方形，展开后实际是从正方形的一条对角线上剪去两个小长方形，得到结论．故选B．

【点评】本题主要考查学生的动手能力及空间想象能力．

【分析】根据一次函数的定义可知，x为自变量，y为函数，也叫因变量；

x取全体实数；

y随x的变化而变化；

可以用三种形式来表示函数：

解析法、列表法和图象法．

正确；

而y随x的变化而变化；

错误；

⑤y与x的关系还可以用列表法和图象法表示，正确；

【点评】本题考查了一次函数的定义，是基础知识，比较简单．

【分析】从已知条件结合图形，根据三角形的内角和定理以及等腰三角形的两个底角相等，得它的两个底角是

，再根据直角三角形的两个锐角互余，可得答案．

∵等腰三角形的顶角是n°

∴底角是

∴它的一腰上的高与底边的夹角＝90°

﹣

＝

【点评】此题主要考查了三角形的内角和定理以及等腰三角形的性质；

题目比较简单，思路直接，属于基础题．

【分析】过E作EF⊥BC于F，根据角平分线性质求出EF＝DE＝8，根据三角形面积公式求出即可．

过E作EF⊥BC于F，

∵CD是AB边上的高，BE平分∠ABC，交CD于点E，DE＝8，

∴DE＝EF＝8，

∵BC＝18，

∴

×

BC×

EF＝

18×

8＝72，

D．

【点评】本题考查了角平分线性质的应用，能根据角平分线性质求出EF＝DE＝8是解此题的关键，注意：

在角的内部，角平分线上的点到角的两边的距离相等．

【分析】根据已知条件分别求出图中三角形的内角度数，再根据等腰三角形的判定即可找出图中的等腰三角形．

∵AB＝AC，

∴△ABC是等腰三角形；

∵AB＝AC，∠A＝36°

∴∠ABC＝∠C＝72°

∵BD是△ABC的角平分线，

∴∠ABD＝∠DBC＝

∠ABC＝36°

∴∠A＝∠ABD＝36°

∴BD＝AD，

∴△ABD是等腰三角形；

在△BCD中，∵∠BDC＝180°

﹣∠DBC﹣∠C＝180°

﹣36°

﹣72°

＝72°

∴∠C＝∠BDC＝72°

∴BD＝BC，

∴△BCD是等腰三角形；

∵BE＝BC，

∴BD＝BE，

∴△BDE是等腰三角形；

∴∠BED＝（180°

）÷

2＝72°

∴∠ADE＝∠BED﹣∠A＝72°

＝36°

∴∠A＝∠ADE，

∴DE＝AE，

∴△ADE是等腰三角形；

∴图中的等腰三角形有5个．

【点评】此题考查了等腰三角形的判定，用到的知识点是等腰三角形的判定、三角形内角和定理、三角形外角的性质、三角形的角平分线定义等，解题时要找出所有的等腰三角形，不要遗漏．

【分析】连接BD，根据线段垂直平分线的性质可得到BD＝AD，可知两三角形周长差为AB，结合条件可求得腰长，再由周长可求得BC，可得出答案．

如图，连接BD，

∵D在线段AB的垂直平分线上，

∴BD+DC+BC＝AC+BC＝38cm，

且AB+AC+BC＝60cm，

∴AB＝60cm﹣38cm＝22cm，

∴AC＝22cm，

∴BC＝38cm﹣AC＝38cm﹣22cm＝16cm，

即等腰三角形的腰为22cm，底为16cm，

【点评】本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．

【分析】根据SAS定理得出△APD≌△CPB，由全等三角形的性质即可得出AD＝BC，故①正确；

由平角的定义可得出∠EPF＝60°

，再根据SAS定理可得出△APE≌△CPF，故可得出PE＝PF，即△PEF是等边三角形，故②正确；

由①可知∠PAD＝∠PCB，故∠CAE+∠ACP＝∠CAP+∠ACP＝120°

，因为∠CID是△ACI的外角，故∠CID＝∠CAE+∠ACP＝120°

，故③正确；

由于AP≠PD，所以∠PAE≠∠EDF，由①知，∠PAD＝∠ECF，故∠ECF≠∠EDF，故④错误．

∵△APC和△PBD都是等边三角形，

∴AP＝PC，PD＝PB，∠APC＝∠BPD＝60°

∴∠APD＝∠BPC＝120°

在△APD与△CPB中，

∴△APD≌△CPB（SAS），

∴AD＝BC，故①正确；

∵∠APC＝∠BPD＝60°

∴∠EPF＝60°

∵△APD≌△CPB，

∴∠PAE＝∠PCF，

在△APE与△CPF中，

∴△APE≌△CPF（ASA），

∴PE＝PF，即△PEF是等边三角形，故②正确；

∵由①可知∠PAD＝∠PCB，

∴∠CAE+∠ACP＝∠CAP+∠ACP＝120°

∵∠CID是△ACI的外角，

∴∠CID＝∠CAE+∠ACP＝120°

∵AP≠PD，

∴∠PAE≠∠EDF，由①知，∠PAD＝∠ECF，

∴∠ECF≠∠EDF，故④错误．

【点评】本题考查的是全等三角形的判定与性质，熟知SAS，ASA，SSS，HL等判定定理是解答此题的关键．

11．（3分）如果（a+b+1）（a+b﹣1）＝63，那么a+b的值为　±

8　．

【分析】将a+b看做整体，用平方差公式解答，求出a+b的值即可；

∵（a+b+1）（a+b﹣1）＝63，

∴（a+b）2﹣12＝63，

∴（a+b）2＝64，

a+b＝±

8；

故答案为：

±

8

【点评】本题考查了平方差公式，整体思想的利用是解题的关键，需要同学们细心解答，把（a+b）看作一个整体．

12．（3分）某龙舟队参加“国际龙舟节”1000米比赛项目时，路程y（米）与时间x（分钟）之间的图象如图所示，根据图中提供的信息，该龙舟队的比赛成绩　4.8　分钟．

【分析】比赛成绩是当y＝1000时对应的x的值，所以须求后段的直线解析式．

设后段的解析式为y＝kx+b，由图象过（4，800）和（4.5，925），

得

解之得

所以解析式为y＝250x﹣200，

当y＝1000时250x﹣200＝1000，解之得x＝4.8．

所以该龙舟队的比赛成绩是4.8分钟．

故答案是：

4.8．

【点评】考查了函数的图象．分段函数必须搞清楚各段表示的意义及所求问题对应的部分．

＝　

　．

【分析】已知等式两边平方后，整理求出x2+

的值，所求式子分子分母除以x2变形后，将x2+

的值代入计算即可求出值．

已知等式平方得：

（x﹣

）2＝x2﹣2+

＝16，即x2+

＝18，

则

【点评】此题考查了分式的化简求值，熟练掌握完全平方公式是解本题的关键．

14．（3分）如图，在△ABC中，BC＝6cm，BP、CP分别是∠ABC、∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是　6　cm．

【分析】分别利用角平分线的性质和平行线的判定，求得△DBP和△ECP为等腰三角形，由等腰三角形的性质得BD＝PD，CE＝PE，那么△PDE的周长就转化为BC边的长，即为6cm．

∵BP、CP分别是∠ABC和∠ACB的角平分线，

∴∠ABP＝∠PBD，∠ACP＝∠PCE，

∵PD∥AB，PE∥AC，

∴∠ABP＝∠BPD，∠ACP＝∠CPE，

∴∠PBD＝∠BPD，∠PCE＝∠CPE，

∴BD＝PD，CE＝PE，

∴△PDE的周长＝PD+DE+PE＝BD+DE+EC＝BC＝6cm．

【点评】此题主要考查了平行线的判定，角平分线的性质及等腰三角形的性质等知识点．本题的关键是将△PDE的周长就转化为BC边的长．

，则∠BDF＝　50　°

【分析】先根据图形翻折不变性的性质可得AD＝DF，根据等边对等角的性质可得∠B＝∠BFD，再根据三角形的内角和定理列式计算即可求解．

∵△DEF是△DEA沿直线DE翻折变换而来，

∴AD＝DF，

∵D是AB边的中点，

∴AD＝BD，

∴BD＝DF，

∴∠B＝∠BFD，

∵∠B＝65°

∴∠BDF＝180°

﹣∠B﹣∠BFD＝180°

﹣65°

＝50°

50．

【点评】本题考查的是图形翻折变换的图形能够重合的性质，以及等边对等角的性质，熟知折叠的性质是解答此题的关键．

16．（3分）如图，等腰△ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最小值为　8　cm．

【分析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．

连接AD，

∵△ABC是等腰三角形，点D是BC边的中点，

∴AD⊥BC，

∴S△ABC＝

BC•AD＝

4×

AD＝12，解得AD＝6cm，

∵EF是线段AB的垂直平分线，

∴点B关于直线EF的对称点为点A，

∴AD的长为BM+MD的最小值，

∴△BDM的周长最短＝（BM+MD）+BD＝AD+

BC＝6+

4＝6+2＝8cm．

8．

【点评】本题考查的是轴对称﹣最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．

17．（3分）已知一个面积为S的等边三角形，现将其各边n（n为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．当n＝k时，共向外作出了　3（k﹣2）　个小等边三角形，这些小等边三角形的面积和为　

S　（用含k的式子表示）．

【分析】根据前三个图形小等边三角形的个数，推出n＝8时共向外作出了18个等边三角形，归纳总结出第k个图形即n＝k时，共向外作出的小等边三角形的个数，然后利用相似三角形的面积之比等于相似比的平方求出一个小等边三角形的面积，根据归纳出的个数即可求出所有小等边三角形的面积之和．

由第1个图形可知：

n＝3时，共向外作出了3（3﹣2）个三角形；

由第2个图形可知：

n＝4时，共向外作出了3（4﹣2）个三角形；

…

所以当n＝8时，共向外作出了3（8﹣2）＝18个三角形；

当n＝k时，共向外作出了3（k﹣2）个三角形；

又第k个图形中的每一个小三角形都与最大的等边三角形相似，相似比为1：

k，

所以面积比为1：

k2，且最大的等边三角形的面积为S，

则一个小等边三角形的面积为

S，

所以这些小等边三角形的面积和是

S．

3（k﹣2）；

【点评】此题考查学生会根据题意归纳总结出一般性的结论，掌握相似三角形的判断及性质，是一道综合题．

，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为　108　度．

【分析】连接OB、OC，根据角平分线的定义求出∠BAO，根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA＝OB，根据等边对等角可得∠ABO＝∠BAO，再求出∠OBC，根据全等三角形的性质可得OB＝OC，根据等边对等角求出∠OCB＝∠OBC，根据翻折的性质可得OE＝CE，然后根据等边对等角求出∠COE，再利用三角形的内角和定理列式计算即可得解．

如图，连接OB、OC，

∵∠BAC＝54°

，AO为∠BAC的平分线，

∴∠BAO＝

∠BAC＝

54°

＝27°

又∵AB＝AC，

∴∠ABC＝

（180°

﹣∠BAC）＝

﹣54°

）＝63°

∵DO是AB的垂直平分线，

∴OA＝OB，

∴∠ABO＝∠BAO＝27°

∴∠OBC＝∠ABC﹣∠ABO＝63°

﹣27°

∵AO为∠BAC的平分线，AB＝AC，

∴△AOB≌△AOC（SAS），

∴OB＝OC，

∴∠OCB＝∠OBC＝36°

∵将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，

∴OE＝CE，

∴∠COE＝∠OCB＝36°

在△OCE中，∠OEC＝180°

﹣∠COE﹣∠OCB＝180°

＝108°

108．

【点评】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，以及翻折变换的性质，综合性较强，难度较大，作辅助线，构造出等腰三角形是解题的关键．

【分析】

（1）原式利用多项式乘以多项式法则计算即可求出值；

（2）原式利用完全平方公式，以及多项式乘以多项式法则计算即可求出值；

（3）原式利用平方差公式，以及完全平方公式计算即可求出值；

（4）原式利用多项式除以单项式法则计算即可求出值．

（1）原式＝2a2﹣ab﹣15b2；

（2）原式＝9x2﹣12xy+4y2﹣6xy+9x2﹣4y+6x＝18x2﹣18xy+4y2﹣4y+6x；

（3）原式＝9a2﹣（b﹣2）2＝9a2﹣b2+4b﹣4；

（4）原式＝﹣0.5+ab+

a2b2．

【点评】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．

【分析】根据完全平方公式即可求出答案．

（1）（x+y）2＝x2+y2+2xy＝5+4＝9

（2）（x﹣y）2＝（x+y）2﹣4xy＝9﹣8＝1

∴x﹣y＝±

1

（3）原式＝

当x﹣y＝1时，

∴原式＝﹣

＝﹣

当x﹣y＝﹣1时，

∴原式＝

【点评】本题考查完全平方公式，解题的关键是熟练运用完全平方公式，本题属于基础题型．

【分析】作∠AOB的平分线OC，作线段MN的垂直平分线EF，射线OC交EF于点P，点P即为所求．

如图点P即为所求．

【点评