高二数学上册 94《三阶行列式》教案3 沪教版文档格式.docx

高二数学上册 94《三阶行列式》教案3 沪教版文档格式.docx

《高二数学上册 94《三阶行列式》教案3 沪教版文档格式.docx》由会员分享，可在线阅读，更多相关《高二数学上册 94《三阶行列式》教案3 沪教版文档格式.docx（12页珍藏版）》请在冰豆网上搜索。

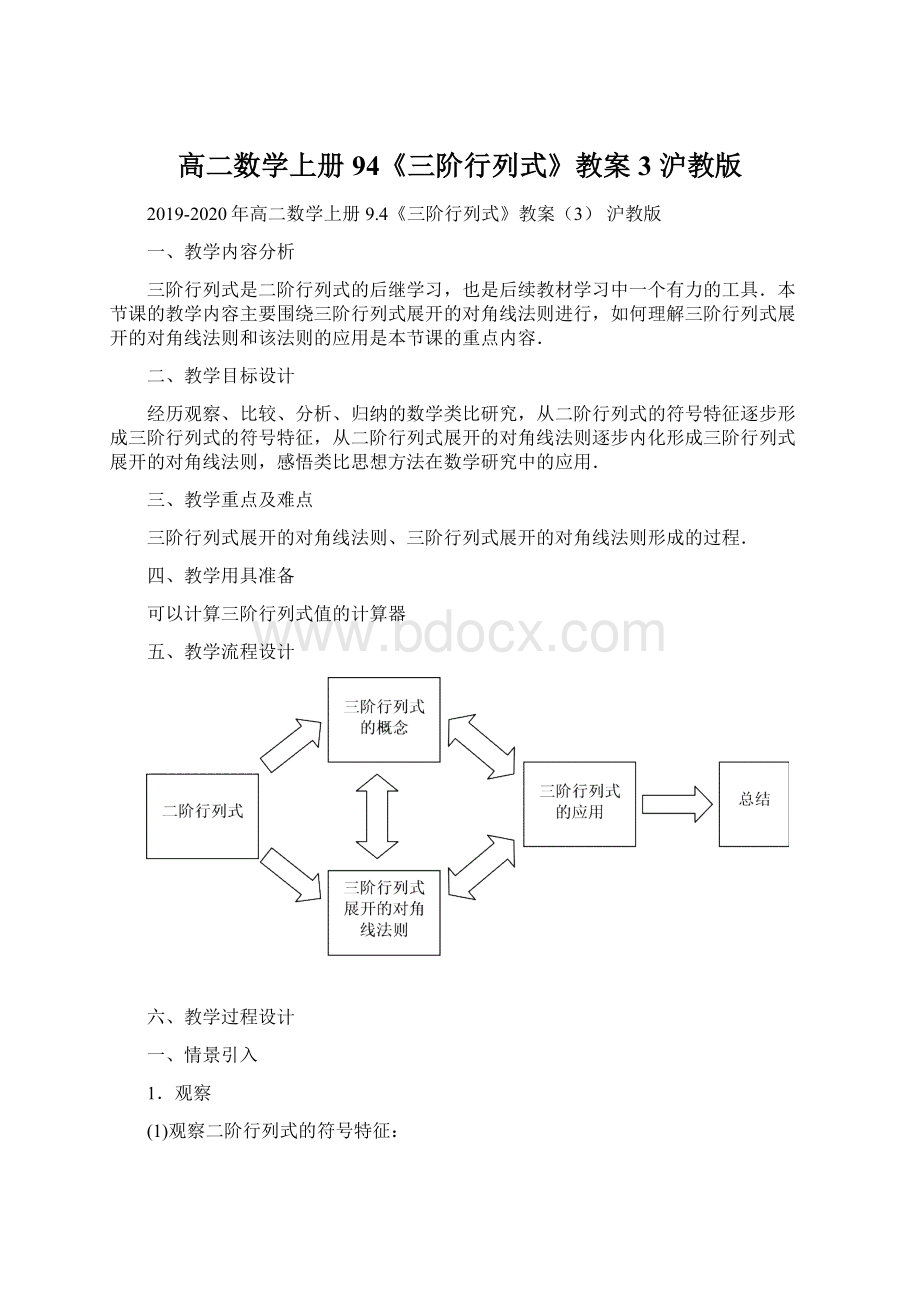
（1）二阶行列式算式的符号有哪些特征？

（2）你能总结一下二阶行列式的展开式有哪些特征吗？

[说明]

（1）请学生观察二阶行列式的符号特征，主要是观察二阶行列式有几个元素，这几个元素怎么分布？

从而可以类比得到三阶行列式的符号特征．

（2）请学生观察和总结二阶行列式的展开式特征，可以提示学生主要着力于以下几个方面：

①观察二阶行列式的展开式有几项？

②二阶行列式的展开式中每一项有几个元素相乘；

这几个元素在行列式中的位置有什么要求吗？

③二阶行列式的元素在其展开式中出现了几次？

每个元素出现的次数一样吗？

二、学习新课

1．新课解析

【问题探讨】

结合情景引入的两个思考问题，教师可以设计一些更加细化的问题引导学生发现二阶行列式的符号特征以及二阶行列式的展开式特征，从而类比得到三阶行列式相应特征．比如教师可以设计如下几个问题：

问题一，通过学习和观察，我们发现二阶行列式就是表示四个数（或式）的特定算式，这四个数分布成两行两列的方阵，那么三阶行列式符号应该有怎么样的特征呢？

问题二，说出二阶行列式的展开式有哪些特征？

（①二阶行列式的展开式共有两项；

②二阶行列式的展开式中每一项有两个元素相乘；

③相乘的两个元素在行列式位于不同行不同列；

④二阶行列式的元素在其展开式中出现了一次，而且每个元素出现的次数是一样的．）

问题三，二阶行列式展开式就是：

主对角线的元素乘积减去副对角线的元素的乘积．我们可以根据二阶行列式展开式的特征类比研究三阶行列式

按对角线展开后展开式应该具有的特征．那么三阶行列式的展开式中每一项有几个元素相乘？

对这些可以相乘的元素有什么要求？

（3个．这3个可以相乘的元素应该位于不同行不同列．）

问题四，三阶行列式的展开式的项中有哪些元素的乘积？

二阶行列式的元素在其展开式中出现了一次，而且每个元素出现的次数是一样的．那么，请你猜测一下在三阶行列式的展开式中，每个元素应该出现几次呢？

你猜测的依据是什么？

二阶行列式与三阶行列式有必然的内在联系，上述各个问题的探讨可以帮助学生学习三阶行列式的概念，并能意识到三阶行列式的展开式中必然会出现，，，，，．至于展开式中各项符号的确定，可以组织学生通过以下实验尝试解决．

【实验探究】

【工作1】

请你对，，，，，，，，分别赋值：

______，______，______，______，______，______，______，______，______，

利用计算器，计算得：

____________．

【工作2】

填写下表：

号

符

项

积

乘

各

序

=

_____

各项之和

猜想1

猜想2

猜想3

…

【工作3】

由上述计算结果，可以发现三阶行列式按对角线展开后展开式应该是：

____________________________________．

[说明]

（1）以上实验主要由学生合作完成，实验的目的主要是让学生经历猜想预测、实验检验、获得新知的过程；

（2）为了便于研究，教师应该提示学生在完成工作

（1）时，，，，，，，，，应该分别赋不同的值，而且不要赋为0；

（3）教师可以将学生分成数个学习小组，合作实验研究，并交流研究结果，最后由教师总结；

（4）通过上述研究，可以引导学生发现：

；

（5）三元一次方程组

经消元后，得：

因而发现是符合引入该记号的实际意义的。

但这个展开式比较复杂，教师可以组织学生讨论：

你觉得怎样记忆这个展开式最好？

并逐渐引导学生发现如下记忆方法：

如图，用红线连接的三个元素的乘积取“﹢”，用黑线连接的三个元素的乘积取“﹣”，而这六个结果的代数和就是三阶行列式

的展开式．这种展开方法叫做三阶行列式展开的对角线法则．

2．例题解析

例题1.用对角线法则展开行列式：

（1）

（2）

（3）

例题2.把下面的算式写成一个三阶行列式：

（1）

（2）

解：

本例题主要是考查学生的逆向思维能力，同时为例题3做好准备工作．对照三阶行列式的展开式，学生可以写出正确结论，但要注意这是两个开放性问题，答案并不唯一．

例题3.如图,在平面直角坐标系中,点、、的坐标分别为、、，求的面积．

（1）本例题的答案不唯一，除了上述的结果之外，还可以是

，

等等；

（2）由的面积

可知，、、三点共线的充分必要条件为

（3）仔细分析，不难发现

并不能当公式应用，原因是行列式

的值可能为负数．事实上，当位于线段下方时，该行列式的值就是负数．的面积公式应该是：

3．问题拓展

比较例题1的三个行列式，你可以得到些什么样的结论？

你能证明这些结论吗？

〖参考〗

（1）将一个三阶行列式的行（列）变为列（行）所得到的新三阶行列式与原行列式相等；

（2）交换一个三阶行列式的两行（或列），行列式改变符号．

设计这样一个问题基于两方面考虑：

一，本问题的解答有助于学生理解为什么例题2和例题3的答案不唯一；

二，新课程标准要求教师“尊重学生现有的认知水平和差异”，不同的学生对数学的需要也不同．因此，我们教师的教学内容不仅要满足学生对知识的基础性需求，而且还有满足学生对知识的发展性需求．

三、巩固练习

教材第96页，练习9.4

（1）．

四、课堂小结

1、三阶行列式的概念；

2、三阶行列式展开的对角线法则．

五、作业布置

根据学生的具体情况，对习题册中的问题进行增减．

七、教学设计说明

本节课的教学内容是三阶行列式的概念和三阶行列式展开的对角线法则．从内容上看，这部分知识概念性特别强，如果仅仅按照课本内容讲授，容易让学生感到数学的枯燥乏味，对培养学生的学习兴趣是无益的，学生也很难感受到数学的魅力所在．新课程标准提倡，过程比结果重要，能力比知识重要．考虑到学生已经学习过二阶行列式的概念和二阶行列式展开的对角线法则，我把本节课的教学模式设计为从学生现有的实际知识水平和能力水平出发，通过深究二阶行列式的特征，类比研究三阶行列式，让学生体会类比思想方法在数学研究中的作用，感悟数学的无穷魅力．诚然，三阶行列式展开的对角线法则比二阶行列式展开的对角线法则要复杂的多，但两者之间并不是毫无联系，所以本节课的教学应该着力研究二阶行列式展开的对角线法则的特征，并引导学生将这种特征逐渐迁移到三阶行列式展开的对角线法则中．

2019-2020年高二数学上册第八章平面向量的坐标表示（章综合）课件沪教版

一、选择题

1．已知,则是三点构成三角形的　　　（　　）

A.充分不必要条件B.必要不充分条件

C.充要条件D.既不充分也不必要条件

2．已知向量，且，则的坐标是（）

A.B.C.D.

3．，则与的夹角是（　　）

A.　B.　C.　D.

4．在平行四边形中，若，则必有（）

A.B.C.是矩形D.是正方形

5．已知

，与的夹角为，则等于（）

A.1　　　　B.　２　　　　　C.　　D.－1

6．已知下列各式：

（1）；

（2）；

（3）；

（4），其中正确的有（）

A.　1个B.2个　C.3个　D.4个

7．若

（）

A.B.C.D.

8．已知，则的取值范围是（）

A.[3，8]B.（3，8）C.[3，13]D.（3，13）

9．已知，则等于（）

A.23B.35C.D.

10．设

，则C、D的坐标分别是（）

11．已知向量且,则=（）.

A．B.C.D.

12．已知向量

A．30°

B．60°

C．120°

D．150°

13．若，且，则向量与的夹角为（）

A.30°

B.60°

C.120°

D.150°

14．若三点共线，则（）

A.B.3C.D.51

15．已知、均为单位向量，它们的夹角为60°

，那么=（）.

A．B．C．D．4

16．已知分别是的边上的中线,且,则为（）

A.B.C.D.

二、填空题

17．若的方向相反，且

18．化简：

（1）_____________。

（2）______________。

（3）______________。

19．已知向量

，且A、B、C三点共线，则k=

20．分别是的边的中点，且给出下列命题

①②③④

其中正确的序号是_________。

21．已知不共线，，当______时，共线。

22．若向量与垂直，与垂直，则非零向量与的夹角是______..

23．已知平面上三点A、B、C满足则的值等于.

24．已知如果与的夹角是钝角，则的取值范围是________________。

三、解答题

25．如图，是以向量为边的平行四边形，又，试用表示。

26．已知向量

求的值.

27．已知平面向量

（1）证明：

（2）若存在不同时为零的实数和，使

，且，试求函数关系式；

28．已知向量

.

求函数f（x）的最大值，最小正周期，并写出f（x）在[0，π]上的单调区间.

参考解答

1－5BABCA6－10BBCCA11－15ACCBC16B

17.18.

（1）　

（2）　　（3）19.k=20.①②③④

21.22.23.－2524.或且

25．，，　　

26．解法一：

由已知，得

又

所以

解法二：

由已知，得

27．

（1）易证，从略　　

（2）

28．解：

=.