六年级上册数学第四单元《比》的教案MicrosoftWord文档Word文档格式.docx
《六年级上册数学第四单元《比》的教案MicrosoftWord文档Word文档格式.docx》由会员分享,可在线阅读,更多相关《六年级上册数学第四单元《比》的教案MicrosoftWord文档Word文档格式.docx(16页珍藏版)》请在冰豆网上搜索。
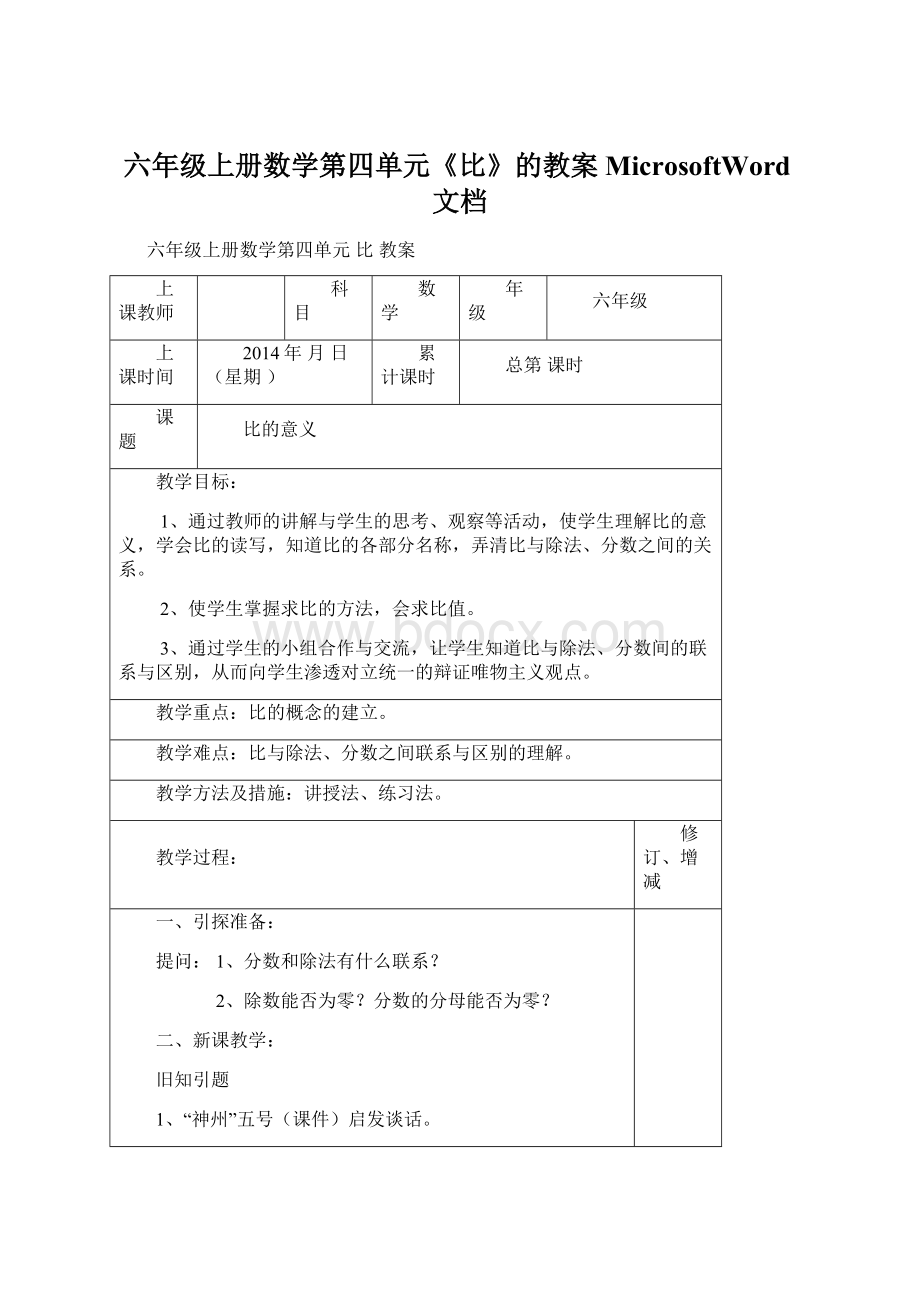
————15—10=5(厘米)
②长是宽的几倍?
————15÷
10=
————长是宽的倍
③宽是长的几分之几?
————10÷
15=————宽是长的倍
在日常生活和和工农业生产中,常常需要对两个数量进行比较.比较的方法我们已经学过两种(比较两个数量之间相差关系用减法;
比较两个数量之间的倍数关系用除法),
师:
在这里呢,老师要告诉大家:
②和③式,我们还可以改写成一种新的表达形式。
我们把它称为比。
(师板书课题:
比)
你们看到老师在黑板上写“比”这个字的时候,你们想到了什么?
谁愿意来说说?
生1:
什么是比?
生2:
比怎么读写?
为什么要学比?
生3:
比有什么用?
大家一下子提了这么多的问题,那我们先来学习什么是比。
探索新知,解决问题。
(1)
观察国旗长与宽的比。
无论是长除以宽,还是宽除以长,都表示长和宽之间的倍数关系,这是也可以把两个数量间的关系说成是两个数量的比。
如(长是宽的几倍也可以说成长和宽的比是15比10)
宽是长的几分之几?
可以怎么说?
现在有没有同学愿意试着说一说?
宽和长的比是10比15。
很好。
比是除法的另一种表达形式,它也表示两个数量之间的倍关系,只是形式不同。
(2)思考路程与时间的比。
下面请大家在看一道题目:
神州五号进入运行轨道后,在距地350千米的高空作圆周运动,平均90分钟绕地球一周,大约运行42252千米。
我们已知(路程)和(时间),它们之间有什么关系呢?
路程÷
时间=速度
42252÷
90=(千米)
下面请你们思考一下:
我们能不能用比来表示路程与时间的关系?
同桌之间讨论一下。
请一位同学来说说。
路程除以时间可以说成是路程与时间的比是42252:
90
(3)联系区别。
大家观察我们的两个例子,你们有什么发现吗?
第一题中,长和宽的单位都是长度单位,
第二题中,路程和时间的单位是不同的。
对,我们把例1中的这两个量称为同类量,把例2中的两个量称为不同类量。
同类量和不同类量之间的倍数关系,我们都可以用比来表示。
(4)归纳比的意义。
通过这么的例子,大家现在再用自己的话来说说什么是比?
(引导学生观察前面例子中除法算式和比的对照。
)
只要是两个数相除,都可以写成比的形式。
大家说得已经很接近了,实际上,两个数相除又叫做两个数的比。
根据比的意义,结合身边的事,你能说出一组比吗?
(5)教学比的各部分名称。
说法变了写法、读法以及各部分的名称也就变了。
现在请大家先自学书本P44内容。
现在请一个同学来当当小老师,教大家比的各部分名称。
15
:
10
=
÷
10=
前
比
后
比
项
号
值
大家觉得这个小老师怎样?
你们都记住了吗?
还有什么问题要问她吗?
生问:
什么叫做比值?
如何求比值?
生答:
比的前项除以后项的值就叫做比值。
好,大家都没有问题了吧?
那现在老师要考考你们了!
(出示题目)
3:
0=
15 :
3= 0.5 :
2=
除法,因为比是除法的另一种形式。
说得真好,比实际上就是两个数相除的形式。
因而比与除法有密切联系。
师引导生发现比的各部分和除法算式各部分之间关系。
(四人一组讨论完成下表)
1、比与除法、分数有那些联系
2、比与除法、分数又有什么不同?
联
系(相
当
于)区
别
除法被除数÷
(除号)除数商一种运算
分数分子-(分数线)分母分数值一种数
比前项:
(比号)后项比值一种关系
有的时候,比也会写成分数形式,但实际上它还是一个比,如,应读作15比10。
三、课堂练习,巩固新知
书本P49“做一做”。
四、课堂小结
今天这堂课,学习之后,你们有什么收获呢?
五、布置作业
教科书练习十一第1——3题。
板书设计
比的意义
两个数相除又叫两数的比。
15
10
:
15=10÷
15=
42252:
90=42252÷
90=
前项比号后项比值
教学反思:
比的基本性质
1、能联系商不变的规律和分数的基本性质,理解比的基本性质,并能应用比的基本性质化简比。
2、培养类比、推理、概括等思维能力,渗透数学思想方法。
3、引导学生揭示知识间的联系,向学生进行对立统一的辩证唯物主义教育。
理解比的基本性质,推导化简比的方法,正确化简比。
比值和化简比的区别。
创设情境,引导探究,知识迁移,推理归纳。
一、复习导入
1、比与分数、除法的关系。
老师:
我们已经学习了比的意义,知道比和分数、除法之间有着密切的关系,哪位同学愿意说说比和分数、除法之间有什么联系?
如果学生有困难,可以先完成下表。
填表后再说一说比与分数、除法有怎样的关系。
(多媒体课件展示)
比分数除法
3:
5
3÷
8
2、复习分数的基本性质和商不变的性质。
请大家回忆一下,分数有什么性质?
除法又有什么性质?
它们的内容分别是什么?
(指名回答)
二、新课讲授
1、猜想。
比和分数、除法的关系相当密切,那么,在比中有没有类似的性质呢?
如果有,请同学们猜想一下,可能会是怎样的?
汇报时,让学生说说猜想的根据,老师也可引导学生在“分数的基本性质”上进行替换。
引导学生用语言表述,比的前项相当于分数的分子,后项相当于分母,分数的分子和分母同时乘或除以同一个数(0除外),分数的大小不变。
因此,比的前项和后项同时乘或除以同一个数(0除外),比值不变。
或者比的前项相当于除法中的被除数,后项相当于除数,被除数和除数同时乘或除以同一个数(0除外),商不变。
2、验证。
以小组为单位,讨论、验证一下刚才的猜想是否正确。
学生汇报。
3、小结。
经过同学们的验证,我们知道这个猜想是正确的,并且经过补充使它更完整了,在比中确实存在这种性质。
板书课题:
比的基本性质。
4、化简比。
应用比的基本性质,我们可以把比化成最简单的整数比。
多媒体课件出示例1的第
(1)题。
(1)“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm,(前面展示过),另一面长180cm,宽120cm。
这两面联合国旗长和宽的最简单的整数比分别是多少?
让学生在练习本上写出一小一大两面联合国旗长和宽的比,15:
10和180:
120
你怎样理解最简单的整数比这个概念?
学生讨论,指名回答,达成共识,最简单的整数比必须是一个比,它的前项和后项都是整数,而且前项和后项应该是互质数。
让学生自己尝试把这两个比化成最简单的整数比,然后集体订正答案。
15:
10=(15÷
5):
(10÷
5)=3:
2
180:
120=(180÷
60):
(120÷
60)=3:
提醒学生注意两个比化简的结果,并让学生说说结果相同,说明了什么?
(说明两面国旗大小不同,形状相同。
渗透《国旗法》规定:
旗面应为长方形,其长与高为3与2之比。
联合国统一规定2:
3
联合国为公平处理会员国起见,不论各国如何规定其国旗的纵横比例,于联合国会场或相关国际性的场合,各会员国一律须使用2:
3的国旗,以期达到公平一致。
出示例1的第
(2)题。
(2)把下面各比化成最简单的整数比。
:
0.75:
让学生独立试做,教师巡视指导,请两名学生在黑板上板演。
师生共同讲评。
=(
×
18):
(
18)=3:
4
为什么要乘18?
可能会有学生想到不同方法,教师应给予肯定。
0.75:
2=(0.75×
100):
(2×
100)=75:
200=3:
或(0.75×
4):
4)=3:
老师强调:
不管选择哪种方法,最后的结果都应该是一个最简单的整数比,而不是一个数。
5、反馈练习。
(1)完成教材第46页的“做一做”,集体订正。
在校对、交流的基础上,引导学生对化简比的方法进行小结。
(2)完成教材第48页练习十一的第4—6题。
三、当堂测试
1、把下面各比化成最简单的整数比。
24:
2851:
17
1:
1.2
3:
0.4:
0.52:
0.2
2、改错。
(1)0.48:
0.6化简后是0.8。
(2)21:
12化简后是21:
12。
(3)1:
0.4化简后是
。
3、有一个两位数,十位上的数和个位上的数的比是2:
3。
十位上的数加上2,就和个位上的数相等。
这个两位数是多少?
学完这节课,我们知道了比的基本性质:
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
我们还能够根据比的基本性质,熟练地把比化成最简单的整数比。
希望同学们课后多加练习,灵活运用所学的知识解决一些实际问题。
五、课后作业
1、化简下面各比.
16∶20
2∶
4.5∶6
5∶0.35
2、鞋厂生产的皮鞋,十月份生产双数与九月份生产双数的比是5∶4.十月份生产了2000双,九月份生产了多少双?
板书设计:
比的基本性质
比的基本性质:
比的前项和后项同时乘或除以相同的数(0除外),比值不变
比的基本性质的用途:
化简比
比的应用
1、结合生活实例,使学生进一步掌握按比例分配应用题的结构特点和解题思路,能运用这个知识来解决一些日常工作、生活中的实际问题。
2、培养学生运用知识进行分析、推理等思维能力,以及探求解决问题途径的能力。
3、渗透数学的对应思想及函数思想,培养学生认真审题、独立思考、自觉检验的好习惯,增强学好数学的信心。
进一步掌握按比例分配应用题的结构特点和解题思路。
正确分析解答比例分配应用题
教法:
创设情境,引导探究。
学法:
知识迁移,推理归纳
一、课前组织复习旧知
1、同学们,通过前几节课的学习,我们已经认识了什么是“比”,那么,如果我现在告诉你“数学兴趣小组男生和女生的人数比是5:
4,从这组比中,你能推断出什么信息呢?
”(课件出示题目)
2、追问:
你还可以从中推断出这个兴趣小组的男生和女生可能各有多少人吗?
3、在工农业生产和日常生活中,常常需要把一个数量按照一定的比来分配。
这种分配的方法通常叫做按比例分配。
二、创设情境,导入新知
1、出示书本例2:
2、引导学生弄清题意后,问:
题目中要分配什么?
是按什么进行分配的?
(分配500ml的稀释液;
浓缩液和水的体积按1:
4进行分配。
3、问:
“浓缩液和水的体积1:
4”,是什么意思?
(就是说在500ml的稀释液,浓缩液占1份,水的体积占4份,一共是5份,浓缩液占稀释液的,水的体积占稀释液的。
4、你能求出两种各多少ml吗?
怎样求?
(引导学生进行解题)
①稀释液平均分成的份数:
1+4=5
②学生自主学习、小组内互助,继续解答。
5、展示学生做题方法:
方法一:
①总份数:
4+1=5
②每份是:
500÷
5=100(ml)
③浓缩液有:
100×
1=100(ml)
④水有:
4=400(ml)
答:
浓缩液有100ml,水有400ml。
方法二:
②浓缩液有:
500×
=100(ml)
③水有:
=400(ml)
6、如何检验解答是否正确呢?
(检验的方法有两种:
一是把求得的浓缩液和水的体积相加,看是不是等于稀释液的总体积;
二是把求得的浓缩液和水的体积写成比的形式,看化简后是不是等于1:
4。
7、归纳按比例分配的做题思路:
(1)①根据比先求出总份数。
②求出每份是多少。
③求出各部分的量。
④答题并检验。
(2)①根据比先求出总份数。
②求出各部分数占总数的几分之几。
③运用分数乘法列式计算,求出各部分的量。
三、课题练习:
教科书练习十二第2、3题。
四、巩固提高:
1、有一块试验田,周长200米,长与宽的比是3∶2。
这块试验田的长和宽分别是多少?
2、书P56第11题:
用120cm的铁丝做一个长方体的框架。
长、宽、高的比是3:
2:
1.这个长方体的长、宽、高分别是多少?
五、小结:
说一说在这节课中,你有什么收获?
还有疑惑吗?
六、布置作业:
练习十二第1、4题。
解决“按比分配应用题”
③求出各部分的量。
③运用分数乘法列式计算,求出各部分的量。
④答题并检验
比的应用的练习
1、通过复习使学生更好地掌握除法的意义和计算法则,掌握比的意义和比的基本性质,会熟练地求比值和化简比。
2、通过复习使学生更好地掌握分数应用题的数量关系和解题方法,会熟练地解答分数应用题和按比例分配应用题。
3、进一步提高学生解答应用题的能力。
进一步掌握暗比例分配应用题的结构特点和结题思路。
运用所学概念,灵活解决问。
通过多次练习,让学生小组合作,解决问题。
一、复习比的意义和基本性质
1、比的意义
(1)什么叫做比?
(两个数相除又叫做两个数的比)什么叫做比值?
(比的前项除以后项所得的商.)
(2)以“3∶2”为例,让学生分别说出“比号”“前项”和“后项”。
3∶2=1.5
┇┇┇ ┇
前比后 比
项号项值
(3)比和比值有什么区别和联系呢?
(比值是一个数,是比的前项除以比的后项所得的商,它通常用分数表示,也可以用小数表示,有时还是整数。
而比所表示的是两个数的关系,如3∶2,虽然也可以写成分数的形式
,但仍读作3比2。
特别强调比的后项不能为0)
(4)比和除法、分数的联系
(除号)除数商
分数分子-(分数线)分母分数值
比前项:
(比号)后项比值
2、比的基本性质
(1)复习概念及化简方法
①比的基本性质是什么?
②应用比的基本性质,怎样对整数比进行化简?
③不是整数的比应该怎样化简?
二、合作探究。
学校把栽280棵树的任务,按照六年级三个班的人数分配给各班。
一班有47人,二班有45人,三班有48人。
三个班各应栽树多少棵?
(2)引导学生弄清题意后,问:
题中要把280棵树按照什么进行分配?
(3)根据一班、二班、三班的人数怎样算出各班栽的棵数占总棵数的几分之几?
(4)怎样分别算出各班应种的棵数?
引导学生解答:
1三个班的总人数:
47+45+48=140(人)
2一班应栽的棵数:
(人)
3二班应栽的棵数:
4三班应栽的棵数:
一班栽树94棵,二班栽树90棵,三班栽树96棵。
三、巩固练习。
教科书练习十二第7、8、10题。
四、小结:
今天我们学习了什么知识?
五、作业布置:
教科书练习十二第6、9题。
比的应用的练习