二次函数难题练习及答案一.doc

二次函数难题练习及答案一.doc

《二次函数难题练习及答案一.doc》由会员分享，可在线阅读，更多相关《二次函数难题练习及答案一.doc（10页珍藏版）》请在冰豆网上搜索。

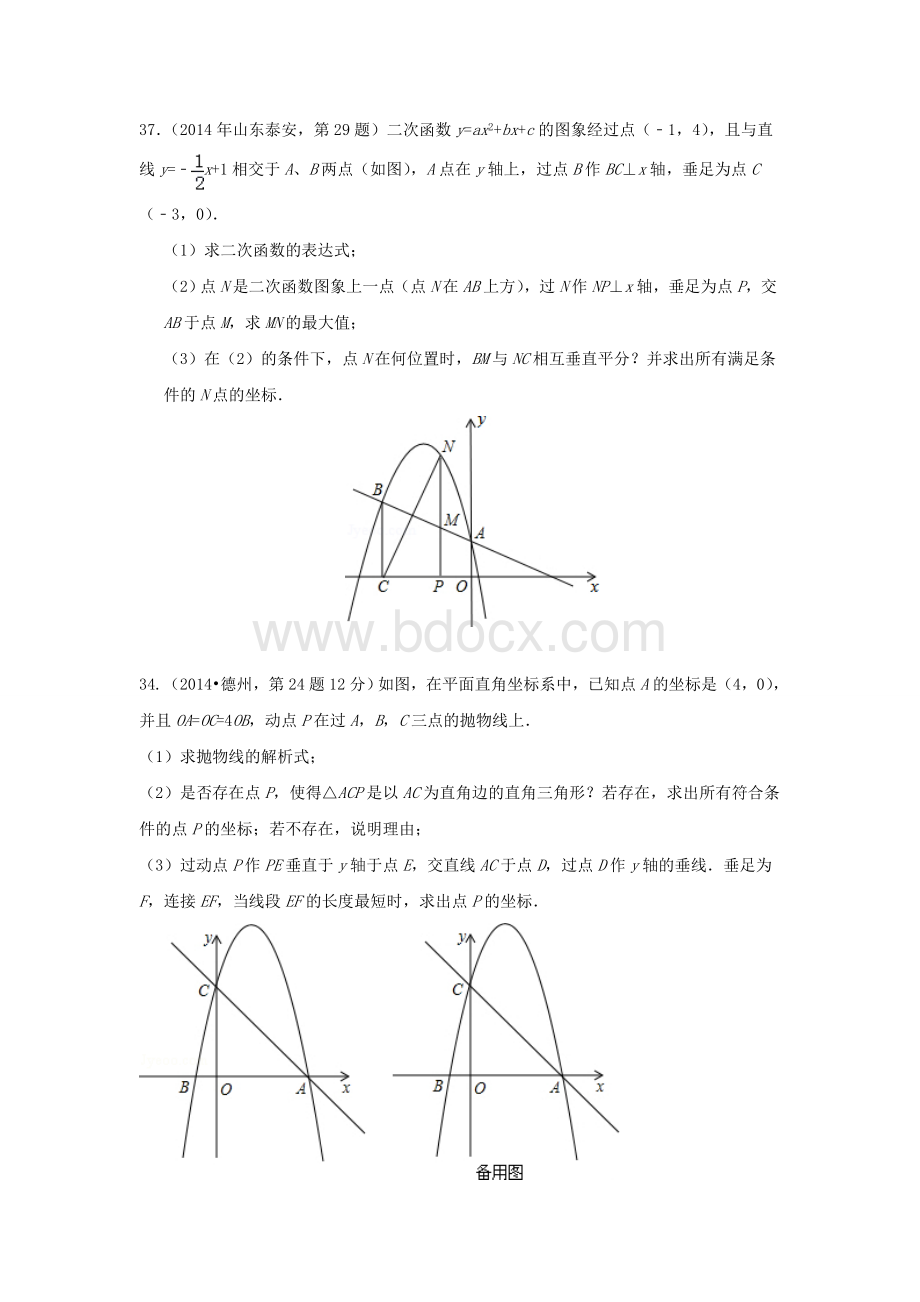
37．（2014年山东泰安，第29题）二次函数y=ax2+bx+c的图象经过点（﹣1，4），且与直线y=﹣x+1相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．

（1）求二次函数的表达式；

（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；

（3）在

（2）的条件下，点N在何位置时，BM与NC相互垂直平分？

并求出所有满足条件的N点的坐标．

34.（2014•德州，第24题12分）如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．

（1）求抛物线的解析式；

（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？

若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

（3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作y轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

28.（2014•株洲，第24题，10分）已知抛物线y=x2﹣（k+2）x+和直线y=（k+1）x+（k+1）2．

（1）求证：

无论k取何实数值，抛物线总与x轴有两个不同的交点；

（2）抛物线于x轴交于点A、B，直线与x轴交于点C，设A、B、C三点的横坐标分别是x1、x2、x3，求x1•x2•x3的最大值；

（3）如果抛物线与x轴的交点A、B在原点的右边，直线与x轴的交点C在原点的左边，又抛物线、直线分别交y轴于点D、E，直线AD交直线CE于点G（如图），且CA•GE=CG•AB，求抛物线的解析式．

（第5题图）

24.（2014•湘潭，第25题）△ABC为等边三角形，边长为a，DF⊥AB，EF⊥AC，

（1）求证：

△BDF∽△CEF；

（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系，并探究当m为何值时S取最大值；

（3）已知A、D、F、E四点共圆，已知tan∠EDF=，求此圆直径．

（第1题图）

20.（2014•邵阳，第26题10分）在平面直角坐标系xOy中，抛物线y=x2﹣（m+n）x+mn（m＞n）与x轴相交于A、B两点（点A位于点B的右侧），与y轴相交于点C．

（1）若m=2，n=1，求A、B两点的坐标；

（2）若A、B两点分别位于y轴的两侧，C点坐标是（0，﹣1），求∠ACB的大小；

（3）若m=2，△ABC是等腰三角形，求n的值．

18.（10分）（2014•孝感，第22题10分）已知关于x的方程x2﹣（2k﹣3）x+k2+1=0有两个不相等的实数根x1、x2．

（1）求k的取值范围；

（2）试说明x1＜0，x2＜0；

（3）若抛物线y=x2﹣（2k﹣3）x+k2+1与x轴交于A、B两点，点A、点B到原点的距离分别为OA、OB，且OA+OB=2OA•OB﹣3，求k的值．

解：

（1）由题设可知A（0，1），B（﹣3，），

则二次函数的解析式是：

y=﹣﹣x+1；

（2）设N（x，﹣x2﹣x+1），则M、P点的坐标分别是（x，﹣x+1），（x，0）．

∴MN=PN﹣PM=﹣x2﹣x+1﹣（﹣x+1）=﹣x2﹣x=﹣（x+）2+，

则当x=﹣时，MN的最大值为；

（3）连接MN、BN、BM与NC互相垂直平分，

即四边形BCMN是菱形，由于BC∥MN，即MN=BC，且BC=MC，

即﹣x2﹣x=，且（﹣x+1）2+（x+3）2=，解得：

x=1，

故当N（﹣1，4）时，MN和NC互相垂直平分．

分析：

（3）据垂线段最短，可得当OD⊥AC时，OD最短，即EF最短，根据等腰三角形的性质，D是AC的中点，则DF=OC，即可求得P的纵坐标，代入二次函数的解析式，即可求得横坐标，得到P的坐标．

解答：

则抛物线的解析式是：

y=﹣x2+3x+4；

（2）存在．

第一种情况，当以C为直角顶点时，过点C作CP1⊥AC，交抛物线于点P1．过点P1作y轴的垂线，垂足是M．∵∠ACP1=90°，∴∠MCP1+∠ACO=90°．

∵∠ACO+∠OAC=90°，∴∠MCP1=∠OAC．∵OA=OC，∴∠MCP1=∠OAC=45°∴∠MCP1=∠MP1C，∴MC=MP1，

设P（m，﹣m2+3m+4），则m=﹣m2+3m+4﹣4，

解得：

m1=0（舍去），m2=2．∴﹣m2+3m+4=6，即P（2，6）．

第二种情况，当点A为直角顶点时，过A作AP2，AC交抛物线于点P2，过点P2作y轴的垂线，垂足是N，AP交y轴于点F．∴P2N∥x轴，由∠CAO=45°，∴∠OAP=45°，

∴∠FP2N=45°，AO=OF．∴P2N=NF，

设P2（n，﹣n2+3n+4），则n=（﹣n2+3n+4）﹣1，

解得：

n1=﹣2，n2=4（舍去），∴﹣n2+3n+4=﹣6，

则P2的坐标是（﹣2，﹣6）．

综上所述，P的坐标是（2，6）或（﹣2，﹣6）；

（3）连接OD，由题意可知，四边形OFDE是矩形，则OD=EF．

根据垂线段最短，可得当OD⊥AC时，OD最短，即EF最短．

由

（1）可知，在直角△AOC中，OC=OA=4，

则AC==4，

根据等腰三角形的性质，D是AC的中点．

又∵DF∥OC，

∴DF=OC=2，

∴点P的纵坐标是2．

则﹣x2+3x+1=2，

解得：

x=，

∴当EF最短时，点P的坐标是：

（，0）或（，0）．

考点：

二次函数综合题

分析：

（1）由判别式△=（k+2）2﹣4×1×=k2﹣k+2=（k﹣）2+＞0，即可证得无论k取何实数值，抛物线总与x轴有两个不同的交点；

（2）由抛物线于x轴交于点A、B，直线与x轴交于点C，设A、B、C三点的横坐标分别是x1、x2、x3，可得x1•x2=，x3=﹣（k+1），继而可求得答案；

（3）由CA•GE=CG•AB，易得△CAG∽△CBE，继而可证得△OAD∽△OBE，则可得，又由抛物线与x轴的交点A、B在原点的右边，直线与x轴的交点C在原点的左边，又抛物线、直线分别交y轴于点D、E，可得OA•OB=，OD=，OE=（k+1）2，继而求得点B的坐标为（0，k+1），代入解析式即可求得答案．

解答：

（1）证明：

∵△=（k+2）2﹣4×1×=k2﹣k+2=（k﹣）2+，

∵（k﹣）2≥0，

∴△＞0，

∴无论k取何实数值，抛物线总与x轴有两个不同的交点；

（2）解：

∵抛物线于x轴交于点A、B，直线与x轴交于点C，设A、B、C三点的横坐标分别是x1、x2、x3，

∴x1•x2=，

令0=（k+1）x+（k+1）2，

解得：

x=﹣（k+1），

即x3=﹣（k+1），

∴x1•x2•x3=﹣（k+1）•=﹣（k+）2+，

∴x1•x2•x3的最大值为：

；

（3）解：

∵CA•GE=CG•AB，

∴，

∵∠ACG=∠BCE，

∴△CAG∽△CBE，

∴∠CAG=∠CBE，

∵∠AOD=∠BOE，

∴△OAD∽△OBE，

∴，

∵抛物线与x轴的交点A、B在原点的右边，直线与x轴的交点C在原点的左边，又抛物线、直线分别交y轴于点D、E，

∴OA•OB=，OD=，OE=（k+1）2，

∴OA•OB=OD，

∴，

∴OB2=OE，

∴OB=k+1，

∴点B（k+1，0），

将点B代入抛物线y=x2﹣（k+2）x+得：

（k+1）2﹣（k+2）（k+1）﹣=0，

解得：

k=2，

∴抛物线的解析式为：

y=x2﹣4x+3．

考点：

相似形综合题；二次函数的最值；等边三角形的性质；圆周角定理；解直角三角形

分析：

（1）只需找到两组对应角相等即可．

（2）四边形ADFE面积S可以看成△ADF与△AEF的面积之和，借助三角函数用m表示出AD、DF、AE、EF的长，进而可以用含m的代数式表示S，然后通过配方，转化为二次函数的最值问题，就可以解决问题．

（3）易知AF就是圆的直径，利用圆周角定理将∠EDF转化为∠EAF．在△AFC中，知道tan∠EAF、∠C、AC，通过解直角三角形就可求出AF长．

解答：

解：

（1）∵DF⊥AB，EF⊥AC，

∴∠BDF=∠CEF=90°．

∵△ABC为等边三角形，

∴∠B=∠C=60°．

∵∠BDF=∠CEF，∠B=∠C，

∴△BDF∽△CEF．

（2）∵∠BDF=90°，∠B=60°，

∴sin60°==，cos60°==．

∵BF=m，

∴DF=m，BD=．

∵AB=4，

∴AD=4﹣．

∴S△ADF=AD•DF

=×（4﹣）×m

=﹣m2+m．

同理：

S△AEF=AE•EF

=×（4﹣）×（4﹣m）

=﹣m2+2．

∴S=S△ADF+S△AEF

=﹣m2+m+2

=﹣（m2﹣4m﹣8）

=﹣（m﹣2）2+3．其中0＜m＜4．

∵﹣＜0，0＜2＜4，

∴当m=2时，S取最大值，最大值为3．

∴S与m之间的函数关系为：

S═﹣（m﹣2）2+3（其中0＜m＜4）．

当m=2时，S取到最大值，最大值为3．

（3）如图2，

∵A、D、F、E四点共圆，

∴∠EDF=∠EAF．

∵∠ADF=∠AEF=90°，

∴AF是此圆的直径．

∵tan∠EDF=，

∴tan∠EAF=．

∴=．

∵∠C=60°，

∴=tan60°=．

设EC=x，则EF=x，EA=2x．

∵AC=a，

∴2x+x=a．

∴x=．

∴EF=，AE=．

∵∠AEF=90°，

∴AF==．

∴此圆直径长为．

（2）∵抛物线y=x2﹣（m+n）x+mn（m＞n）过C（0，﹣1），

∴﹣1=mn，∴n=﹣，∵B（n，0），∴B（﹣，0）．

∵AO=m，BO=﹣，CO=1∴AC==，BC==，

AB=AO+BO=m﹣，

∵（m﹣）2=（）2+（）2，∴AB2=AC2+BC2，∴∠ACB=90°．

（3）∵A（m，0），B（n，0），C（0，mn），且m=2，

∴A（2，0），B（n，0），C（0，2n）．

∴AO=2，BO=|n|，CO=|2n|，

∴AC==，BC==|n|，AB=xA﹣xB=2﹣n．

①当AC=BC时，=|n|，解得n=2（A、B两点重合，舍去）或n=﹣2；

②当AC=AB时，=2﹣n，解得n=0（B、C两点重合，舍去）或n=﹣；

③当BC=AB时，|n|=2﹣n，

当n＞0时，n=2﹣n，解得n=，

当n＜0时，﹣n=2﹣n，解得n=﹣．

综上所述，n=﹣2，﹣，﹣，时，△ABC是等腰三角形．

解答：

解：

（1）由题意可知：

△=【﹣（2k﹣3）】2﹣4（k2+1）＞0，

即﹣12k+5＞0

∴．

（2）∵，

∴x1＜0，x2＜0．

（3）依题意，不妨设A（x1，0），B（x2，0）．

∴OA+OB=|x1|+|x2|=﹣（x1+x2）=﹣（2k﹣3），

OA•OB=|﹣x1||x2|=x1x2=k2+1，

∵OA+OB=2OA•OB﹣3，

∴﹣（2k﹣3）=2（k2+1）﹣3，

解得k1=1，k2=﹣2．

∵，

∴k=﹣2．