专题03 平行模型巩固练习基础冲刺中考几何专项复习解析版.docx

专题03 平行模型巩固练习基础冲刺中考几何专项复习解析版.docx

《专题03 平行模型巩固练习基础冲刺中考几何专项复习解析版.docx》由会员分享，可在线阅读，更多相关《专题03 平行模型巩固练习基础冲刺中考几何专项复习解析版.docx（4页珍藏版）》请在冰豆网上搜索。

专题03平行模型巩固练习基础冲刺中考几何专项复习解析版

平行模型巩固练习（基础）

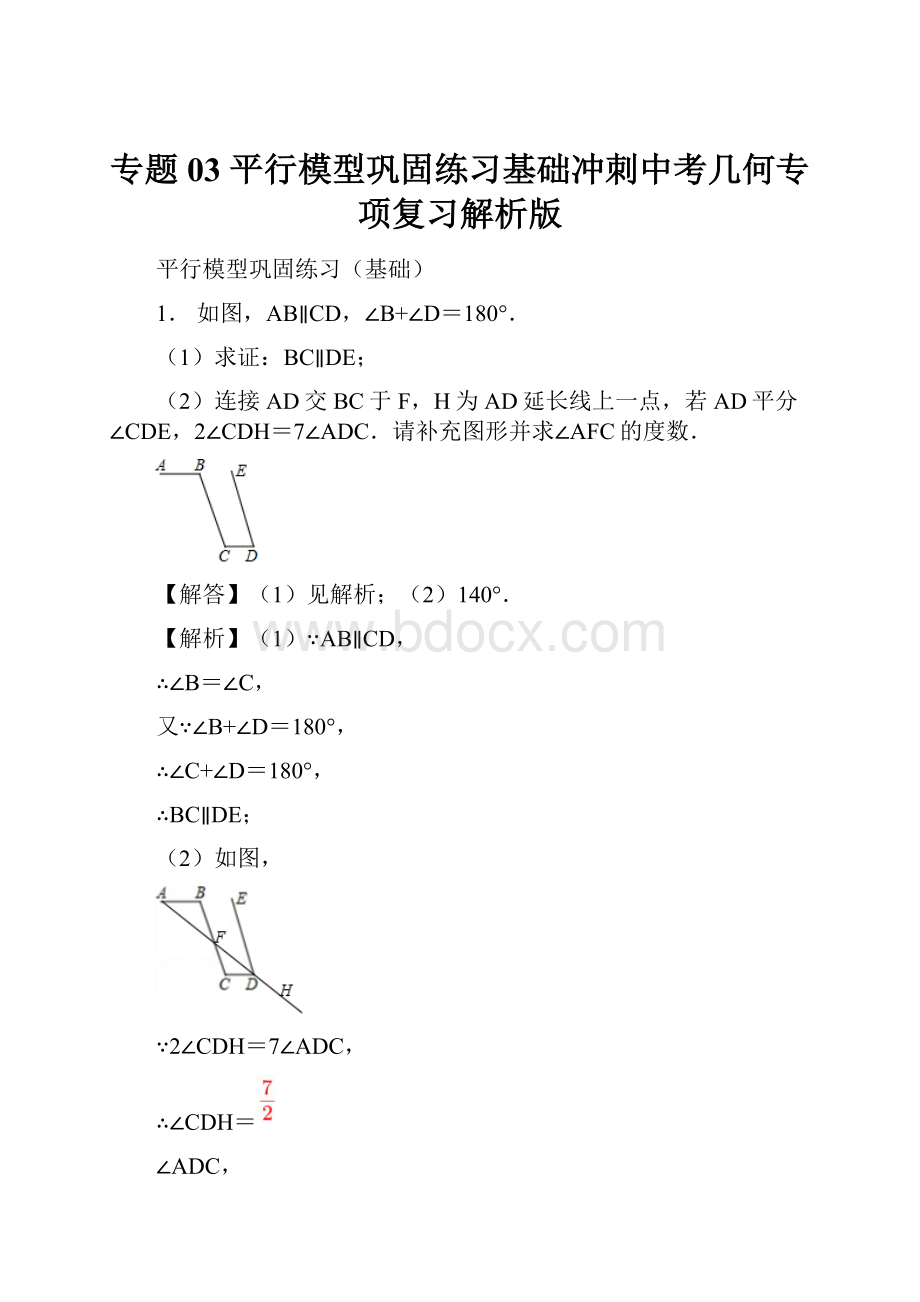
1．如图，AB∥CD，∠B+∠D＝180°．

（1）求证：

BC∥DE；

（2）连接AD交BC于F，H为AD延长线上一点，若AD平分∠CDE，2∠CDH＝7∠ADC．请补充图形并求∠AFC的度数．

【解答】

（1）见解析；

（2）140°．

【解析】

（1）∵AB∥CD，

∴∠B＝∠C，

又∵∠B+∠D＝180°，

∴∠C+∠D＝180°，

∴BC∥DE；

（2）如图，

∵2∠CDH＝7∠ADC，

∴∠CDH＝

∠ADC，

∵BC∥DE，

∴∠ADC+∠CDH＝180°，

∴

，

∴

，

∴∠ADC＝40°，

∵AD平分∠CDE，

∴∠CDE＝2∠ADC＝2×40°＝80°，

∵BC∥DE，

∴∠BCD+∠CDE＝180°，

∴∠BCD＝100°，

∴∠AFC＝∠BCD+∠CDA＝100°+40°＝140°．

2．如图，已知AB∥CF，∠ABC＝85°，∠CDE＝150°，∠BCD＝55°，求证：

CF∥DE．

【解答】见解析

【解析】证明：

∵AB∥CF，

∴∠BCF＝∠ABC＝85°，

∵∠BCD＝55°，

∴∠DCF＝∠BCF﹣∠BCD＝30°，

∵∠CDE＝150°，

∴∠CDE+∠DCF＝180°，

∴DE∥CF．

3．如图，点E在直线BH、DC之间，点A为BH上一点，且AE⊥CE，∠ECG＝90°﹣∠HAE．求证：

BH∥CD．

【解答】见解析

【解析】证明：

过点E作EF∥BH，

∴∠HAE＝∠AEF，

∵AE⊥CE，

∴∠AEC＝90°

即∠AEF+∠CEF＝90°，

∴∠HAE+∠CEF＝90°，

∴∠CEF＝90°﹣∠HAE，

∵∠ECG＝90°﹣∠HAE，

∴∠CEF＝∠ECG，

∴EF∥CD，

∵EF∥BH，

∴BH∥CD．

4．如图，CE⊥DG，垂足为C，∠BAF＝50°，∠ACE＝140°．试判断CD和AB的位置关系，并说明理由．

【解答】CD∥AB．

【解析】CD∥AB．

理由：

∵CE⊥DG，

∴∠ECG＝90°，

∵∠ACE＝140°，

∴∠ACG＝∠ACE﹣∠ECG＝50°，