材料力学期末考试复习题及答案.docx

材料力学期末考试复习题及答案.docx

《材料力学期末考试复习题及答案.docx》由会员分享，可在线阅读，更多相关《材料力学期末考试复习题及答案.docx（24页珍藏版）》请在冰豆网上搜索。

材料力学期末考试复习题及答案

二、计算题：

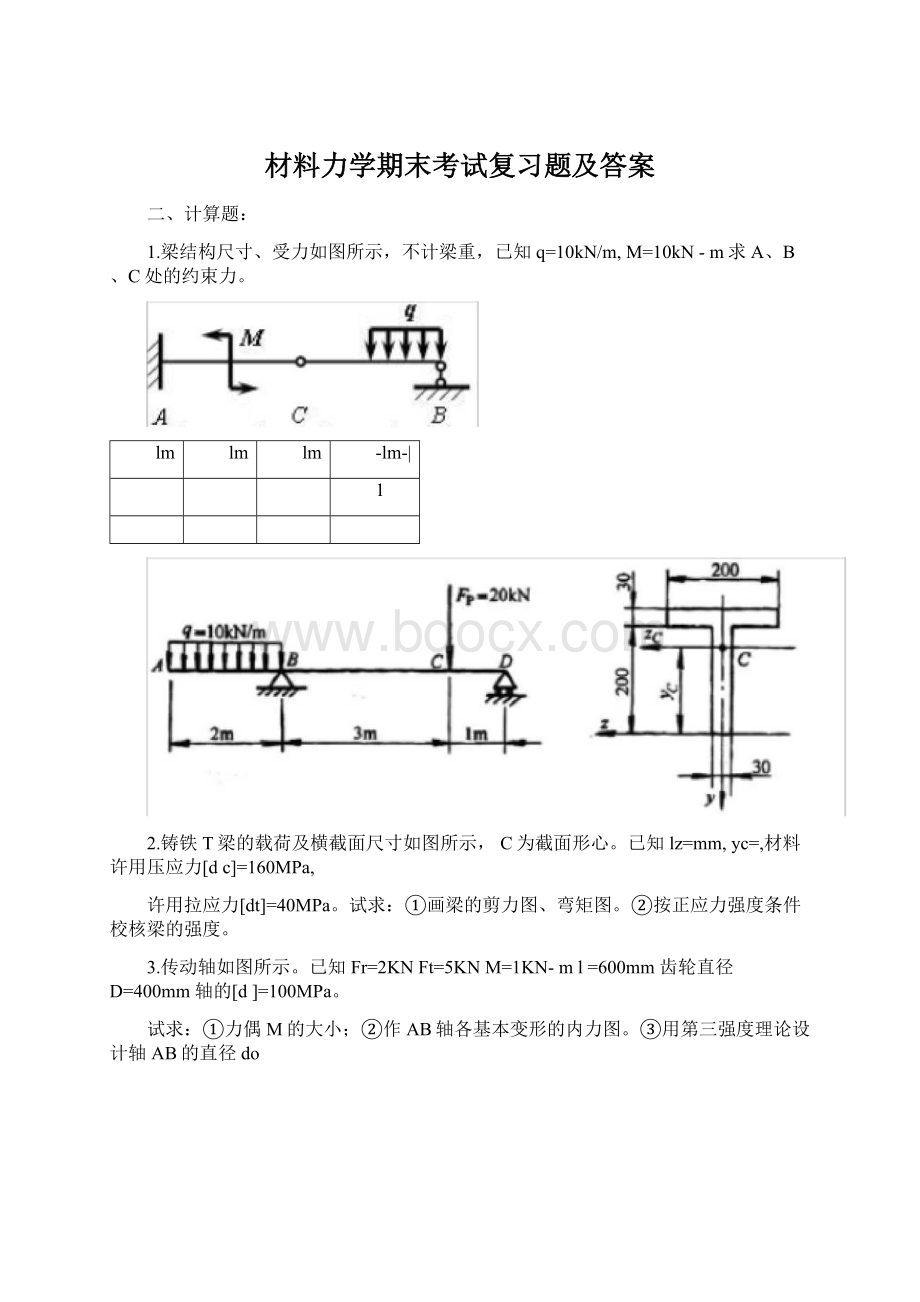
1.梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m,M=10kN-m求A、B、C处的约束力。

lm

lm

lm

-lm-|

1

2.铸铁T梁的载荷及横截面尺寸如图所示，C为截面形心。

已知lz=mm,yc=,材料许用压应力[dc]=160MPa,

许用拉应力[dt]=40MPa。

试求：

①画梁的剪力图、弯矩图。

②按正应力强度条件校核梁的强度。

3.传动轴如图所示。

已知Fr=2KNFt=5KNM=1KN-ml=600mm齿轮直径D=400mm轴的[d]=100MPa。

试求：

①力偶M的大小；②作AB轴各基本变形的内力图。

③用第三强度理论设计轴AB的直径do

4.图示外伸梁由铸铁制成，截面形状如图示。

已知Iz=4500cm,y1=,y2=,材料许用压应力[dc]=120MPa,

许用拉应力[dt]=35MPa,a=1m试求：

①画梁的剪力图、弯矩图。

②按正应力强度条件确定梁截荷P。

5.如图6所示，钢制直角拐轴，已知铅垂力F，水平力冃，实心轴AB的直径d,长度I，拐臂的长度a。

试求：

①作AB轴各基本变形的内力图。

②计算AB轴危险点的第三强度理论相当应力。

6.图所示结构，载荷P=50KkN,AB杆的直径d=40mm长度I=1000mm两端铰支。

已知材料E=200GPa

dp=200MPa（Ts=235MPaa=304MPab=，稳定安全系数nst=,[d]=140MPa。

试校核AB杆是否安全。

..4

7.铸铁梁如图5,单位为mm已知lz=10180cm，材料许用压应力[tc]=160MPa,许用拉应力[tt]=40MPa,

试求：

①画梁的剪力图、弯矩图。

②按正应力强度条件确定梁截荷P。

8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN-m的作用。

已知M=200GPa,口=,[t]=140MPa。

试求：

①作图示圆轴表面点的应力状态图。

②求圆轴表面点图示方向的正应变。

③按第四强度理论校核

圆轴强度。

9.图所示结构中,

q=20kN/m，柱的截面为圆形

d=80mm材料为Q235钢。

已知材料E=200GPatp=200MPa

ts=235MPaa=304MPab=，稳定安全系数

nst=,[t]=140MPa。

试校核柱BC是否安全。

10.如图所示的平面桁架,在铰链

H处作用了一个20kN的水平力，在铰链D处作用了一个60kN的垂直力。

求A、E处的约束力和FH杆的内力。

11.图所示圆截面杆件

用，材料的许用应力

d=80mm长度l=1000mm承受轴向力Fi=30kN,横向力F2=,外力偶M=700N-m的作

[d]=40MPa,试求：

①作杆件内力图。

②按第三强度理论校核杆的强度。

12.图所示三角桁架由

Q235钢制成，已知ABACBC为1m杆直径均为d=20mm已知材料E=200GPa

dp=200MPads=235MPaa=304MPab=,稳定安全系数nst=。

试由BC杆的稳定性求这个三角架所能承受的外载F。

13.槽形截面梁尺寸及受力图如图所示,

AB=3mB（=1m,z轴为截面形心轴,

84

Iz=x10mnr,q=15kN/m。

材料

许用压应力[dc]=160MPa,许用拉应力

[dt]=80MPa。

试求：

①画梁的剪力图、弯矩图。

②按正应力强度

条件校核梁的强度。

14.图所示平面直角刚架ABC在水平面xz内，AB段为直径d=20mm的圆截面杆。

在垂直平面内R=,在水平面内沿z轴方向F2=，材料的[d]=140MPa。

试求：

①作AB段各基本变形的内力图。

②按第三强度理论校核刚架AB段强度。

15.图所示由5根圆钢组成正方形结构，载荷P=50KkN,l=1000mm杆的直径d=40mm联结处均为铰链。

已知材料E=200GPa（TP=200MPa（Ts=235MPaa=304MPab=，稳定安全系数nst=,[©]=140MPa。

试校核1杆是否安全。

（15分）

q、a及B,不计梁的自重，求A、BC三处的约束力。

16.图所示为一连续梁，已知

17.图所示直径为d的实心圆轴，受力如图示，试求：

①作轴各基本变形的内力图。

②用第三强度理论导出此轴危险点相当应力的表达式。

18.如图所示，AB=800mmAC=600mmBC=1000mm杆件均为等直圆杆，直径d=20mm材料为Q235钢。

已

知材料的弹性模量E=200GPaTp=200MPaTs=235MPaa=304MPab=o压杆的稳定安全系数nst=3，试由CB杆的稳定性求这个三角架所能承受的外载Fo

参考答案

Mb（F）0：

1010.5Fc

2

0

Fy0:

FbFc101

0

解得：

Fb7.5kN

Fc2.5kN

以AC为研究对象，建立平衡方程

Fy0:

FAyFc0

Ma（F）0:

Ma10Fc2

0

解得：

FAy2.5kN

MA5kNm

解：

①求支座约束力，作剪力图

、弯矩图

Mb（F）0:

1021203

Fd4

Fy0:

FbFd102

200

解得：

Fb30kN

Fd10kN

WkM

+

-

2.

0

二、计算题：

1.解：

以CB为研究对象，建立平衡方程

②梁的强度校核

y1157.5mm

y2230157.572.5mm

拉应力强度校核

B截面

MBy2

tmax

Iz

2010372.5103

亍24.1MPa[t]

601250001012

33

McY11010157.510

tmax

Iz

60125000101226.2MPa[t]

压应力强度校核（经分析最大压应力在B截面）

MByi

cmax

Iz

2010157.51052.4MPa[c]

6012500010

所以梁的强度满足要求

3.解：

①以整个系统为为研究对象，建立平衡方程

D

2

Mx（F）0:

Ft

解得：

（3分）

FBz2.5kN

JliA-iu

FavFbv1kN

M1kNm

②求支座约束力，作内力图由题可得：

③由内力图可判断危险截面在C处

M2T2

r3W

32（M2dM：

）T2[]

32（MyMz）T

—:

5.1mm

[]

4.解：

①求支座约束力，作剪力图、弯矩图

Ma（F）

0：

FDy22P1P30

Fy0:

FavFdv2PP0

解得:

FAy2p

Fdv号p

95P

②梁的强度校核拉应力强度校核C截面

tmax

MCy2

Iz

0.5Pay2[

Iz

P

24.5kN

D截面

Md%

Payi

ri

tmax

1

1

t]

Iz

Iz

P

22.1kN

压应力强度校核（经分析取大压应力在

MDy2

Pay2

r1

cmax

1

1

c.

1z

1z

P

42.0kN

]

t]

D截面）

所以梁载荷P22.1kN

5.解：

①

6.解：

以

解得:

由内力图可判断危险截面在A处，该截面危险点在横截面上的正应力、切应力为

Fn

r3

M4F2

W"d1

16F,a

d3

32花界（F1）2

4F2

d2

CD杆为研究对象，建立平衡方程

Mc（F）0：

Fab93.75kN

AB杆柔度

由于

d3

32（F2a）2（FJ）

d3

2

）24（16d；a）2

d

0.8Fab0.6

丄3100

i40/4

2E

p，所以压杆

Fcr

crA

工作安全因数

所以AB杆安全

7.解：

①

500.9

2200109

200106

99.3

AB属于大柔度杆

2Ed2

2200109

1002

40a248.1kN

4

逊2.65

93.75

nst

②梁的强度校核

如96.4mm

y250

96.4153.6mm

tmax

Ma%

Iz

0.8P

Iz

y1

P

52.8kN

C截面

Mcy2

0.6P

y2

tmax

1

1

Iz

Iz

P

44.2kN

压应力强度校核（经分析

取大压

［应力

MAy2

0.8P

y2

cmax

1

1

1z

Iz

P

132.6kN

[

所以梁载荷P44.2kN

8.解：

①点在横截面上正应力、切应力

拉应力强度校核

A截面

t]

t]

c]

A截面）

3

47001089.1MPa

0.12

1661030.6MPa

0.13

点的应力状态图如下图:

WP

IW9.1V1lb3

严

3（1"IP®

-ycos2

2

xsin2

45o13.95MPa

45°

75.15MPa

由广义胡克定律

45°1（

③强度校核

450

45°）

1

200109

65

（13.950.375.15）104.297510

r4

■.89.12330.62

103.7MPa[]

所以圆轴强度满足要求

9.解：

以梁AD为研究对象，建立平衡方程

Ma（F）0:

Fab4205

2.50

解得:

Fbc

62.5kN

BC杆柔度

需200

p

p

2E

2200109

200106

99.3

由于

所以压杆BC属于大柔度杆

22

A

cr2

4

2200109

2002

26

80———248.1kN

工作安全因数

迴！

3.97

62.5

nst

所以柱BC安全

10.解：

以整个系统为研究对象,

建立平衡方程

解得:

Fx0：

Fy0：

Ma（F）

0:

Fex

200

FEy600

8203606

FEx20kN

FEy

52.5kN

7.5kN

过杆FHFCBC作截面，取左半部分为研究对象，建立平衡方程

12

Mc（F）0：

Fa『4Fhf0

5

解得：

Fhf12.5kN

11.解：

①

07k^-hi

切应力

i

E

p

p

200106

29

2001099.3

Fn

A

Mz

WZ

33

43010321.210

29.84MPa

0.082

0.085

T

16

700cc…r

6.96MPa