电路分析答案第三章.docx
《电路分析答案第三章.docx》由会员分享,可在线阅读,更多相关《电路分析答案第三章.docx(22页珍藏版)》请在冰豆网上搜索。
电路分析答案第三章
电路分析答案第三章
第三章习题
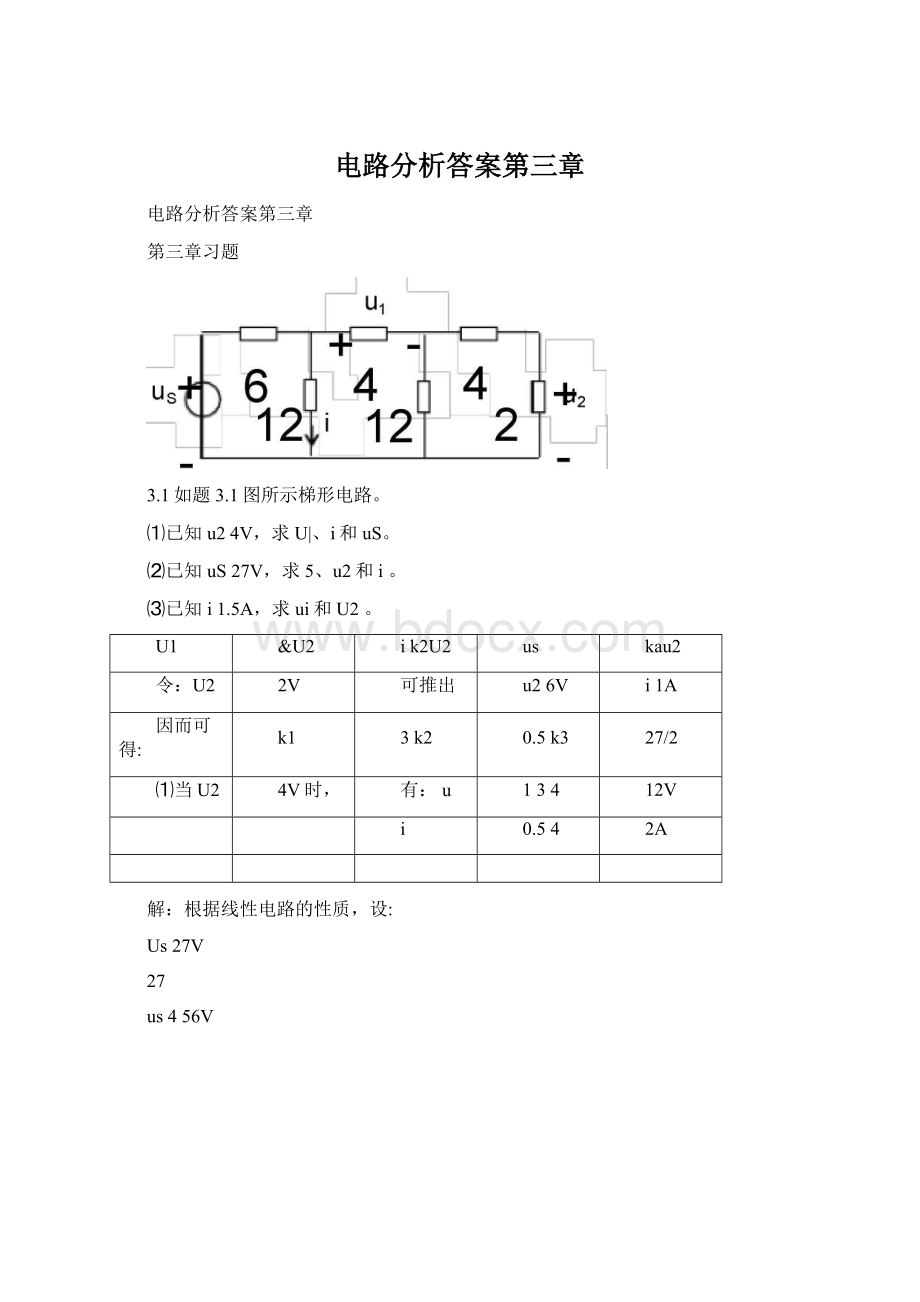
3.1如题3.1图所示梯形电路。
⑴已知u24V,求U|、i和uS。
⑵已知uS27V,求5、u2和i。
⑶已知i1.5A,求ui和U2。
U1
&U2
ik2U2
us
kau2
令:
U2
2V
可推出
u26V
i1A
因而可得:
k1
3k2
0.5k3
27/2
⑴当U2
4V时,
有:
u
134
12V
i
0.54
2A
解:
根据线性电路的性质,设:
Us27V
27
us456V
2
12
⑵当uS27V时,有:
u2丄us—27
kg27
独立电流源的值下降为原值的一半,电压u变为多少?
解:
根据KVL列一个回路
u3i11V3A2(3A2i1)4
两个电压源支路可列方程:
3ii1(3ii)610
由此可得:
ii3A
代入上式得:
u33132(323)44V
若独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,由上式可知:
3ii2(1.5ii)620解得ii3A
有:
u3321.52(1.523)44V
3.4如题3.4图所示电路,N为不含独立源的线性电路。
已知:
当us12V、
is4A时,u0V;当us12V、is2A时,u1V;求当us9V、is1A
时的电压u。
解:
根据线性电路的叠加定理,有:
u
皿k?
is
将已知数据代入,
有:
-012
k,4
lk2
1
12k1
2k
:
2
联立解得:
k
1
k2
1
6
2
因而有:
u
1us
1
i
s
将us9V
6s
2
可得:
u
丄9
丄(
1)
2V
6
2
is
+
1A代入
3.5
置2时,
解:
如题3.5图所示电路,
I=-60mA;求当s在位置3时的I值。
设电源Us和Is对电流I的贡献为|/,
已知当开关s在位置1时,l=40mA;当s在位
根据线性电路的叠加定理,有:
II/kU
其中U为开关外接电源的作用。
开关S在位置1时,
40I/
开关S在位置2时,
60I/
由上可解得:
k
当S在位置3时,U
Us+)
有
k0此时可将U视为0
有
4k
25I/40
6V,则有:
ls
R1
R3
R2
2)-4(花厂
+-
II/kU40256190mA
3.6如题3.6图所示电路,若ixi/8,求电阻Rx的值
解:
运用置换定理将电路变为如下图所示。
根据叠加定理电压Ux可看成电流源8ix和ix共同作用,即UxuXUx
uX由电流源8ix单独作用,u?
电流源ix单独作用根据分流关系,有:
/
158ix
10
8ix
Ux
5-
x5
24ix
16ix8ix
1510
15
10
//
Ux
[(10
5)//(5
5)]ix
15
10i6i
15
ix6ix
10
因而有:
Ux
///
UxUx
8ix6ix2ix
故得:
Rx
2
ix
i
3.7女口题3.7图所示电路,当
Rl分别为1Q、2Q和5Q时,求其上电流Il分
叠加原理,有:
Rl//2
Rl//22
Ul
UL1
UL2
10Rl//2
Rl〃22
2
整理可得:
U
L
6Rl
1Rl
当R
1
时,
有:
Il
Ul
6
3A
Rl
1
Rl
当R
2
时,
有
:
Il
Ul
6
2A
Rl
1
Rl
当R
1
时,
有:
Il
Ul
6
1A
Rl
1
Rl
别为多少?
解:
将电流源变换为电压源形式,再根据
3.8如题3.8图所示电路,N为不含独立源的线性电路,已知输出电压uUs/2;若在输出端接上5Q电阻,贝Uu输出电压u与输入电压US的关系如何?
解:
从输出端进行戴文宁等效,有
Rl/
uus
RsRl
uUs/2,可得u?
Us/2
UUs/3,代入上式可求得:
2.5
3时,有
Rl/3
Us
RsRl32.5
当Rl
当Rl
因此,
时,
5时,
R
当Rl
us/3。
问在输出端接3Q电阻时,
Us3
~211Us
Rs
/
Us
(+
□Rl
3.9
的3倍,
解:
如题3.9图所示电路,当R=12Q时其上电流为I。
若要求I增至原来值而电路中除R外的其他部分均不变,贝吐匕时的电阻R为多少?
从R两端进行戴文宁等效,可得等效
1
电源UsUs,等效电阻R03
6
根据等效电路,当
/
u_
R。
R
R12
1
-us
90
Ro,若I
3I,
则有:
1
-6Us
—632
-3—Us
90
3.10求如题3.10图所示各电路ab端的戴维宁等效电路和诺顿等效电路。
——2
>=i—
1•
1
Ui
解:
对图(a)电路进行诺顿等效,求ab两端的短路电流,如图可知:
1OC1112
24
Ii246A
4
243
6311636
1A
可得:
IocIiI27A
求电压源短路时,ab两端的等效电阻:
R04//(6//36)//82
对图(b)电路进行戴文宁等效,
■41—*■
3.11如题3.11(a)图所示线性有源二端电路N,其伏安关系如题3.11(b)图所
示。
试求它的戴维宁等效电路。
解:
根据戴文宁等效电路,端口电压、电流的约束关系为:
uUoc+Roi
当i0时,有Uoc-15V
当u0时,有R0^OC=0.5
i
i/A
「(
3.12如题3.12图所示线性时不变电阻电路,
时,电流iL[4cod(10t)2]A;当is4A、Rl
Rl10时,电流iL为多少?
解:
从负载两端进行诺顿等效,根据线性电路的齐次性,等效电流源为:
iSC
已知当iS2cos(10t)A、Rl
时,电流iL8A;问当iS
5A、
则有:
t=0时,
再将is
kis
R0
0kiS
R0RL
Rl2代入上式
R0.
iLiSC
R0RL
2A,il6A,
R01
2—k
R02
Rl4时,
4-^k
R04
4A、
iL
8A代入上式
联解①式和②式,可得:
6R02
Rl
因而有:
g2-
iL6is
2Rl
当is5A,
Rl10时,可得
2
iL655A
210
12V
等效电阻为:
R0=4//(26//3)2
则可得:
uR
UOCRR0
解得:
R4
3.14如题3.14图所示电路,N为含有独立源的线性电阻电路。
已知当Rl9时其上获得最大功率为1W,求N的戴维宁等效电路。
解:
将电路等效为如图所示,根据功率
最大传输定理,有:
u.,4PLmaxRL=6V
根据等效电路可知:
u(uOC-10)』+10
R0+10
解得:
uoc-30V或
uoc-150V
—n
4u+1OIIRo
o.1Ur、pIOU
—»
3.15如题3.15图所示电路,Rl可任意改变,问Rl等于多大时其上获得最
大功率,并求出该最大功率。
解:
对Rl两端进行戴文宁等效,首先求开路电压Uoc,有:
Uoc=25Ur+20
而Ur二(2-0.1Ur)10
解得Ur=10V可得:
Uoc=40V
再求等效电阻Ro,如右图所示,有:
U=5IUr
而此时Ur二(I-0.1Ur)10
解得UR=51
故得Ro=U=1O
根据最大功率传输定理,当Rl=Ro=1O时,可获得最大功率,为:
3.16如题3.16图所示电路,Us、Is均未知,已知当Rl4时电流L2A。
若Rl可任意改变,问Rl等于多大时其上获得最大功率,并求出该最大功率。
解:
从Rl两端进行戴文宁等效
可知RO2//2+1=2
又有Il啦代入已知数据
Ro+Rl
可得:
uOC12V
根据最大功率传输定理,有
当RlRo=2
时可获得最大功率
PLmax
UOC
4Rl
=122
=42
=18W
3.17如题3.17图所示电路,N为含独立源的线性电阻电路。
已知当受控电流源系数1时,电压U20V;当1时,电压U12.5/。
求为何值时外部电路从N获得最大功率,并求出该功率。
解:
将电路N进行戴文宁等效,并将受控源
转换为电压源形式,有
I1
UOC-1011得:
I1
20+10+R0
30+10
Uoc
+R0
20
1
I1
c
1
Il
又有:
u10I1+(20+10)I1
得:
I1
U
10
+30
R。
可得:
UOC
30+10+R0
U
10
+30
1
J10+>10I1
20V;
u12.5/代入,
20
UOC
40+R0
联立求解可得:
20
40
Uoc12・5
20+R020
Rl-:
UOC50V
R060
再求电路N的等效电阻Rl,用外加电压、电流法,
I1
U-10h
20+10
可求得:
RlU=30+10
11
10
+〉
10I1
当Rl
解得:
R0=60
时可获得最大功率,则有:
=3
RL=30+10=60
UOC502
PLmax」^==10.42W
4Rl460
3.18如题3.18图所示电路,Nr仅由线性电阻组成。
已知当时,i12A、U22V;当Us
最大功率为:
2A、U2
4Rl
10V、
Us6V、R22
R,4时,i13A,求此时的U2。
i
i
解:
设两组条件分别对应两个电路:
其中第一组条件对应图件对应图(b)。
求解变为对图(b)的电路,当u2
R24、U【1
(a),第二组条
10V、I;3A时,求
+2
设图r中有k个电阻,对图(a),第
个电阻上的电压、
电流分别为Ur和IRj;
对图(b),第j个电阻上的电压、电流分别为uRj和IRj。
根据欧姆定律,有
图(a)与图(b)具有相同的拓扑结构,根据特勒根定理,有
k
Usi(丨1)U2CURjiRj0
j1
k
uSi(ii)u2luRjiRj0
j1
kk
结合上面电阻Rj欧姆定律,有URjiRjuRjiRj
j1j1
因而可得
Us1(1()U2I2u;1(I1)u2i20
根据给出的已知条件,
由电路可知
12
u2/r2
2/2
1A
i2
u2/r2
u2/4
代入上式,有
6
(3)2
u2/4
10
(2)u210
解得
u2
4V
3.19如题3.19图所示电路中Nr仅由线性电阻组成,当11/端接电压源
解:
应用互易定理求解,互易后要保持拓扑结构不变,将图(a)变为如下
的电路图(c),并联一个2的电阻不影响电流i1,由置换定理将图(c)电路变为图(d)电路
Usi
ii
Nr
1/
/
i2
图
us1/220/2
iii1105
图(b)电路可以看成图(所以图(e)电路是图(d)电路。
显然有:
ii/
isi
10A
图
>1
15A
e)电路,电路的互易有:
1/
Nr
Us2
i2u1
is1us2
5
15
u1
30
解得:
u110V
根据互易定理形式二,
可得:
iRu1/25A
3.20如题3.20图所示电路,已知二端电路试求u、i和i1。
解:
对连接电路N的外电路进行戴文宁等效,可知等效电阻为
R0(1+1)//2=1
开路电压为(根据叠加定理):
.2Ui
Uoc
根据端口关系,代入可得方程解方程得:
当i1A,u
232
+2=2V
2+21+32+1
uuOC-R0i又已知
.2i
・/i
1V时,有
1A
+i-2
.//
i
-2A有u/
N端子上的电压电流关系为
当i-2A,u
2
2
4V时,有
i12(i
U)=1.5A
2u
i12(i)=3A
2
3.21如题3.21图所示电路中,若要求输出电压Uo不受电压源Us的影响,问受控源中的应为何值?
解:
从Ro两端进行戴文宁等效,如下图
所示,其开路电压为(将电流源变换为电压源,再根据叠加原理):
U1
鮎22
而
/2lsUs
U/U1+ss6+Us
2+2+6
2IsUs2Is-Us
U1ss2=ss
2+2+65
代入上式
可得:
/2IsUs
U/U1+ss6+Us=
_2Is-Us+
6Is-3Us
2+2+6
5
5
-(2Is-Us+6ls+2UJ
5
根据分压有:
Uo
+Us
若Uo不受Us的影响,
可得:
6
Ui
Ro
r/
/Ro1
UJ二-(2Is-Us+6ls+2UJ
Ro+R5R0+R
则应有:
Ro
7
Us+2Us=0
=2
+o
时,另
i;当R0时,支路B中的电流为iio。
设从N的左端试证,当R为任一值时,支路B中的电流
3.22如题3.22图所示某线性电路的支路A中接有电阻R。
当R一支路B中的电流i向右看进去的戴维宁等效电阻为Req。
iio
(io
RReq
RReq(i
io)
解:
将支路B电流i用电流源置换,则根据
线性电路的叠加定理,电路N左端的端口电压可表示为:
u=u/+kiu/为电路N内电源作用的分量
当R时,端口为开路电压u°c,有:
uOC=u/+ki
当R0时,端口电压为零,有:
Req
0=u/+ki0
可得:
uoc•,uoc
u二-.丨。
+
I-ioI-io
由戴文宁等效电路可知:
R
U=Uoc
R+Req
代入上式,可得:
1=(-+..)(ITo)io+-(iTo)
R+Reqoi-iOR+Req