初二数学压轴几何证明题含答案供参考.docx
《初二数学压轴几何证明题含答案供参考.docx》由会员分享,可在线阅读,更多相关《初二数学压轴几何证明题含答案供参考.docx(13页珍藏版)》请在冰豆网上搜索。
初二数学压轴几何证明题含答案供参考
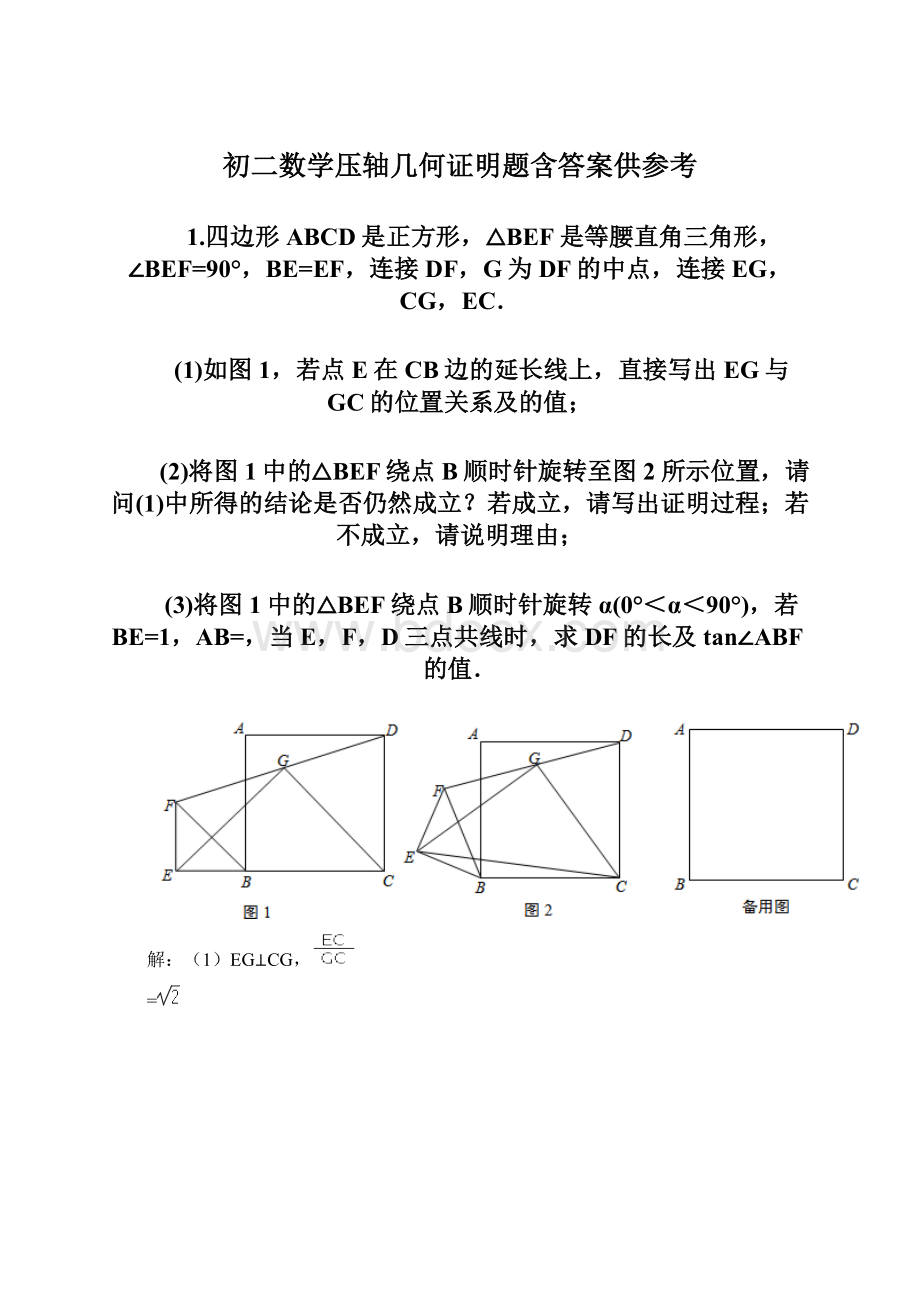
1.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及的值;
(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问
(1)中所得的结论是否仍然成立?
若成立,请写出证明过程;若不成立,请说明理由;
(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
解:
(1)EG⊥CG,
=
,
理由是:
过G作GH⊥EC于H,
∵∠FEB=∠DCB=90°,
∴EF∥GH∥DC,
∵G为DF中点,
∴H为EC中点,
∴EG=GC,GH=
(EF+DC)=
(EB+BC),
即GH=EH=HC,
∴∠EGC=90°,
即△EGC是等腰直角三角形,
∴
=
;
(2)
解:
结论还成立,
理由是:
如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,
∵在△EFG和△HDG中
∴△EFG≌△HDG(SAS),
∴DH=EF=BE,∠FEG=∠DHG,
∴EF∥DH,
∴∠1=∠2=90°-∠3=∠4,
∴∠EBC=180°-∠4=180°-∠1=∠HDC,
在△EBC和△HDC中
∴△EBC≌△HDC.
∴CE=CH,∠BCE=∠DCH,
∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°,
∴△ECH是等腰直角三角形,
∵G为EH的中点,
∴EG⊥GC,
=
,
即
(1)中的结论仍然成立;
(3)
解:
连接BD,
∵AB=
,正方形ABCD,
∴BD=2,
∴cos∠DBE=
=
,
∴∠DBE=60°,
∴∠ABE=∠DBE-∠ABD=15°,
∴∠ABF=45°-15°=30°,
∴tan∠ABF=
,
∴DE=
BE=
,
∴DF=DE-EF=
-1.
解析:
(1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,依照梯形的中位线求出EG=GC,GH=
(EF+DC)=
(EB+BC),推出GH=EH=BC,依照直角三角形的判定推出△EGC是等腰直角三角形即可;
(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△
HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案;
(3)连接BD,求出cos∠DBE=
=
,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.
2.已知正方形ABCD和等腰直角三角形BEF,BE=EF,∠BEF=90°,按图1放置,使点E在BC上,取DF的中点G,连接EG,CG.
(1)延长EG交DC于H,试说明:
DH=BE.
(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:
EG=CG且EG⊥CG.在设法证明时他发现:
若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?
请写出来.
(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?
若成立,试说明你的结论;若不成立,也请说明理由.
(1)证明:
∵∠BEF=90°,
∴EF∥DH,
∴∠EFG=∠GDH,
而∠EGF=∠DGH,GF=GD,
∴△GEF≌△GHD,
∴EF=DH,
而BE=EF,
∴
DH=BE;
(2)连接DB,如图,
∵△BEF为等腰直角三角形,
∴∠EBF=45°,
而四边形ABCD为正方形,
∴∠DBC=45°,
∴D,E,B三点共线.
而∠BEF=90°,
∴△FED为直角三角形,
而G为DF的中点,
∴EG=GD=GC,
∴∠EGC=2∠EDC=90°,
∴EG=CG且EG⊥CG;
(3)第2问中的结论成立.理由如下:
连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,
∵G为DF的中点,O为BD的中点,M为BF的中点,
∴OG∥BF,GM∥OB,
∴四边形OGMB为平行四边形,
∴OG=BM,GM=OB,
而EM=BM,OC=OB,
∴EM=OG,MG=OC,
∵∠DOG=∠GMF,
而∠DOC=∠EMF=90°,
∴∠EMG=∠GOC,
∴△MEG≌△OGC,
∴EG=CG,∠EGM=∠OCG,
又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,
∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,
∴EG=CG且EG⊥CG.
解析:
(1)由∠BEF=90°,取得EF∥DH,而GF=GD,易证得△GEF≌△GHD,得EF=DH,而BE=EF,即可取得结论.
(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,取得D,E,B三点共线,而G为DF的中点,依照直角三角形斜边上的中线等于斜边的一半取得EG=GD=GC,于是∠EGC=2∠EDC=90°,即取得结论.
(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,取得OG=BM,GM=OB,而EM=BM,OC=OB,取得EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF=90°,得∠EMG=∠GOC,那么△MEG≌△OGC,取得EG=CG,∠EGM=∠OCG,而∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,因此有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.
3.已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图①放置,使点F在BC上,取DF的中点G,连接EG、CG.
(1)探索EG、CG的数量关系和位置关系并证明;
(2)将图①中△BEF绕B点顺时针旋转45°,再连接DF,取DF中点G(如图②),问
(1)中的结论是否仍然成立.证明你的结论;
(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间),再连接DF,取DF的中点G(如图③),问
(1)中的结论是否仍然成立,证明你的结论.
解:
(1)EG=CG且EG⊥CG.
证明如下:
如图①,连接BD.
∵正方形ABCD和等腰Rt△BEF,
∴∠EBF=∠DBC=45°.
∴B、E、D三点共线.
∵∠DEF=90°,G为DF的中点,∠DCB=90°,
∴EG=DG=GF=CG.
∴∠EGF=2∠EDG,∠CGF=2∠CDG.
∴∠EGF+∠CGF=2∠EDC=90°,
即∠EGC=90°,
∴EG⊥CG.
(2)仍然成立,
证明如下:
如图②,延长EG交CD于点H.
∵BE⊥EF,∴EF∥CD,∴∠1=∠2.
又∵∠3=∠4,FG=DG,
∴△FEG≌△DHG,
∴EF=DH,EG=GH.
∵△BEF为等腰直角三角形,
∴BE=EF,∴BE=DH.
∵CD=BC,∴CE=CH.
∴△ECH为等腰直角三角形.
又∵EG=GH,
∴EG=CG且EG⊥CG.
(3)仍然成立.
证明如下:
如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.
∵GF=GD,∠HGF=∠CGD,HG=CG,
∴△HFG≌△CDG,
∴HF=CD,∠GHF=∠GCD,
∴HF∥CD.
∵正方形ABCD,
∴HF=BC,HF⊥BC.
∵△BEF是等腰直角三角形,
∴BE=EF,∠EBC=∠HFE,
∴△BEC≌△FEH,
∴HE=EC,∠BEC=∠FEH,
∴∠BEF=∠HEC=90°,
∴△ECH为等腰直角三角形.
又∵CG=GH,
∴EG=CG且EG⊥CG.
解析:
(1)第一证明B、E、D三点共线,依照直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG=GF=CG,取得∠EGF=2∠EDG,∠CGF=2∠CDG,从而证得∠EGC=90°;
(2)首先证明△FEG≌△DHG,然后证明△ECH为等腰直角三角形.能够证得:
EG=CG且EG⊥CG.
(3)首先证明:
△BEC≌△FEH,即可证得:
△ECH为等腰直角三角形,从而取得:
EG=CG且EG⊥CG.
已知,正方形ABCD中,△BEF为等腰直角三角形,且BF为底,取DF的中点G,连接EG、CG.
(1)如图1,假设△BEF的底边BF在BC上,猜想EG和CG的数量关系为______;
(2)
(2)如图2,假设△BEF的直角边BE在BC上,那么
(1)中的结论是不是还成立?
请说明理由;(3)如图3,假设△BEF的直角边BE在∠DBC内,那么
(1)中的结论是不是还成立?
说明理由.
1
2
1
2
解:
(1)GC=EG,(1分)理由如下:
∵△BEF为等腰直角三角形,
∴∠DEF=90°,又G为斜边DF的中点,∴EG=DF,
∵ABCD为正方形,
∴∠BCD=90°,又G为斜边DF的中点,∴CG=DF,
∴GC=EG;
(2)成立.如图,延长EG交CD于M,
1
2
∵∠BEF=∠FEC=∠BCD=90°,∴EF∥CD,
∴∠EFG=∠MDG,
又∠EGF=∠DGM,DG=FG,
∴△GEF≌△GMD,
∴EG=MG,即G为EM的中点.
∴CG为直角△ECM的斜边上的中线,
∴CG=GE=EM;
(3)成立.
取BF的中点H,连接EH,GH,取BD的中点O,连接OG,OC.
∵CB=CD,∠DCB=90°,∴CO=BD
1
2
1
2
.
∵DG=GF,
∴GH∥BD,且GH=BD,
1
2
OG∥BF,且OG=BF,
∴CO=GH.
1
2
∵△BEF为等腰直角三角形.
∴EH=BF
∴EH=OG.
∵四边形OBHG为平行四边形,
∴∠BOG=∠BHG.∵∠BOC=∠BHE=90°.
∴∠GOC=∠EHG.
∴△GOC≌△EHG.
∴EG=GC.
此题考查了正方形的性质,和全等三角形的判定与性质.要求学生把握直角三角形斜边上的中线等于斜边的一半,和三角形的中位线与第三边平行且等于第三边的一半.把握这些性质,熟练运用全等知识是解此题的关键.
解析:
(1)EG=CG,理由为:
依照三角形BEF为等腰直角三角形,取得∠DEF为直角,又G为DF中点,依照在直角三角形中,斜边上的中线等于斜边的一半,取得EG为DF的一半,同理在直角三角形DCF中,取得CG也等于DF的一半,利用等量代换得证;
(2)成立.理由为:
延长EG交CD于M,如下图,依照“ASA”取得三角形EFG与三角形GDM全等,由全等三角形的对应边相等取得EG与MG相等,即G为EM中点,依照直角三角形斜边上的中线等于斜边的一半取得EG与CG相等都等于斜边EM的一半,得证;
(3)成立.理由为:
取BF的中点H,连接EH,GH,取BD的中点O,连接OG,OC,如下图,因为直角三角形DCB中,O为斜边BD的中点,依照斜边上的中线等于斜边的一半取得OC等于BD的一半,由HG为三角形DBF的中位线,依照三角形的中位线平行于第三边且等于第三边的一半,取得GH等于BD一半,OG等于BF的一半,又依照直角三角形斜边上的中线等于斜边的一半取得EH等于BF的一半,依照等量代换取得OG与EH相等,再依照OBHG为平行四边形,依照平行四边形的性质取得对边相等,对角相等,进而取得∠GOC与∠EHG相等,利用“SAS”取得△GOC与△EHG全等,利用全等三角形的对应边相等即可得证.