网络计划优化案例.docx

网络计划优化案例.docx

《网络计划优化案例.docx》由会员分享，可在线阅读，更多相关《网络计划优化案例.docx（17页珍藏版）》请在冰豆网上搜索。

网络计划优化案例

网络计划优化示例

一、工期优化示例

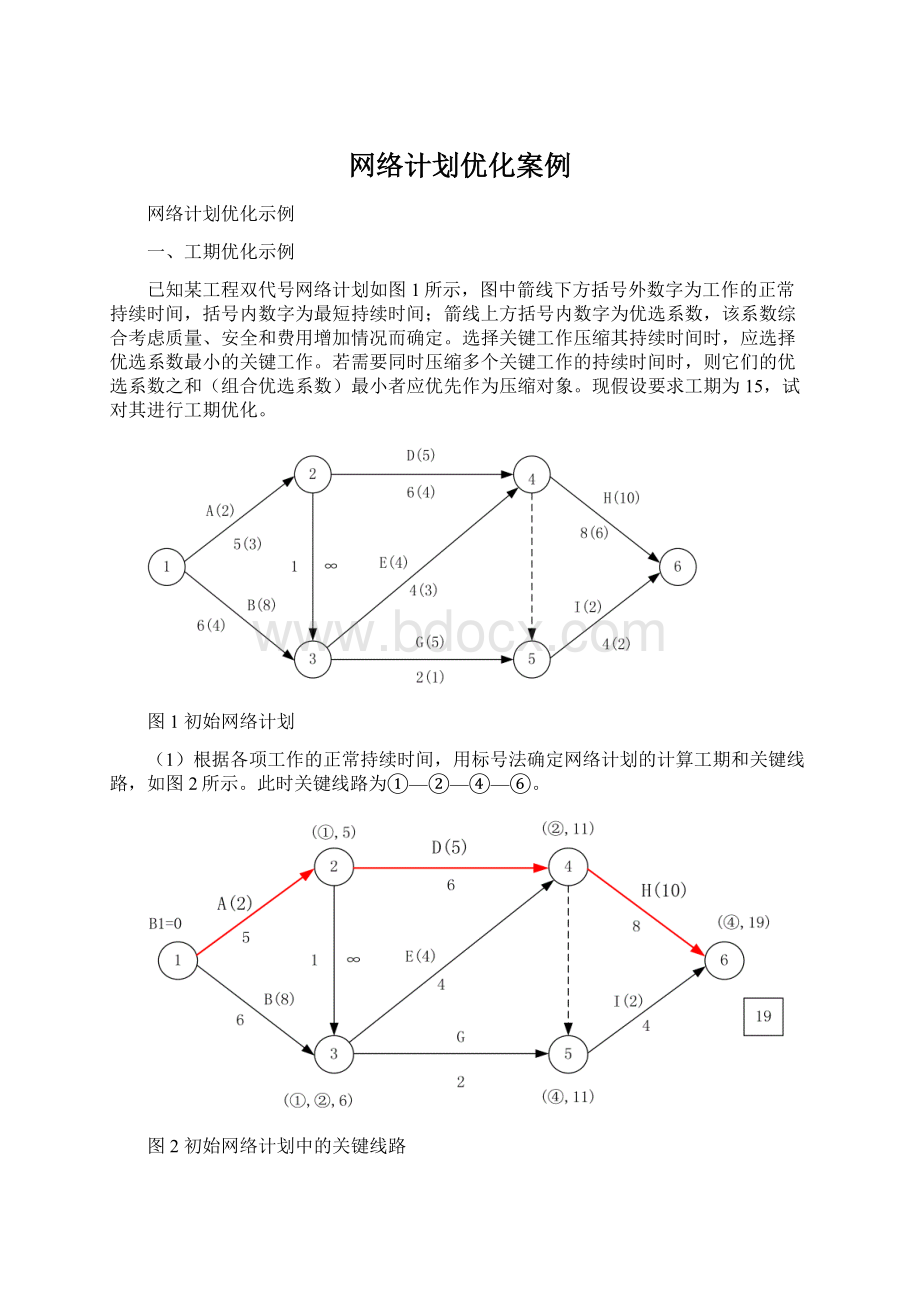
已知某工程双代号网络计划如图1所示，图中箭线下方括号外数字为工作的正常持续时间，括号内数字为最短持续时间；箭线上方括号内数字为优选系数，该系数综合考虑质量、安全和费用增加情况而确定。

选择关键工作压缩其持续时间时，应选择优选系数最小的关键工作。

若需要同时压缩多个关键工作的持续时间时，则它们的优选系数之和（组合优选系数）最小者应优先作为压缩对象。

现假设要求工期为15，试对其进行工期优化。

图1初始网络计划

（1）根据各项工作的正常持续时间，用标号法确定网络计划的计算工期和关键线路，如图2所示。

此时关键线路为①—②—④—⑥。

图2初始网络计划中的关键线路

（2）由于此时关键工作为工作A、工作D和工作H，而其中工作A酌优选系数最小，故应将工作A作为优先压缩对象。

（3）将关键工作A的持续时间压缩至最短持续时间3，利用标号法确定新的计算工期和关键线路，如图3所示。

此时，关键工作A被压缩成非关键工作，故将其持续时间3延长为4，使之成为关键工作。

工作A恢复为关键工作之后，网络计划中出现两条关键线路，即：

①—②—④—⑥和①—③—④—⑥，如图4所示。

图3工作A压缩至最短时间时的关键线路

图4第一次压缩后的网络计划

（4）由于此时计算工期为18，仍大于要求工期，故需继续压缩。

需要缩短的时间：

△T=18-15=3。

在图5所示网络计划中，有以下五个压缩方案：

①同时压缩工作A和工作B，组合优选系数为：

2+8=10；

②同时压缩工作A和工作E，组合优选系数为：

2+4=6；

③同时压缩工作B和工作D，组合优选系数为：

8+5=13；

④同时压缩工作D和工作E，组合优选系数为：

5+4=9；

⑤压缩工作H，优选系数为10。

在上述压缩方案中，由于工作A和工作E的组合优选系数最小，故应选择同时压缩工作A和工作E的方案。

将这两项工作的持续时间各压缩1（压缩至最短），再用标号法确定计算工期和关键线路，如图5所示。

此时，关键线路仍为两条，即：

①—②—④—⑥和①—③—④—⑥。

图5第二次压缩后的网络计划

在图5中，关键工作A和E的持续时间已达最短，不能再压缩，它们的优选系数变为无穷大。

（5）由于此时计算工期为17，仍大于要求工期，故需继续压缩。

需要缩短的时间：

△T2=17-15=2。

在图5所示网络计划中，由于关键工作A和E已不能再压缩，故此时只有两个压缩方案：

①同时压缩工作B和工作D，组合优选系数为：

8+5=13；

②压缩工作H，优选系数为10。

在上述压缩方案中，由于工作H的优选系数最小，故应选择压缩工作H的方案。

将工作H的持续时间缩短2，再用标号法确定计算工期和关键线路，如图6所示。

此时，计算工期为15，已等于要求工期，故图6所示网络计划即为优化方案。

图6工期优化后的网络计划

二、费用优化示例

已知某工程双代号网络计划如图7所示，图中箭线下方括号外数字为工作的正常时间，括号内数字为最短持续时间；箭线上方括号外数字为工作按正常持续时间完成时所需的直接费，括号内数字为工作按最短持续时间完成时所需的直接费。

该工程的间接费用率为0.8万元／天，试对其进行费用优化。

图7初始网络计划

（1）根据各项工作的正常持续时间，用标号法确定网络计划的计算工期和关键线路，如图8所示。

计算工期为19天，关键线路有两条，即：

①—③—④—⑥和①—③—④—⑤—⑥。

图8初始网络计划中的关键线路

（2）计算各项工作的直接费用率：

△C1-2=（7.4-7.0）∕（4-2）=0.2万元∕天

△C1-3=（11.0-9.0）∕（8-6）=1.0万元∕天

△C1-2=（7.4-7.0）∕（4-2）=0.2万元∕天

△C2-3=0.3万元∕天

△C2-4=0.5万元∕天

△C3-4=0.2万元∕天

△C3-5=0.8万元∕天

△C4-5=0.7万元∕天

△C4-6=0.5万元∕天

△C5-6=0.2万元∕天

（3）计算工程总费用：

①直接费总和：

Cd=7.0+9.0+5.7+5.5+8.0+8.0+5.0+7.5+6.5=62.2万元；

②间接费总和：

Ci=0.8×19=15.2万元；

③工程总费用：

Ct=Cd+Ci=62.2+15.2=77.4万元。

（4）通过压缩关键工作的持续时间进行费用优化（优化过程见表1）：

1）第一次压缩

从图8可知，该网络计划中有两条关键线路，为了同时缩短两条关键线路的总持续，有以下四个压缩方案：

1压缩工作B，直接费用率为1.0万元／天；

2压缩工作E，直接费用率为0.2万元／天；

3同时压缩工作H和工作I，组合直接费用率为：

0.7+0.5=1.2万元／天；

4同时压缩工作I和工作J，组合直接费用率为：

0.5+0.2=0.7万元／天。

在上述压缩方案中，由于工作E的直接费用率最小，故应选择工作E为压缩对象。

工作E的直接费用率0.2万元／天，小于间接费用率0，8万元／天，说明压缩工作E可使工程总费用降低。

将工作E的持续时间压缩至最短持续时间3天，利用标号法重新确定计算工期和关键线路，如图9所示。

此时，关键工作E被压缩成非关键工作，故将其持续时间延长为4天，使成为关键工作。

第一次压缩后的网络计划如图10所示。

图中箭线上方括号内数字为工作的直接费用率。

图9工作E压缩至最短时的关键线路

图10第一次压缩后的网络计划

2）第二次压缩

从图3-44可知，该网络计划中有三条关键线路，即：

①—③—④—⑥、①—③—④—⑤—⑥和①—③—⑤—⑥。

为了同时缩短三条关键线路的总持续时间，有以下五个压缩方案：

①压缩工作B，直接费用率为1.0万元／天；

②同时压缩工作E和工作G，组合直接费用率为0.2+0.8=1.0万元／天；

③同时压缩工作E和工作J，组合直接费用率为：

0.2+0.2=0.4万元／天；

④同时压缩工作G、工作H和工作J，组合直接费用率为：

0.8+0.7+0.5=2.0万元／天；

5同时压缩工作I和工作J，组合直接费用率为：

0.5+0.2=0.7万元／天。

在上述压缩方案中，由于工作E和工作J的组合直接费用率最小，故应选择工作E和工作J作为压缩对象。

工作E和工作J的组合直接费用率0.4万元／天，小于间接费用率0.8万元／天，说明同时压缩工作E和工作J可使工程总费用降低。

由于工作E的持续时间只能压缩1天，工作J的持续时间也只能随之压缩1天。

工作E和工作J的持续时间同时压缩1天后，利用标号法重新确定计算工期和关键线路。

此时，关键线路由压缩前的三条变为两条，即：

①—③—④—⑥和①—③—⑤—⑥。

原来的关键工作H未经压缩而被动地变成了非关键工作。

第二次压缩后的网络计划如图11所示。

此时，关键工作E的持续时间已达最短，不能再压缩，故其直接费用率变为无穷大。

图11第二次压缩后的网络计划

3）第三次压缩

从图11可知，由于工作E不能再压缩，而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间，只有以下三个压缩方案：

①压缩工作B，直接费用率为1.0万元／天；

②同时压缩工作G和工作I，组合直接费用率为0.8+0.5=1.3万元／天；

③同时压缩工作I和工作J，组合直接费用率为：

0.5+0.2=0.7万元／天。

在上述压缩方案中，由于工作I和工作J的组合直接费用率最小，故应选择工作I和工作J作为压缩对象。

工作I和工作J的组合直接费用率0.7万元∕天，小于间接费用率0.8万元∕天，说明同时压缩工作I和工作J可使工程总费用降低。

由于工作J的持续时间只能压缩1天，工作I的持续时间也只能随之压缩1天。

工作I和工作J的持续时间同时压缩l天后，利用标号法重新确定计算工期和关键线路。

此时，关键线路仍然为两条，即：

①—③—④—⑥和①—③—⑤—⑥。

第三次压缩后的网络计划如图12所示。

此时，关键工作／的持续时间也已达最短，不能再压缩，故其直接费用率变为无穷大。

图12第三次压缩后的网络计划

4）第四次压缩：

从图3-46可知，由于工作E和工作／不能再压缩，而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间，只有以下两个压缩方案：

①压缩工作B，直接费用率为1.O万元／天；

②同时压缩工作G和工作I，组合直接费用率为0.8+0.5=1.3万元∕天。

在上述压缩方案中，由于工作B的直接费用率最小，故应选择工作B作为压缩对象。

但是，由于工作B的直接费用率1.O万元∕天，大于间接费用率0.8万元／天，说明压缩工作B会使工程总费用增加。

因此，不需要压缩工作B，优化方案已得到，优化后的网络计划如图13所示。

图中箭线上方括号内数字为工作的直接费。

图13费用优化后的网络计划

（5）计算优化后的工程总费用

①直接费总和：

Cd0=7.0+9.0+5.7+5.5+8.4+8.0+5.0+8.0+6.9=63.5万元；

②间接费总和：

Ci0=0.8×16=12.8万元；

③工程总费用：

Ct0=Cd0+CiO=63.5+12.8=76.3万元。

优化表表1

压缩

次数

被压缩的工作代号

被压缩的工作名称

直接费用率

（万元/天）

费率差

（万元/天）

缩短

时间

（天）

费用

增加值

（万元）

总工期

（天）

总费用

（万元）

0

--

--

--

--

--

--

19

77.4

1

3-4

E

0.2

-0.6

1

-0.6

18

76.8

2

3-4

5-6

E、J

0.4

-0.4

1

-0.4

17

76.4

3

4-6

5-6

I、J

0.7

-0.1

1

-0.1

16

76.3

4

1-3

B

1.0

+0.2

--

--

--

--

三、资源优化

（一）“资源有限，工期最短”的优化

已知某工程双代号网络计划如图14所示，图中箭线上方数字为工作的资源强度，箭线下方数字为工作的持续时间。

假定资源限量Ra=12，试对其进行“资源有限，工期最短”的优化。

图14初始网络计划

（1）计算网络计划每个时间单位的资源需用量，绘出资源需用量动态曲线，如图14下方曲线所示。

（2）从计划开始日期起，经检查发现第二个时段[3，4]存在资源冲突，即资源需用量超过资源限量，故应首先调整该时段。

（3）在时段[3，4]有工作1-3和工作2-4两项工作平行作业，利用公式计算△T值，其结果见表2。

△T值计算表表2

序号

工作代号

最早完成时间

最迟开始时间

△T1，2

△T2，1

1

1-3

4

3

1

--

2

2-4

6

3

--

3

由表2可知，△T1，2=1最小，说明将第2号工作（工作2-4）安排在第1号工作（工作1-3）之后进行，工期延长最短，只延长1。

因此，将工作2-4安排在工作1-3之后进行，调整后的网络计划如图15所示。

图15第一次调整后的网络计划

（4）重新计算调整后的网络计划每个时间单位的资源需用量，绘出资源需用量动态曲线，如图15下方曲线所示。

从图中可知，在第四时段[7，9]存在资源冲突，故应调整该时段。

（5）在时段[7，9]有工作3-6、工作4-5和工作4-6三项工作平行作业，利用公式计算△T值，其结果见表3。

△T值计算表表3

序号

工作

代号

最早完成时间

最迟开始时间

△T1,2

△T1,3

△T2,1

△T2,3

△T3,1

△T3,2

1

3-6

9

8

2

0

2

4-5

10

7

2

1

3

4-6

11

9

3

4

由表3可知，△T1，3=0最小，说明将第3号工作（工作4-6）安排在第1号工作（工作3-6）之后进行，工期不延长。

因此，将工作4-6安排在工作3-6之后进行，调整后的网络计划如图16所示。

图16优化后的网络计划

（6）重新计算调整后的网络计划每个时间单位的资源需用量，绘出资源需用量动态曲线，如图16下方曲线所示。

由于此时整个工期范围内的资源需用量均未超过资源限量，故图16所示方案即为最优方案，其最短工期为13。

（二）“工期固定，资源均衡”的优化

已知某工程双代号网络计划如图17所示，图中箭线上方数字为工作的资源强度，箭线下方数字为工作的持续时间。

试对其进行“工期固定，资源均衡”的优化。

（1）计算网络计划每个时间单位的资源需用量，绘出资源需用量动态曲线，如图17下方曲线所示。

（2）第一次调整

1）以终点节点⑥为完成节点的工作有三项，即工作3-6、工作5-6和工作4-6。

其中工作5-6为关键工作，由于工期固定而不能调整，只能考虑工作3-6和工作4-6。

图17初始网络计划

由于工作4-6的开始时间晚于工作3-6的开始时间，应先调整工作4-6。

在图17中，按照判别式：

1由于R11+r4—6=9+3=12，R7=12，二者相等，故工作4-6可右移一个时间单位，改为第8个时间单位开始；

2于R12+r4-6=5+3=8，小于R8=12，故工作4-6可再右移一个时间单位，改为第9个时间单位开始；

3于R13+r4—6=5+3=8，小于R9=12，故工作4-6可再右移一个时间单位，改为第10个时间单位开始；

4于R14+r4-6=5+3=8，小于R10=12；故工作4-6可再右移一个时间单位，改为第11个时间单位开始。

至此，工作4-6的总时差已全部用完，不能再右移。

工作4-6调整后的网络计划如图18所示。

图18工作4-6调整后的网络计划

工作4-6调整后，就应对工作3-6进行调整。

在图18中，按照判别式：

1由于R12+r3—6=8+4=12，小于R5=20，故工作3-6可右移一个时间单位，改为第6个时间单位开始；

2于R13+r3-6=8+4=12，大于R6=8，故工作3-6不能右移一个时间单位；

3于R14+r3-6=8+4=12，大于R7=9，故工作3-6也不能右移两个时间单位。

由于工作3-6的总时差只有3，故该工作此时只能右移一个时间单位，改为第6个时间单位开始。

工作3-6调整后的网络计划如图19所示。

图19工作3-6调整后的网络计划

2）以节点⑤为完成节点的工作有两项，即工作2－5和工作4－5。

其中工作4－5为关键工作，不能移动，故只能调整工作2-5。

在图19中，按照判别式：

①由于R6+r2—5=8+7=15，小于R3=19，故工作2-5可右移一个时间单位，改为第4个时间单位开始；

②由于R7+r2—5=9+7=16，小于R4=19，故工作2-5可再右移一个时间单位，改为第5个时间单位开始；

4于R8+r2-5=9+7=16，R5=16，二者相等，故工作2-5可再右移一个时间单位，改为第6个时间单位开始；

5于R9+r2-5=9+7=16，大于R6=8，故工作2-5不可右移一个时间单位。

此时，工作2-5虽然还有总时差，但不能满足判别式，故工作2-5不能再右移。

至此，工作2-5只能右移3，改为第6个时间单位开始。

工作2-5调整后的网络计划如图20所示。

图20工作2-5调整后的网络计划

3）以节点④为完成节点的工作有两项，即工作1-4和工作2-4。

其中工作2-4为关键工作，不能移动，故只能考虑调整工作1-4。

在图20中，由于R6+r1—4=15+5=20，大于R1=14，不满足判别式，故工作1-4不可右移。

4）以节点③为完成节点的工作只有工作1-3，在图20中，由于R5+r1—3=9+3=12，小于R1=14，故工作1-3可右移一个时间单位。

工作1-3调整后的网络计划如图21所示。

图21工作1-3调整后的网络计划

5）以节点②为完成节点的工作只有工作1-2，由于该工作为关键工作，故不能移动。

至此，第一次调整结束。

（3）第二次调整：

从图21可知，在以终点节点⑥为完成节点的工作中，只有工作3-6有机动时间，有可能右移。

按照判别式：

①由于R13+r3—6=8+4=12，小于R6=15，故工作3-6可右移一个时间单位，改为第7个时间单位开始；

②由于R14+r3—6=8+4=12，小于R7=16，故工作3—6可再右移一个时间单位，改为第8个时间单位开始。

至此，工作3-6的总时差已全部用完，不能再右移。

工作3-6调整后的网络计划如图22所示。

图22优化后的网络计划

从图22可知，此时所有工作右移或右移均不能使资源需用量更加均衡。

因此，图22所示网络计划即为最优方案。