数学建模题01.docx
《数学建模题01.docx》由会员分享,可在线阅读,更多相关《数学建模题01.docx(19页珍藏版)》请在冰豆网上搜索。
数学建模题01
数学建模试题
一、地震预测模型
2008年5月12日发生在四川汶川的一场大地震给我们每一位中国人带来了巨大的伤痛,痛定思痛,我们应该为减少震后灾害做些事情。
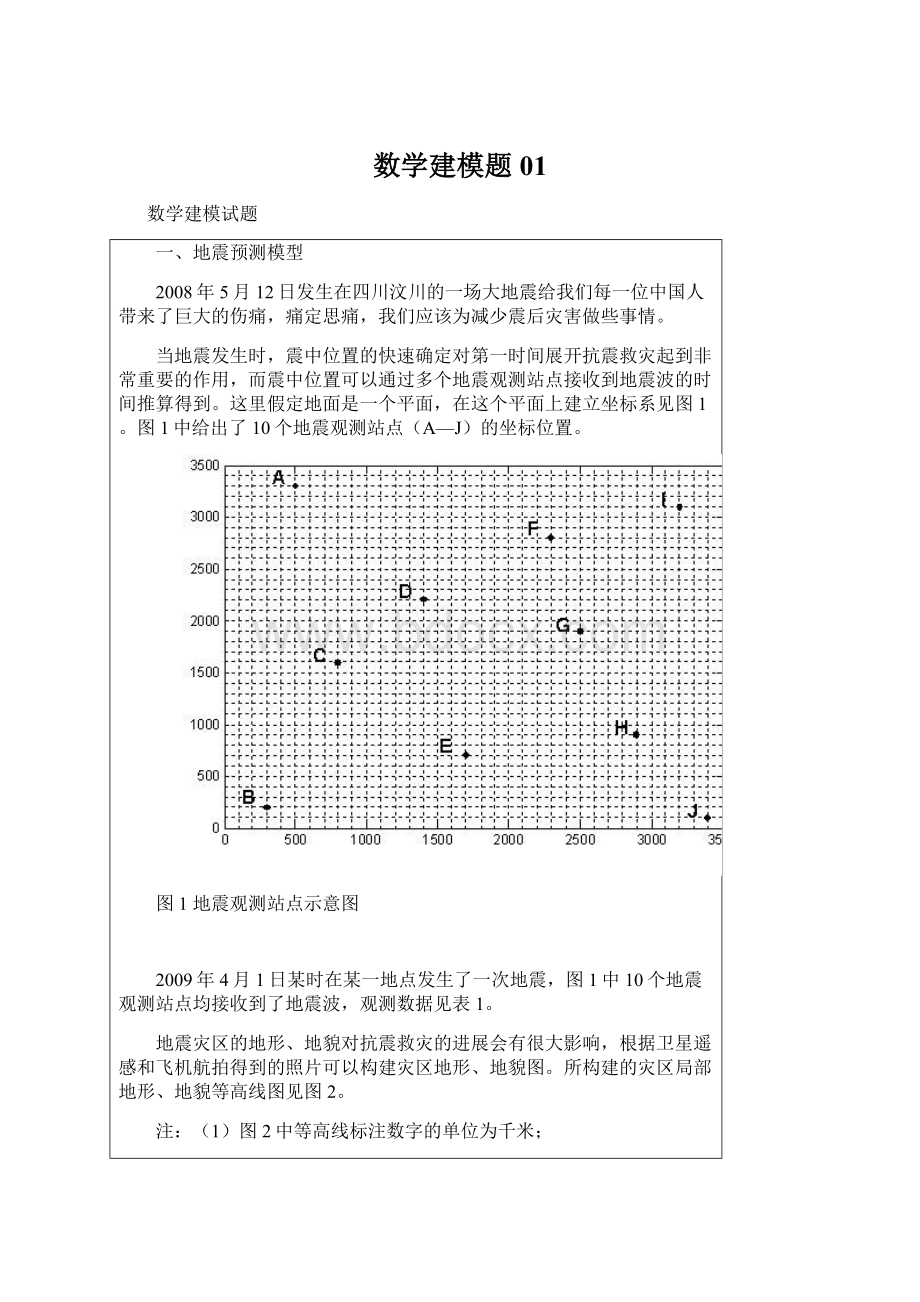
当地震发生时,震中位置的快速确定对第一时间展开抗震救灾起到非常重要的作用,而震中位置可以通过多个地震观测站点接收到地震波的时间推算得到。
这里假定地面是一个平面,在这个平面上建立坐标系见图1。
图1中给出了10个地震观测站点(A—J)的坐标位置。
图1地震观测站点示意图
2009年4月1日某时在某一地点发生了一次地震,图1中10个地震观测站点均接收到了地震波,观测数据见表1。
地震灾区的地形、地貌对抗震救灾的进展会有很大影响,根据卫星遥感和飞机航拍得到的照片可以构建灾区地形、地貌图。
所构建的灾区局部地形、地貌等高线图见图2。
注:
(1)图2中等高线标注数字的单位为千米;
(2)图1和图2不属于同一坐标系。
图2灾区局部地形、地貌等高线图
问题一:
假定地震波在各种介质和各个方向的传播速度均相等,并且在传播过程中保持不变。
请你根据表1中的数据确定这次地震的震中位置、震源深度以及地震发生的时间(不考虑时区因素,建议时间以分为单位)。
问题二:
请你根据图2中的局部地形、地貌等高线图,建立数学模型,绘制出相应的三维地形、地貌曲面图。
问题三:
查阅有关资料,了解地震波在各种介质和各个方向的传播速度问题,给出合理假设,根据表1中的数据确定这次地震的震中位置、震源深度以及地震发生的时间
表1地震观测站坐标及接收地震波时间
地震观测站
横坐标x(千米)
纵坐标y(千米)
接收地震波时间
A
500
3300
4月1日9时21分9秒
B
300
200
4月1日9时19分29秒
C
800
1600
4月1日9时14分51秒
D
1400
2200
4月1日9时13分17秒
E
1700
700
4月1日9时11分46秒
F
2300
2800
4月1日9时14分47秒
G
2500
1900
4月1日9时10分14秒
H
2900
900
4月1日9时11分46秒
I
3200
3100
4月1日9时17分57秒
J
3400
100
4月1日9时16分49秒
二、线性规划模型—销售计划问题
某商店拟制定某种商品7—12月的进货、售货计划,已知商店仓库最大容量为1500件,6月底已存货300件,年底的库存以不少于300件为宜,以后每月初进货一次,假设各月份该商品买进、售出单价如下表。
月
7
8
9
10
11
12
买进(元/件)
28
26
22.5
27
23
23.5
售出(元/件)
29
27
26
28
25
25
要求:
若每件每月的库存费用为0.5元,问各月进货、售货各为多少件,才能使净收益最多?
建立数学模型,并用软件求解。
【注】线性规划在MATLAB的库函数为:
linprog。
语法为:
x=linprog(f,A,b)
x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval,exitflag,output,lambda]=linprog(...)
例如:
线性规划目标函数的系数:
f=[-5;-4;-6]
约束方程的系数及右端项:
A=[1-11
324
320];
b=[20;42;30];lb=zeros(3,1);
调用线性规划程序linprog求解,得:
[x,fval,exitflag,output,lambda]=linprog(f,A,b,[],[],lb);
x=0.0000
15.0000
3.0000
三、一阶常微分方程模型—人口模型与预测
下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(
),
万人,
万人。
年
1982
1983
1984
1985
1986
1987
1988
1989
1990
人口
(万)
101654
103008
104357
105851
107507
109300
111026
112704
114333
年
1991
1992
1993
1994
1995
1996
1997
1998
人口
(万)
115823
117171
118517
119850
121121
122389
123626
124810
要求:
(1)建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic模型,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MATLAB图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
(4)利用MATLAB图形,画出两种预测模型的误差比较图,并分别标出其误差。
【注】常微分方程一阶初值问题的MATLAB库函数为:
ode45。
语法为:
[t,Y]=ode45(odefun,tspan,y0)
四、高阶常微分方程模型—饿狼追兔问题
现有一只兔子、一匹狼,兔子位于狼的正西110米处,假设兔子与狼同时发现对方并一起起跑,兔子往正北70米处的巢穴跑,而狼在追兔子。
已知兔子、狼是匀速跑且狼的速度是兔子的两倍。
要求:
(1)建立狼的运动轨迹微分模型。
(2)画出兔子与狼的运动轨迹图形。
(3)用解析方法求解,问兔子能否安全回到巢穴?
(4)用数值方法求解,问兔子能否安全回到巢穴?
【注】常微分方程高阶初值问题的MATLAB库函数为:
ode45。
语法为:
[t,Y]=ode45(odefun,tspan,y0)
例如函数:
functiondy=rigid(t,y)
dy=zeros(3,1);%acolumnvector
dy
(1)=y
(2)*y(3);
dy
(2)=-y
(1)*y(3);
dy(3)=-0.51*y
(1)*y
(2);
设置选项:
options=odeset('RelTol',1e-4,'AbsTol',[1e-41e-41e-5]);
求解得:
[t,Y]=ode45(@rigid,[012],[011],options);
画出解函数曲线图形:
plot(T,Y(:
1),'-',T,Y(:
2),'-.',T,Y(:
3),'.')
五、时间序列模型
某一商场1—11月份的销售额(单位:
万元)时间序列数据如下表所示。
月份
1
2
3
4
5
6
7
8
9
10
11
实际销售额
49
53
55
59
50
51
52
52
51
52
53
要求:
(1)建立恰当的数学模型,并预测下月(第12月)的销售额。
(2)对所建立的几种预测方法作误差的分析与比较。
【注】
(1)多项式拟合的MATLAB库函数为:
polyfit
语法为:
[p,S]=polyfit(x,y,n)
[p,S,mu]=polyfit(x,y,n)
例如:
x=(0:
0.1:
5)';
y=erf(x);
f=polyval(p,x);
plot(x,y,'o',x,f,'-')
axis([0502])
(2)自回归模型的MATLAB库函数为:
ar
语法为:
m=ar(y,n)
[m,refl]=ar(y,n,approach,window)
例如:
y=sin([1:
300]')+0.5*randn(300,1);
y=iddata(y);
mb=ar(y,4,'burg');
mfb=ar(y,4);
六、多元回归模型
根据经验,在人的身高相等的情况下,血压的收缩压
与体重
,年龄
有关,现在收集了13个男子的有关数据,如下表所示
数据表
76.0
91.5
85.5
82.5
79.0
80.5
74.5
79.0
85.0
76.5
82.0
95.0
92.5
50
20
20
30
30
50
60
50
40
55
40
40
20
120
141
124
126
117
125
123
125
132
123
132
155
147
要求:
(1)选择恰当的模型,建立收缩压
关于体重
和年龄
的关系模型。
并利用MATLAB画出曲线图形。
(2)设某男子的体重为83kg和年龄为32岁,预计该男子的血压的收缩压将是多少?
并对其作统计上的误差分析。
【注】多元线性回归模型的MATLAB库函数为:
regress。
语法为:
[b,bint,r,rint,stats]=regress(y,X);
例如:
loadmoore
X=[ones(size(moore,1),1)moore(:
1:
5)];
y=moore(:
6);
[b,bint,r,rint,stats]=regress(y,X);
七、整数规划模型
一家广告公司想在电视、广播上做广告,其目的是尽可能多的招揽顾客,下面是市场调查结果:
白天电视
电视黄金时间
无线电广播
杂志
一次广告费用(千元)
40
75
30
15
受每次广告影响的顾客数(千人)
400
900
500
200
受每次广告影响的女顾客数(千人)
300
400
200
100
这家公司希望广告费用不超过800千元,还要求:
(1)至少要有200万妇女收看广告
(2)电视广告费用不超过500千元
(3)电视广告白天至少播出3次,且最佳时间至少播出2次
(4)通过广播、电视做的广告要重复5到10次
八、高压锅的销售量
Logistic增长曲线模型和Gompertz增长曲线模型是计量经济学等学科中的两个常用模型,可以用来拟合销售量的增长趋势。
记Logistic增长曲线模型为
,记Gompertz增长曲线模型为
,这两个模型中L的经济意义都是销售量的上限。
表中给出的是某地区高压锅的销售量(单位:
万台)。
表高压锅的销售量(单位:
万台)
年份
t
y
年份
t
y
1981
0
43.65
1988
7
1238.75
1982
1
109.86
1989
8
1560.00
1983
2
187.21
1990
9
1824.29
1984
3
312.67
1991
10
2199.00
1985
4
496.58
1992
11
2438.89
1986
5
707.65
1993
12
2737.71
1987
6
960.25
要求:
(1)运用适当的方法,建立高压锅的销售量模型,并作出模型的分析与检验。
(2)Logistic增长曲线模型是一个可线性化模型吗?
如果是可线性化模型,取L=3000,建立Logistic的线性回归模型。
利用线性回归模型所得到的a和k的估计值和L=3000作为Logistic模型的拟合初值,对Logistic模型做非线性回归。
(3)拟合Gompertz模型。
(4)将几个模型作出比较与分析。
九、轿车更新问题
某人打算购买一辆新轿车,轿车的售价是12万元人民币。
轿车购买后,每年的各种保险费、养护费等费用如表1所示。
如果在5年之内将轿车售出,并再购买新车,5年之内的二手车销售价由表2所示。
请设计一种购买轿车的方案,使5年内用车的总费用最少。
表1轿车的维护费
车龄/年01234
费用/万元245912
表2二手车的售价
车龄/年12345
费用/万元76210
【注】此问题的求解利用最短路方法或动态规划方法。
十、航空机票超订票问题
某航空公司执行两地的飞行任务。
已知飞机的有效载客量为150人。
按民用航空管理有关规定:
旅客因有事或误机,机票可免费改签一次,此外也可在飞机起飞前退票。
航空公司为了避免由此发生的损失,采用超量订票的方法,即每班售出票数大于飞机载客数。
但由此会发生持票登机旅客多于座位数的情况,在这种情况下,航空公司让超员旅客改乘其它航班,并给旅客机票价的20%作为补偿。
要求:
(1)假设两地的机票价为1500元,每位旅客有0.04的概率发生有事、误机或退票的情况,问航空公司多售出多少张票,使该公司的预期损失达到最小?
(2)上述参数不变的情况下,问航空公司多售出多少张票,使该公司的预期利润达到最大,最大利润为多少?
十一、宠物店卖小狗的问题
背景:
一家宠物店卖小狗。
这家店每天需要在每只小狗身上花费10元钱,因此宠物店不想在店里存储太多的小狗。
通过调查研究,在给定的天数x内,所卖出的小狗的数量服从泊松分布(λ =0.1)。
宠物店每十天平均能卖出一只小狗,而每卖出一只小狗的利润是20元。
当一个顾客来到宠物店里时,如果店里没有宠物卖,那么该顾客就会到别的宠物店去。
如果宠物店预定小狗的话,则所预定的小狗需要到6天后才能到店里。
现在该宠物店正在考虑一种预定小狗的最好策略。
策略A:
每卖出一只小狗,宠物店就新预定一只。
这个策略意味着每次店里只有一个小狗,因此宠物店就不会花费太多在小狗身上。
策略B:
宠物店每隔10天就预定一只新的小狗,该狗6天后到。
使用这个策略后,如果顾客连续几个星期没有光顾宠物店,则宠物店必须花大量的钱在小狗上。
要求:
(1)用MATLAB编写程序,来模拟这两种策略,并比较哪一种策略好。
(2)请提出第三种更好的策略,写出数学证明, 并用MATLAB模拟。
十二、传染病的传播问题
SARS(SevereAcuteRespiratorySyndrome,严重急性呼吸道综合症,俗称:
非典型肺炎)是21世纪第一个在世界范围内传播的传染病。
SARS的爆发和蔓延给我国的经济发展和人民生活带来了很大影响,我们从中得到了许多重要的经验和教训,认识到定量地研究传染病的传播规律、为预测和控制传染病蔓延创造条件的重要性。
表疫情的数据
日期
已确诊病例累计
现有疑似病例
死亡累计
治愈出院累计
4月20日
339
402
18
33
4月21日
482
610
25
43
4月22日
588
666
28
46
4月23日
693
782
35
55
4月24日
774
863
39
64
4月25日
877
954
42
73
4月26日
988
1093
48
76
4月27日
1114
1255
56
78
4月28日
1199
1275
59
78
4月29日
1347
1358
66
83
4月30日
1440
1408
75
90
5月1日
1553
1415
82
100
5月2日
1636
1468
91
109
5月3日
1741
1493
96
115
5月4日
1803
1537
100
118
5月5日
1897
1510
103
121
5月6日
1960
1523
107
134
5月7日
2049
1514
110
141
5月8日
2136
1486
112
152
5月9日
2177
1425
114
168
5月10日
2227
1397
116
175
5月11日
2265
1411
120
186
5月12日
2304
1378
129
208
5月13日
2347
1338
134
244
5月14日
2370
1308
139
252
5月15日
2388
1317
140
257
5月16日
2405
1265
141
273
5月17日
2420
1250
145
307
5月18日
2434
1250
147
332
5月19日
2437
1249
150
349
5月20日
2444
1225
154
395
5月21日
2444
1221
156
447
5月22日
2456
1205
158
528
5月23日
2465
1179
160
582
5月24日
2490
1134
163
667
5月25日
2499
1105
167
704
5月26日
2504
1069
168
747
5月27日
2512
1005
172
828
5月28日
2514
941
175
866
5月29日
2517
803
176
928
5月30日
2520
760
177
1006
5月31日
2521
747
181
1087
6月16日
2521
3
190
2053
6月17日
2521
5
190
2120
6月18日
2521
4
191
2154
6月19日
2521
3
191
2171
6月20日
2521
3
191
2189
6月21日
2521
2
191
2231
6月22日
2521
2
191
2257
6月23日
2521
2
191
2277
6月1日
2522
739
181
1124
6月2日
2522
734
181
1157
6月3日
2522
724
181
1189
6月4日
2522
718
181
1263
6月5日
2522
716
181
1321
6月6日
2522
713
183
1403
6月8日
2522
550
184
1543
6月9日
2522
451
184
1653
6月10日
2522
351
186
1747
6月13日
2522
71
187
1944
6月14日
2522
4
189
1994
6月15日
2522
3
189
2015
6月7日
2523
668
183
1446
6月11日
2523
257
186
1821
6月12日
2523
155
187
1876
要求:
(1)建立传染病传播的指数模型,评价其合理性和实用性。
(2)建立一个适合的模型,说明为什么优于问题1中的模型;特别要说明怎样才能建立一个真正能够预测以及能为预防和控制提供可靠、足够的信息的模型,这样做的困难在哪里?
对于卫生部门所采取的措施做出评论,如:
提前或延后5天采取严格的隔离措施,对疫情传播所造成的影响做出估计。
表中提供的数据供参考。
(3)说明建立传染病数学模型的重要性。
十三、国土面积问题
为了算出瑞士的国土面积,首先对瑞士地图作如下测量:
以由西向东方向为
轴,由南到北方向为
轴,选择方便的原点,并将从最西边界点到最东边界点在
轴上的区间适当地划分为若干段,在每个分点的
方向测出南边界点和北边界点的
坐标
和
,这样就得到了表中的数据(单位mm)。
根据地图的比例我们知道18mm相当于40km,试由测量数据计算瑞士国土的近似面积,与它的精确值41288km
比较。
表瑞士地图测量数据
7.010.513.017.534.040.544.548.056.061.068.576.580.591.0
4445475050383030343634414546
4459707293100110110110117118116118118
96101104106.5111.5118123.5136.5142146150157158
43373328326555545250666668
121124121121121122116838182868568
十四、生产计划安排
某厂用一套设备生产若干种产品。
工厂靠银行贷款筹集资金,根据市场需求安排生产,现考虑以下的简化情形:
设生产甲乙两种产品,市场对它们的需求分别为d1,d2(件/天),该设备生产它们的最大能力分别为U1,U2(件/天),生产成本分别为c1,c2(元/件)。
当改变产品时因更换零部件等引起的生产甲乙前的准备费用分别为s1,s2(元)。
生产出的产品因超过当天的需求而导致的贮存费用,按生产成本的月利率r引起的积压资金的k倍计算(每月按30天计)。
问题1:
设每种产品的生产率都可以从零到最大能力之间连续调节,每种产品当前的需求均需满足。
请您为工厂制订合理、易行的生产计划,使上面考虑到的费用之和尽可能小。
1)
考虑有n种产品的情形,自行给出一组数据进行计算,讨论模型有解的条件。
提示:
考虑稳定的、周期性的计划(不必考虑初始情况)
十五、种群的繁殖与稳定收获
种群的数量因繁殖而增加,因自然死亡而减少,对于人工饲养的种群(比如家畜)而言,为了保证稳定的收获,各个年龄的种群数量应维持不变。
种群因雌性个体的繁殖而改变,为方便起见以下种群数量均指其中的雌性。
种群年龄记作
当年年龄
的种群数量记作
,繁殖率记作
(每个雌性个体一年繁殖的数量),自然存活率记作
为一年的死亡率),收获量记作
,则来年年龄
的种群数量
应为
要求:
(1)若
已知,给定收获量
,建立求各年龄的稳定种群数量
的模型(用矩阵、向量表示)。
(2)设
如要求
为500,400,200,100,100,求
。
十六、血样的分组检验
在人群(数量很大)中进行血样检验,设已知先验阳性率为p,为减少检验次数将人群分组。
若k人一组,当k份血样混在一起时,只要一份呈阳性,这组血样就呈阳性,则该组需人人检验;若一组血样呈阴性,则该组不需检验。
1)当p固定时(0.1%,1%,…),k多大可使检验次数最小
2)p多大就不应再分组
3)讨论两次分组的情况,即阳性组再分组检验。
4)讨论其它分组方案,如半分法、三分法。
十七、人口增长的年龄结构模型
不同年龄的人在死亡和生育方面存在着差异,下面三个表给出了某个国家在1966年人口统计资料,它的年龄区间长度为5年。
表1女婴出生率
年龄组
5~10
10~15
15~20
20~25
25~30
30~35
35~40
40~45
45~50
比率
0.00102
0.08515
0.30574
0.40002
0.28061
0.15260
0.06420
0.01483
0.00089
表2女性人口存活率
年龄组
比率
年龄组