浸出和萃取.docx
《浸出和萃取.docx》由会员分享,可在线阅读,更多相关《浸出和萃取.docx(27页珍藏版)》请在冰豆网上搜索。
浸出和萃取
第9章浸出和萃取浸出和萃取是指加溶剂于混合物,利用溶剂对不同物质具有不同溶解度,从而使混合物得到完全或部分分离的过程。
如果被处理的混合物为固体,则称为浸出或浸取;如果被处理的混合物为液体,则称为液—液萃取或萃取。
分离的依据:
组分的溶解度不同。
1浸出
1.1浸出理论
1.1.1浸出体系组成的表示方法
浸出体系为三组分体系:
①溶质A;②溶剂S;③惰性固体B。
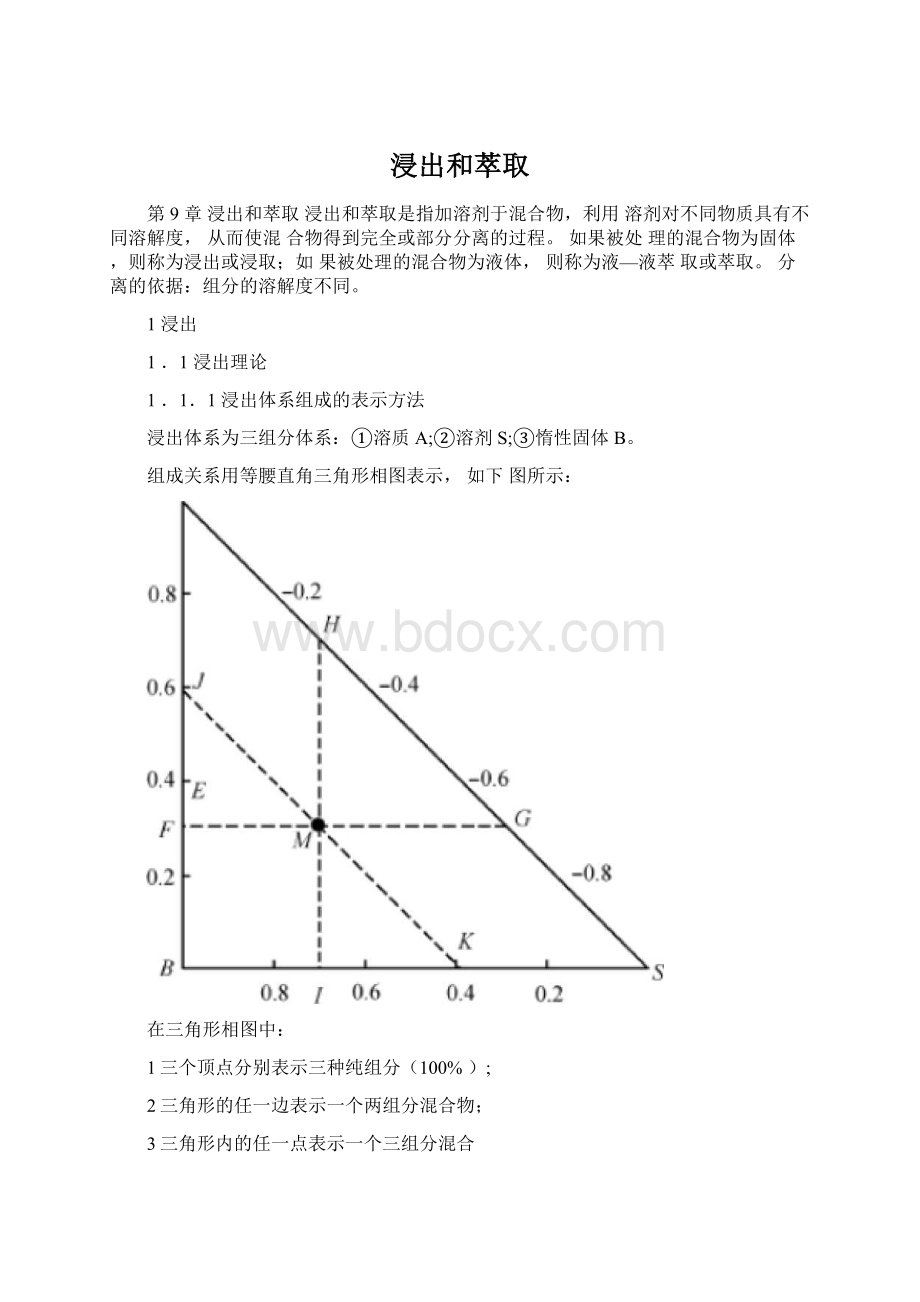
组成关系用等腰直角三角形相图表示,如下图所示:
在三角形相图中:
1三个顶点分别表示三种纯组分(100%);
2三角形的任一边表示一个两组分混合物;
3三角形内的任一点表示一个三组分混合
物;
4平行于任意一边的直线表示其所对顶角
组分的一个恒定组成,如图中的JK直线上
的任一点均表示B组分的组成为40%。
按以上规定,得图中M点的组成为:
xa=0.30;xb=0.40;xs=0.30
1.1.2浸出系统的平衡关系
浸出平衡:
固体空隙中溶液的浓度等于固体周围溶液的浓度。
理论级:
能够达到浸出平衡的浸出级(器)。
1.1.3溢流与底流平衡关系的表达
溢流:
浸出完成后,从浸出器顶部排出的均
相溶液(清液);
组成:
A+S。
底流:
从浸出器底部排出的残渣;
组成:
B+A+S。
在三角形相图上,溢流的组成点位于AS边上(图中E点);底流的组成位于BE联线上
(图中R点)。
下列符号的意义:
yA(或y)-溢流中溶质A的组成;
XA(或x)-底流中溶质A的组成
1.1.4杠杆规则
表达组成与该点质量的关系。
对BME线段:
RRM
EME
(M为支点)
MRM
ERE
(R为支点)
MME
RRE
(E为支点)
对FMS线段:
1.1.5单级浸出过程的表示
一定量的原料F(含A,B)与一定量的纯溶剂S混合,物系点M位于SF连线上;其位置由S/F决定;浸出平衡后,得溢流E和底流R。
基本物料关系:
F+S=M=R+E
平衡关系:
RRMEME
上两式联立可解得R,E。
1.2浸出速率
浸出过程由以下3个步骤组成:
1溶剂进入固体内,溶解溶质A;
2溶解的溶质从固体内部扩散到固体表面;
3溶质从固体表面扩散到外部溶液主体。
浸出速率U:
单位时间、单位浸出表面浸出的溶质质量,即
dW
Ad
亠般,U可用下式表示:
dW
Ad
式中:
A-固液接触面积,m2;
x-溶液主体内溶质的浓度;
Xa-固体表层溶质的浓度(溶质的溶解度)
K-质量传送系数。
对间歇式浸出装置,浸出液的总体积V为定值,故有下列关系式:
dW=Vdx
詈K(XaX)
dxKAZ、或丁V(Xax)
积分上式
dx
KA
xoXaX
得:
亠般,物料经过破碎或切片后表面积增加,浸出速率增大。
但应注意,物料如果过度破碎,往往会阻碍溶剂在罐内的流动,并导致一些杂质成分流入溶液中,反而造成分离困难。
1.3浸出操作的流程
三种基本流程如下:
(1)简单接触法
为间歇式浸出操作。
基本过程为:
混合、浸出T分离得溢流和底流
如图(a)所示。
(2)错流多级接触法数组简单接触法浸出装置依序排列,原料从头贯穿至尾,而每级分别有溶剂的进出。
如图(b)所示。
(3)逆流多级接触法逆流多级接触法是将数个浸出装置串联,原料和溶剂均是从头贯穿至尾,但流动方向相反。
如图(c)所示。
(4)连续微分逆流接触法连续微分逆流触法是指在浸出装置内,物料与溶剂互成逆向连续接触的浸出操作。
1.4浸出操作计算
计算项目:
①浸出所需的时间;②浸出器的大小;③溶剂用量;④浸出级数。
1浸出所需的时间决定于浸出的速率。
2浸出器的大小,通常也凭经验确定
一般,V料=75〜80%V器。
3溶剂的用量由物料衡算式求出。
4浸出器的级数由操作条件和分离要求确
浸出效率:
浸出所需的理论级数N与实际级
数Nr之比,即:
n=N/Nr
浸出级数的求取有代数计算方法和图解法两种。
(1)浸出级数的代数计算法
适用条件:
恒底流。
恒底流:
从每一个浸出器底部排出的底流量均相同。
在如图所示的N级逆流系统中:
F-原料流量,kg/h;
L-底流中的溶液量kg/h;
S-溶剂流量kg/h;
V-溢流量kg/h,V=S
第i级的溶质衡算式为:
Vyi+Lxi=Vyi+i+Lxi-i
理论级,则xi=yi(不计惰性固体)令a=V/L,则上式变为:
xi-i=(a+1)xi-axi+i
对第2级:
xi=(a+1)x2-ax3=
或
对第1级,E^V,对全系统进行物料衡算,
总物料:
F+V=L+E+B
(2)
溶质:
FxF+Vys=Eye+Lxn
(3)
将
(1)代入(3),并注意到
yE=x1,整理
可得:
a1
a1
a1
若ys=O(新鲜溶剂),则
(4)
Ea1a
L,
N-理论级数
[例9-1:
某甜菜制糖厂,以水为溶剂每小时处理100t甜菜片。
甜菜含糖12%,水48%,甜菜渣40%,出口溶液含糖15%。
设浸出系统为多级逆流接触浸出,每一个浸出器内溶液与甜菜片有充分时间达到平衡,而且每吨甜菜渣含溶液3t。
今拟回收甜菜
片中含糖的97%,若级效率为70%,问此系统需要几个浸出器?
解:
A=100X0.12=12t/h
B=100X0.40=40t/h
E迅®耳9777.6t/h
ye0.15
L=BK=40X3=120t/h总物料衡算:
100+S=77.6+120+40
S=V=137.6t/h
a=V/L=137.6/120=1.15ai=E/L=77.6/120=0.647
新鲜溶剂,ys=0。
代入(4)式
11aN
1a1-
R1a
得:
解得:
N=15.3实际级数:
Nr=N/n=15.3/0.7=21.9=22
实际浸出级数为22个。
⑵浸出级数的三角形相图法
适用条件:
恒底流与非恒底流。
以三级逆流浸出操作流程为例,如图所示:
图中符号S,V,E,F的意义同代数计算法,但底流以总量为计算基准,即:
Ln=W。
溢流中不含惰性固体,为两组分溶液
(A+S),底流为三组分混合物(B+A±^)各级的组成标于图中。
底流中惰性固体量的关系:
FXFB=L1X1B=L2X2B=L3X3B
设对底流Li而言,单位质量惰性固体所持有
的溶液量为Ki,则第i级的底流组成为:
恒底流时,K1=K2=K3=K
非恒底流时,Ki为变数
底流曲线为一条曲线mn。
若已知Ki,yiA,则可画出一条曲线
由各级的物料衡算得如下关系:
第1级:
F+V2=E+L1
(a)
E-F=V2-L1
第2级:
Ll+V3=V2+L2
二V2-Li=V3-L2(b)
由此得:
E-F=V2-Li=V3-L2=S-W=△=常数
按杠杆规则,在相图上△代表线段EF、V2Li、
V3L2和SW的共同外分点,此点称为差点
(操作点)。
图中线段ViLi代表第i个理论级。
图解法求浸出级数的步骤:
1)建立等腰直角三角相图,并绘出底流曲
线;
1
C1恒底流时,按xB值作一条平行于斜边的直线mn
C2非恒底流时,由给出的Ki,yiA按下式求
XiA,XiS:
XiA
込x(1yiAK
Ki1,XiSKi1
描出一条曲线mn2)确定△点由XFA,yEA,XS定出F,E,S三点,联EF
得一线段EF,
xfar
C1恒底流时,有XwAxfb(K1),按此值在
AB边上定出一点,并作水平线与底流线相交,得交点W,联SW得一线段SW,线段
EF与SW延长线的交点即为△点
C2非恒底流时,有
据此比例,可在AB边上定出C点,则EF与
SC联线的延长线的交点即为△点。
(SC联线与底流线mn的交点为W点)
3)联BE在底流曲线mn上得交点Li,再联
△Li在斜边上得交点V2,之后再联BV2,在底流线mn上得交点L2,……,如此下去,直到BVn联线过W点或低于W点为止。
过B点的线段数目(不包括两直角边)就是所求
1.5浸出装置
(1)单级浸出罐
为间歇式操作方式。
如图所示:
洗水入口
1
新帑剖一
Xu
(2)连续移动床浸出器
连续式浸出操作是原料和溶剂同时作连续的逆流流动。
食品生产中常见的浸出装置有:
①斗式渗滤浸出机如图所示:
落剂
X干料细片
o、
湿料细丿卜
CD
CD
o
CD
CD
CD
2萃取
几个名词:
萃取剂S:
萃取操作加入的溶剂;
溶质A:
被萃取的物质;
稀释剂(原溶剂)B:
原料液中的溶剂;
萃取相E:
萃取后分出的富含萃取剂的一相;
萃余相R:
萃取后剩余的原料液;
萃取液E0:
萃取相除去萃取剂后的溶液;
萃余液R0:
萃余相除去萃取剂后的溶液。
对萃取剂的基本要求:
与稀释剂完全不互溶或部分互溶。
萃取操作过程如下:
①混合f②澄清-③回收溶剂。
2.1液一液相平衡关系
萃取体系为3组分体系:
A+B+S
组成表示:
三角形相图。
以部分互溶体系情况(最常见)为例讨论
(1)溶解度曲线和联结线
溶解度曲线:
在一定温度下,组分的溶解度
萃取操作必须位于两相区内
共轭相:
互成平衡的两个液相(图中R和E);
联结线(平衡线):
联结共轭相的线段(线段RE);
⑵辅助曲线和临界混溶点
辅助曲线:
用于关联平衡关系的曲线。
作用:
求取平衡关系(联结线)。
临界混溶点:
辅助曲线与溶解度曲线的交点。
意义:
联结线的长度无限短(或两共轭相的溶液浓度无限接近)。
量与组成的关系可用杠杆规则描述,如F与
S的混合点为M(和点),萃取平衡后分成
共轭相E和R(差点)
应用杠杆规则,有:
FFMSSM
EEMRRM
物料关系:
F+S=M=E+R
(3)分配系数和选择性系数
分配系数:
在一定温度下,组分在共轭相E
与R中的浓度之比,即:
kbk也
kAkB
Xa,Xb
式中:
yA,yB-分别为组分A,B在萃取相E
中的质量分数;
xa,XB-分别为组分A,B在萃余相R中的质
量分数。
kA值越大,萃取分离的效果愈好。
一般,kA=f(T)。
选择性系数B:
溶质(A)的分配系数与稀释
剂(B)的分配系数之比,即:
kAYa/Xa
kByB/Xb
萃取操作中,要求B>1。
(4)温度对相平衡关系的影响
通常,Tf,互溶度T,两相区面积J。
22萃取过程的计算
在以下计算中,所有的萃取级均假定为理论
级。
定义:
萃取率nA为萃取到萃取相中的溶质质
量与原料中的溶质质量之比,即:
显然,AA1
2.2.1单级萃取的计算
F+Sf混合(ME+Rf脱溶剂fE°+R°
在三角形相图上的表示如下:
当M点已知时,需用试差作图法(借助辅助曲线)求过M点的联线ER。
基本物料关系:
F+S=M=E+R
及E°+R°=F
杠杆规则:
FMF=SMS
EME=RMR
ERE=MMR
E0E0F=ROR°F
E0max的求法:
从S点作溶解度曲线的切线,与AB边的交点即E0max。
2.2.2多级错流萃取
多级错流萃取在三角形相图上的图解实为
单级萃取图解的多次重复,方法如下:
1由Si/F的比值定出Mi点;
2过Mi试差作图得Ei和Ri(过Mi的联结
线);
Ei+R1=Mi=F+S1
RiRiEi=MiMiEi
上两式联立可求得Ri,(Ei)o
3由S2/Ri的比值定出M2点;
4过M2试差作图得E2和R2(过M2的联结线);
E2+R2=M2=Ri+S2
R2R2E2=M2M2E2
上两式联立可求得R2,(E2)
如此反复,直到Rn,(Xn,达到或低于Rn
(Xn)(Xn已知)为止。
所作联结线的个数即为所需的理论级数。
总溶剂用量St:
St=S1+S2++Sn
当Si=S2==Sn=S,St最小。
对于完全不互溶体系,
若分配曲线为Y=KX,
且各级的溶剂用量相等
S,则理论级数N为:
Ln(1Am)XnYs/K
式中:
Am=KS/B
2.2.3多级逆流萃取
如图所示:
订:
《心
2
A
J
溶剂
原料
I-
一申睪余相
:
险&扣脣
J
R
(b)
线
级间物料关系:
F-Ei=Ri-E2==Rn-S=△
图解法求级数的步骤:
①在三角相图上绘出溶解度曲线和辅助曲
②由S/F的比值定出M点;
③联Rn(Xn),M得El;
溶解度曲纯
、E\辅肋曲线局
联结线
④联Ei,F得线段EiF,联S,Rn得线段
SRn,线段EiF与sRn延长线的交点即为
△;
⑤过Ei作联结线得Ri,联△,Ri得E2,
过E2作联结线得R2,联△,R2得E3,……,如此反复,直到Rn,(Xn,)达到或低于Rn
(Xn)为止。
所作联结线的个数即为所需的理论级数。
关于最小溶剂用量Smin的问题:
当溶剂用量小至Smin时,达到指定的分离要求需要的理论级数为无穷多。
在三角相图上表现为某一条操作线与联结
线重合。
对于完全不互溶体系,若分配曲线为Y=KX,则理论级数N为:
式中:
Am=KS/B
[例9-3]在多级逆流萃取装置中,用纯
溶剂S处理含溶质A为30%的原料液。
已知原料液处理量为2000kg/h,溶剂用量为700kg/h,要求最终萃余相中溶质A的质量分数不超过7%。
试求:
①所需的理论级数;②若将最终萃取相中的溶剂全部脱除,求最终萃取液的流量和组成。
操作条件下的溶解度曲线和辅助曲线如本题附图所示解:
(1)所需的理论级数
①由xf=30%在AB边上定出F点,联结
FS。
操作溶剂比为S/F=700/2000=0.35
2由溶剂比在FS线上定出和点M。
3由Xn=7%在相图上定出Rn点,联结RnM并延长交溶解度曲线于E1点,此点即为最终萃取相组成点。
4作点Ei与F、点S与Rn的联线,并延长两线交于点4。
5过点Ei作联结线Ei及Ri,联结点4,Ri
并延长交溶解度曲线于E2点,……重复上述步骤,当作至联结线E5R5时,x5
=5%<7%,即为5个理论级。
(2)最终萃取液的流量和组成联接点S、Ei
并延长交AB边于点Ei0,此点即代表最终
萃取液的组成点。
由图读得yi°=0.87。
辅助豹线
8
-6
应用杠杆规则求Ei0的流量:
E1RnE1MMRn
即:
43E1(2000700)19.5
・・・Ei=1224kg/h
即:
91.5E「122443.5
・・・E1°=582kg/h
2.3萃取操作的设备
1)混合澄清槽
萃取剂
萃取相
萃余相
2)筛板塔
3)往复筛板塔
B
脉动待板
轩相
璽液进口
轻液出口
轻液进口
量液出口
两相界而
币利
4)离心萃取器