非饱和土力学作业.docx
《非饱和土力学作业.docx》由会员分享,可在线阅读,更多相关《非饱和土力学作业.docx(14页珍藏版)》请在冰豆网上搜索。
非饱和土力学作业
《非饱和土力学课程作业》
*******
*******
学号:
********
日期:
2012/6/25
非饱和土力学土坝渗流稳定分析
问题描述:
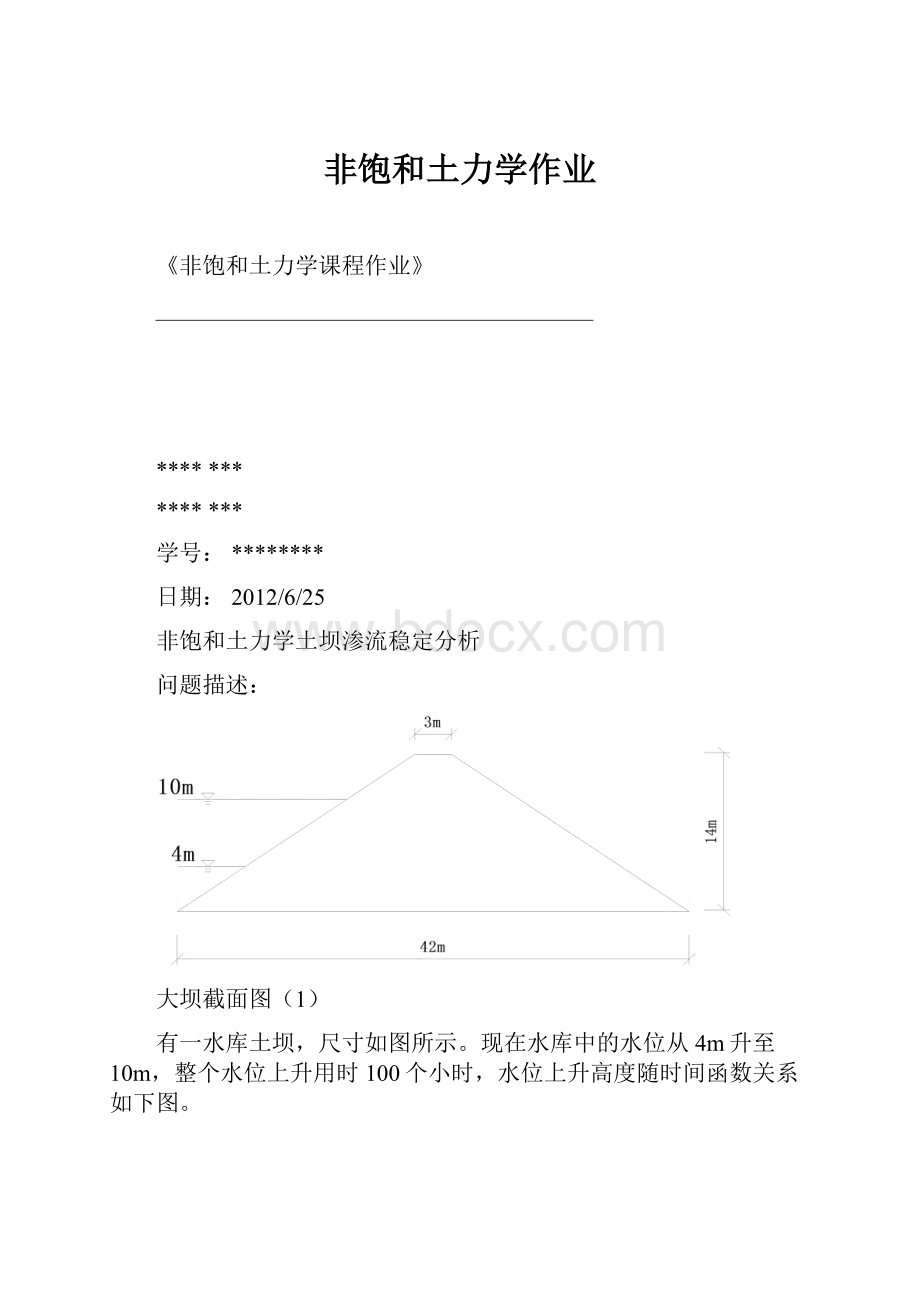
大坝截面图
(1)
有一水库土坝,尺寸如图所示。
现在水库中的水位从4m升至10m,整个水位上升用时100个小时,水位上升高度随时间函数关系如下图。
图
(2)大坝水位上升时间曲线
大坝土吸力-体积含水量,吸力-渗透系数曲线如下图所示:
图(3)吸力-渗透系数曲线
图(4)吸力-体积含水量图
大坝土的力学参数指标如下表所示:
表1、大坝土物理参数指标
重度(kN/m3)
粘聚力(Kpa)
内摩擦角(°)
17
20
20
试分析当水位由4m升至10m时,土坝中浸润面的变化情况,以及该土坝的稳定性?
问题求解
一、渗流分析求解:
1、4m初始水位稳态分析
(1)建模、网格划分及材料性质输入:
图1.1.1最终建模结果
图1.1.2吸力—渗透系数关系图1.1.3吸力—体积含水量关系
依据题述模型尺寸建立如上模型,其中材料土水特性如上图所示,网格为四边形—三角形混合形式,大小为1m。
模型边界条件为左端红色线总水头4m,右边蓝色线边界条件为总流量0m3/s,右端底坡脚点边界条件为总水头0m,其余边界条件为软件默认不透水边界。
(2)模型计算结果:
图1.1.4四米水位稳态分析
2、水位由4米升至10m瞬态分析:
(1)模型设置:
改变上述稳态模型的边界条件,按题述,设置左边红色边界为水位-时间函数关系,水位在前100小时按线性升高,100小时至19656小时,水位维持在10m,水位函数如下图所示:
图1.2.1水位随时间上升函数
(2)模型计算结果:
图1.2.20小时浸润面位置
图1.2.350小时浸润面情况
图1.2.4100小时浸润面情况
图1.2.5200小时浸润面情况
图1.2.6300小时浸润面情况
图1.2.71000小时浸润面情况
图1.2.82000小时浸润面情况
图1.2.95000小时浸润面情况
图1.2.1019656小时后浸润面情况
(3)计算分析
从上述浸润面计算结果可以看出,浸润面随水位升高不断变化,当100小时后水面达到稳定的10m,此时浸润面仍未达到稳定,根据计算结果分析,大约在1000小时左右,浸润面才达到稳定。
二、稳定分析
1、水位4米时土坝稳定分析:
稳定分析的模型轮廓与渗流分析相同,土坝选用摩尔—库伦模型,模型所需参数如下表所示:
重度(kN/m3)
粘聚力(Kpa)
内摩擦角(°)
17
20
20
土坝稳定分析时的孔压为上稳态渗流分析结果。
计算结果:
(1)Mogenstern-Price法计算最优滑裂面结果:
(2)普通条分法计算结果:
(3)Bishop法计算结果
(4)Jian-bu法计算结果:
四种计算方法算的最优滑裂面的安全系数如下表所示:
计算方法
Mogenstern-Price法
普通条分法
Bishop法
Jian-bu法
最小安全系数
1.463
1.404
1.461
1.390
从上述计算可知,四种计算方法最小安全系数在1.390—1.463之间,平均安全系数为1.430,可知在水位上升前土坝处于稳定状态。
2、水位升高后土坝稳定分析
稳定分析的模型轮廓与上述渗流分析相同,土坝选用摩尔—库伦模型,模型所需参数如下表所示:
重度(kN/m3)
粘聚力(Kpa)
内摩擦角(°)
17
20
20
土坝稳定分析时的孔压为上次瞬态分析19656小时计算结果。
计算结果:
(1)Mogenstern-Price法计算最优滑裂面结果:
显示50条安全系数最小的滑裂面图:
(2)普通条分法计算结果:
显示50条安全系数最小的滑裂面图:
(3)Bishop法计算结果
显示50条安全系数最小的滑裂面图:
(4)Jian-bu法计算结果:
显示50条安全系数最小的滑裂面图:
(5)其他相关参数计算结果:
最优滑移体从上至下空隙水压力分布:
最优滑移体从上至下抗剪强度分布:
2、计算结果分析:
四种计算方法算的最优滑裂面的安全系数如下表所示:
计算方法
Mogenstern-Price法
普通条分法
Bishop法
Jian-bu法
最小安全系数
1.237
1.187
1.257
1.273
四种计算方法最小安全系数范围为1.187—1.257,平均值为1.239,说明在水位升高过程中以及其后过程,土坝是稳定的。
比较水位上升前其平均安全系数降低了0.192
从上述沿边坡从上至下孔压分布可以看出,在距离边坡顶部约9m的地方孔压开始为正,其后孔压随距离先增大在减小至零,大约在距离边坡顶部20m处孔压达到最大值42Kpa。
从上述沿边坡从上至下抗剪强度分布可以看出,在孔压由负变为正的点,抗剪强度有一个峰值,此外在孔压最大点,抗剪强度也有一个峰值,且此峰值大于孔压由负变正点。