数值分析作业第一次Word下载.docx
《数值分析作业第一次Word下载.docx》由会员分享,可在线阅读,更多相关《数值分析作业第一次Word下载.docx(34页珍藏版)》请在冰豆网上搜索。
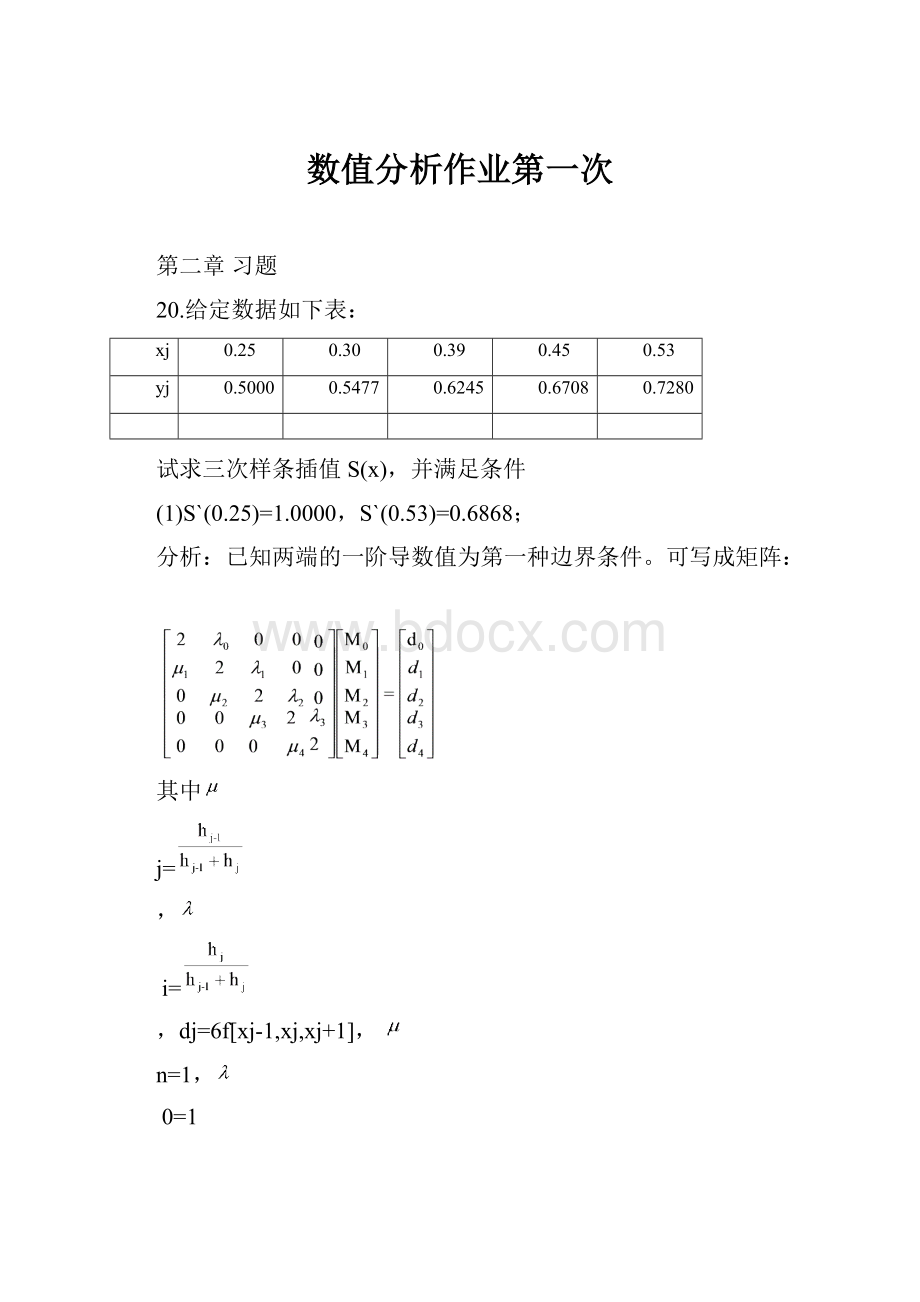
0.6000
0.6429
-3.2667
0.0600
0.4286
0.4000
-2.4286
0.0800
0.5714
-2.1150
、
由此得矩阵形式的线性方程组为:
解得M0=-2.0286;
M1=-1.4627;
M2=-1.0333;
M3=-0.8058;
M4=-0.6543
S(x)=
matlab源程序
>
x=[0.250.300.390.450.53];
y=[0.50.54770.62450.67080.7280];
S0=1;
S5=0.6868;
forj=1:
1:
4
h(j)=x(j+1)-x(j);
end
forj=2:
r(j)=h(j)/(h(j-1)+h(j));
r
(1)=1;
forj=1:
3
u(j)=h(j)/(h(j)+h(j+1));
u(4)=1;
f(j)=(y(j+1)-y(j))/h(j);
d
(1)=6*(f
(1)-S0)/h
(1);
d(5)=6*(S5-f(4))/h(4);
d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));
a=zeros(5,5);
fori=1:
5
a(i,i)=2;
a(i+1,i)=u(i);
a(i,i+1)=r(i);
b=inv(a);
M=b*d'
;
s=csape(x,y,'
complete'
[10.6868])
fnplt(s,'
r'
)
xlabel('
x'
ylabel('
y'
title('
三次样条插值函数'
plot(x,y,'
o'
x,y,'
'
s.coefs
(2)S``(0.25)=S``(0.53)=0.
已知两端的二阶导数只为零,可以利用自然边界条件。
,dj=6f[xj-1,xj,xj+1],
n=
0=0d0=dn=0
0.0000
-4.3147
解得M0=0;
M1=-1.8925;
M2=-0.8234;
M3=-1.2108;
M4=0.6054;
S(x)=
matlab程序:
y=[0.50.54770.62450.67080.7280];
end
r(j)=h
(1)/(h(j)+h
(1));
u(j)=1-r(j);
d(j)=6*(f
(1)-f(j))/(h
(1)+h(j));
a=zeros(4,4);
a(j,j)=2;
a(j+1,j)=u(j+1);
a(j,j+1)=r(j);
a(1,4)=u
(1);
a(4,1)=r(4);
b=inv(a);
s=csape(x,y,'
second'
[00])
title('
plot(x,y,'
第二种中情况时的s(x)函数的程序:
r
(1)=0;
d
(1)=0;
d(5)=0;
计算实习题
1已知函数在下列各点的值为
xi
0.2
0.4
0.6
.0.8
1.0
f(xi)
0.98
0.92
0.81
0.64
0.38
试用4次牛顿插值多项式P4(x)及三次样条函数S(x)(自然边界条件)对数据进行插值。
用图给出{(xi,yi),xi=0.2+0.08i,i=0,1,11,10},P4(x)及S(x)。
由差商的定义及牛顿插值多项式的表示方式可知:
f[x0,x1·
·
,xk]=
Pn=f(x0)+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+·
+f[x0,x1,·
xn](x-x0)·
(x-xn-1)
用自然边界条件。
一阶差商
二阶差商
三阶差商
四阶差商
dj
-0.3000
0.500
-3.7500
-0.5500
-0.62500
-4.5000
0.8
-0.8500
-0.75000
-0.20833
-6.7500
-1.3000
-1.12500
-0.52083
P4(x)=0.98-0.3(x-0.2)-0.625(x-0.2)(x-0.4)-0.20833(x-0.2)(x-0.4)(x-0.6)-0.52083(x-0.2)(x-0.4)(x-0.6)(x-0.8)
解得:
M0=0;
M1=-1.5165;
M2=-0.9339;
M3=-1.6228;
M4=0
程序:
四次牛顿插值程序:
x=[0.20.40.60.81.0];
fx=[0.90.920.810.640.38];
%由此函数可得差分表
n=length(x);
fprintf('
*****************差分表*****************************\n'
);
FF=ones(n,n);
FF(:
1)=fx'
fori=2:
n
forj=i:
FF(j,i)=(FF(j,i-1)-FF(j-1,i-1))/(x(j)-x(j-i+1));
fori=1:
fprintf('
%4.2f'
x(i));
i
%10.5f'
FF(i,j));
\n'
4;
x=[0.20.2811.08];
y(i)=0.98+0.1*(x(i)-0.2)-1.625*(x(i)-0.2)*(x(i)-0.4)+1.45833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-2.60417*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)*(x(i)-0.8);
b'
牛顿四次插值'
三次牛顿插值程序:
y=[0.980.920.810.640.38];
%向前提
variation'
x1=0.2;
y=-1.3393*(x1-0.4)*(x1-0.4)*(x1-0.4)-0.2464*(0.2-x1)+0.9800*(x1-0.4);
a=y;
x1=0.28;
b=y
x1=1;
y=-1.3393*(x1-0.4)*(x1-0.4)*(x1-0.4)-0.2464*(0.2-x1)+0.9800*(x1-0.4);
c=y
x1=1.08;
y=-1.3393*(x1-0.4)*(x-0.4)*(x1-0.4)-0.2464*(0.2-x1)+0.9800*(x1-0.4);
d=y
x2=[abcd]
m=[0.20.2811.08]
h=fnval(m,s)
plot(m,h,'
s.coefs
xlabel('
ylabel('
)
图1.1
3下列数据点的插值
1
9
16
25
36
49
64
2
6
7
8
可以得到平方根函数的近似,在区间[0,64]上作图。
(1)用这9各点作8次多项式插值L8(x).
(2)用三次样条(自然边界条件)程序求S(x)。
从结果看在[0,64]上,那个插值更精确;
在区间[0,1]上,两种哪个更精确?
L8(x)可由公式Ln(x)=
得出。
三次样条可以利用自然边界条件。
写成矩阵:
l0(x)=
l1(x)=
l2(x)=
l3(x)=
l4(x)=
l5(x)=
l6(x)=
l7(x)=
l8(x)=
L8(x)=l1(x)+2l2(x)+3l3(x)+4l4(x)+5l5(x)+6l6(x)+7l7(x)+8l8(x)
0.2500
-2.6250
0.3750
0.7500
-2.3542
0.4167
0.6250
-2.5243
0.4375
0.5833
-0.0084
0.4500
0.5625
-4.8037
11
0.4583
0.5500
-2.7518
48
13
0.4643
0.5417
-2.7867
15
0.5357
解得:
M0=0;
M1=-1.1200;
M2=-0.5132;
M3=-1.4523;
M4=1.0184;
M5=-2.5065;
M6=-0.4526;
M7=-1.2883;
M8=0
图3-1为[064]的曲线为拉格朗日插值函数与三次样条插值函数如图中所示。
由图3-1可以看出,绿色的线条更靠近红色的线条,三次样条插值函数的曲线更接近函数曲线,几乎是重合的;
图3-2在[01]区间,是绿色的线几乎和红色的线重合,可能是程序写的不够完美,从图上看三次样条插值的曲线接近函数曲线。
由图3.2可以看出在区间[0,1]上,S(x)更精确。
L8(x)matlab编程[064]上程序:
x1=[01491625364964];
y1=[012345678];
P=polyfit(x1,y1,8);
%8表示8次多项式
X=0:
64;
Y=polyval(P,X);
plot(x1,y1,'
r--'
X,Y,'
b-'
9点8次多项式插值'
图3-1
三次插值在区间[064]的程序:
x=[01491625364964];
y=[012345678];
u(9)=0;
d(9)=0;
a=zeros(9,9);
M=b*d'
variational'
h=fnval(s,X)
r-'
X,h,'
g*'
三次样条插值函数自然条件'
图3-1
L8(x)在区间[01]的程序:
P=polyfit(x1,y1,8);
X=0:
0.01:
1;
plot(x1,y1,'
)xlabel('
)ylabel('
三次插值在区间[01]的程序:
fnplt(s,'
0.1:
图3-2
图3-2
第三章
16.观测物体的直线运动,得出下数据
时间t/s
00.91.93.03.95.0
距离s/m
010305080110
求运动方程。
解:
根据所给数据,在坐标纸上标出,见图16-1,从图中看到各点在一条直线附近,故可选择现行函数做拟合曲线,即令y=ax+b.这里m=5,n=1,
0=1,
1=x,故
(
j,
k)=
j(xi)
k(xi),(f,
k)=
f(xi)
k==dk,k=0,1,……n,
法方程:
Ga=d,a=(a0,a1,……an)T,d=(d0,d1,……dn)T,
G=
由法方程得:
=
由matlab计算得,
=
;
,所以运动方程:
y=-15,0002x+15.9804
Matlab程序:
x=[00.91.93.03.95.0];
y=[010305080110];
+'
)%画给出的点的图,看趋于那类型的图形,为后面设方程打基础
figure
A=polyfit(x,y,1);
%拟合成二次曲线,A为返回值
%提取系数
a=A
(1);
b=A
(2);
%画原图
plot(x,y);
holdon;
%保存图
%画拟合图
plot(x,a*x+b,'
holdoff;
计算的matlab程序:
t=zeros(2,2);
5;
t(1,1)=t(1,1)+1;
5t(1,2)=t(1,2)+x(i);
end
5t(2,1)=t(2,1)+x(i);
5t(2,2)=t(2,2)+x(i)^2;
A=zeros(2,2);
A(1,1)=A(1,1)+y(i);
A(2,1)=A(2,1)+y(i)*x(i);
m=A(:
1)end
d=inv(t)
a=d*m
图16-1
由求出来的矩阵可知道拟合的方程与原方程的拟合比较得:
图16-2
18.在某化学反应中,由实验得分解物浓度与时间关系如下:
0510152025303540455055
浓度y/(*10*(-4))
01.272.162.863.443.874.154.374.514.584.624.64
用最小二乘法算求y==f(t)
根据所给数据,在坐标纸上标出,见图18-1从图中看到各点在一条直线附近,故可选择现行函数做拟合曲线,
,它不是线性形式,两边取对数得:
㏑y=㏑a-b/x;
如令Y=
㏑y,A=㏑a,则得Y=A-b/x;
={1,x}.为确定A,b,先将(xi,yi)转化为(xi,Yi).
根据最小二乘法,取
,得