职高数列知识点及例题有答案Word文件下载.docx
《职高数列知识点及例题有答案Word文件下载.docx》由会员分享,可在线阅读,更多相关《职高数列知识点及例题有答案Word文件下载.docx(9页珍藏版)》请在冰豆网上搜索。
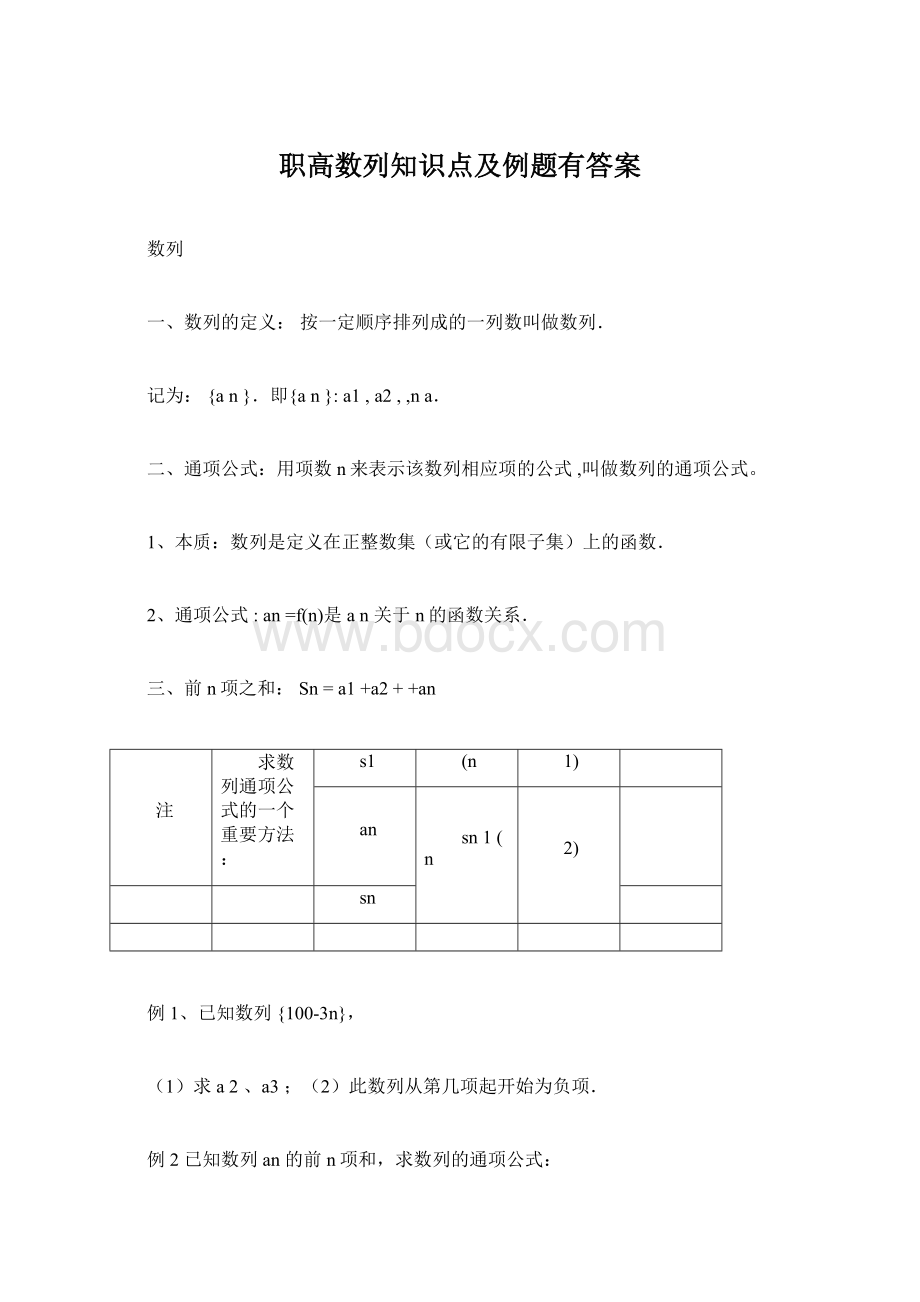
sn
例1、已知数列{100-3n},
(1)求a2、a3;
(2)此数列从第几项起开始为负项.
例2已知数列an的前n项和,求数列的通项公式:
(1)Sn=n2+2n;
(2)Sn=n2-2n-1.
解:
(1)①当n≥2时,an=Sn-Sn1=(n2+2n)-[(n-1)2+2(n-1)]=2n+1;
②当n=1时,a1=S1=12+2×
1=3;
③经检验,当n=1时,2n+1=2×
1+1=3,∴an=2n+1为所求.
(2)①当n≥2时,an=Sn-Sn1=(n2-2n-1)-[(n-1)2+2(n-1)-1]=2n-3;
②
当n=1时,
a1=S1=12
×
1
-2-1=-2;
③
经检验,当n=1时,2n-3=2×
1-3=-1≠-2,∴an=
2(n
为所求.
2n
3(n
注:
数列前n项的和Sn和通项an是数列中两个重要的量,在运用它们的关
系式anSnSn1时,一定要注意条件n2,求通项时一定要验证a1是否
适合
例3当数列{100-2n}前n项之和最大时,求n的值.
分析:
前n项之和最大转化为
an0
an10.
等差数列
1.如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,
那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常
用字母d表示.即:
an1and(常数)(nN?
)
2.
ana1
(n1)d,推广:
anam(nm)d.
通项:
n(a1
an)
n(n1)
3.求和:
Sn
na1
d.(关于n的没有常数项的二次函数).
2
4.中项:
若a、b、c等差数列,则b为a与c的等差中项:
2b=a+c
5.等差数列的判定方法
(1)定义法:
an1
d(常数)(nN?
(2)中项法:
2an1an
(3)通项法:
an
a1(n
1)d
(4)前n项和法:
Sn
An2
Bn
练习:
已知数列{an}满足:
a1=2,an=an1+3,求通项an.
例1在等差数列an中,已知a49,a96,Sn63,求n.
解:
设首项为a1,公差为d,
9
a1
3d
18
3
则
得
63Sn
(
1)得:
n
6或
7
6
8d
d
18nnn
例2
(1)设{an}是递增等差数列,它的前3项之和为12,前3项之积为48,求这个数列的首项.
分析2:
三个数成等差数列可设这三个数为:
a-d,a,a+d
拓展:
(1)若n+m=2p,则an+am=2ap.
推广:
从等差数列中抽取等距离的项组成的数列是一个等差数列。
如:
a1,a4,a7,a10,(下标成等差数列)
(2)等和性:
amanapaq(m,n,p,qN*,mnpq)
(3)Sn,S2nSn,S3nS2n,组成公差为n2d的等差数列.
(4)an=am+(n-m)d
例1
(1)已知a3+a11=20,求a7.
(2)已知a3+a4+a5+a6+a7=450,求a2+a8及前9项和S9.
解由等差中项公式:
a3+a7=2a5,a4+a6=2a5
由条件a3+a4+a5+a6+a7=450,得:
5a5=450,∴a2+a8=2a5=180.
S9=
9(a1a9)810
等比数列
1.定义与定义式:
从第二项起,每一项与它前一项的比等于同一个常数的
数列称作等比数列.
an1
q(q为不等于零的常数)
.通项公式:
a1qn1,推广形式:
amqnm.
na1(q
.前n项和:
a1(1
qn)
anq
0且q1)
q
(q
注:
应用前n项和公式时,一定要区分q1与q1的两种不同情况,必要的时候要分类讨论.
4.等比中项:
如果在a与b之间插入一个数G,使a,G,b成等比数列,
那么G叫做a与b的等比中项.即G2ab(Gac).
5.等比数列的判定方法:
0),则数列an是等比数列.
①定义法:
对于数列
an,若an
q(q
②等比中项:
an,若anan2
an2
1,则数列an是等比数列.
例1等比数列中a1=2,a3=8,求通项公式;
a3a1qq24q2an
(2)2n12n或an
(2)
(2)n1
(2)n
例2在等比数列{an}中,S4=1,S8=3,则a17+a18+a19+a20.
解解方程组可得:
q4=2,1a1q1,
解法2由Sn,S2n-Sn,S3n-S2n,成等比数列计算.
在等比数列an中有如下性质:
(1)若n+m=2p,则anam=(ap)2。
从等比数列中抽取等距离的项组成的数列是一个等比数列。
a1,a4,a7,a10,(下标成等差数列)
(2)等积性:
amanapaq(mnpq,m,n,p,qN).
(3
)an=amqnm
例1
在等比数列{an}中,a1
a6
33,a3a432,an1
an,
(1)求an;
(2)若Tnlga1
lga2
Llgan,求Tn.
解
(1)an26n
(2)Tn
(1n2
11n)lg2
例2a1a2a37,a1a2a38,求an.
设{an}的公比为q,由题意知
a1qa1q
7,
1,
4,
n1
n3
a1qa1q2
8,解得q
2或q
1.∴an2
或an
(2)
数列综合运用
例1公差不为零的等差数列的第二、三、六项成等比数列,求公比q.
设等差数列的通项an=a1+(n-1)d(d≠.0)
根据题意得
a32
26
=aa
即(a+2d)=(a+d)(a+5d),
a3
2d
1d
解得a1
所以q
3.
d.
a2
例2有四个数,其中前三个数成等差数列,后三个数成等比数列,且第
一个数与第四个数的和是16,第二个数与第三个书的和是12,求这四个数.
a
(ad)
设这四个数为:
ad,a,ad,(a
d)
16
,则
2a
12
解得:
4
或
,所以所求的四个数为:
4,4,12,36;
或15,9,3,1.
8