第四单元《三位数乘两位数》Word文档格式.docx
《第四单元《三位数乘两位数》Word文档格式.docx》由会员分享,可在线阅读,更多相关《第四单元《三位数乘两位数》Word文档格式.docx(18页珍藏版)》请在冰豆网上搜索。
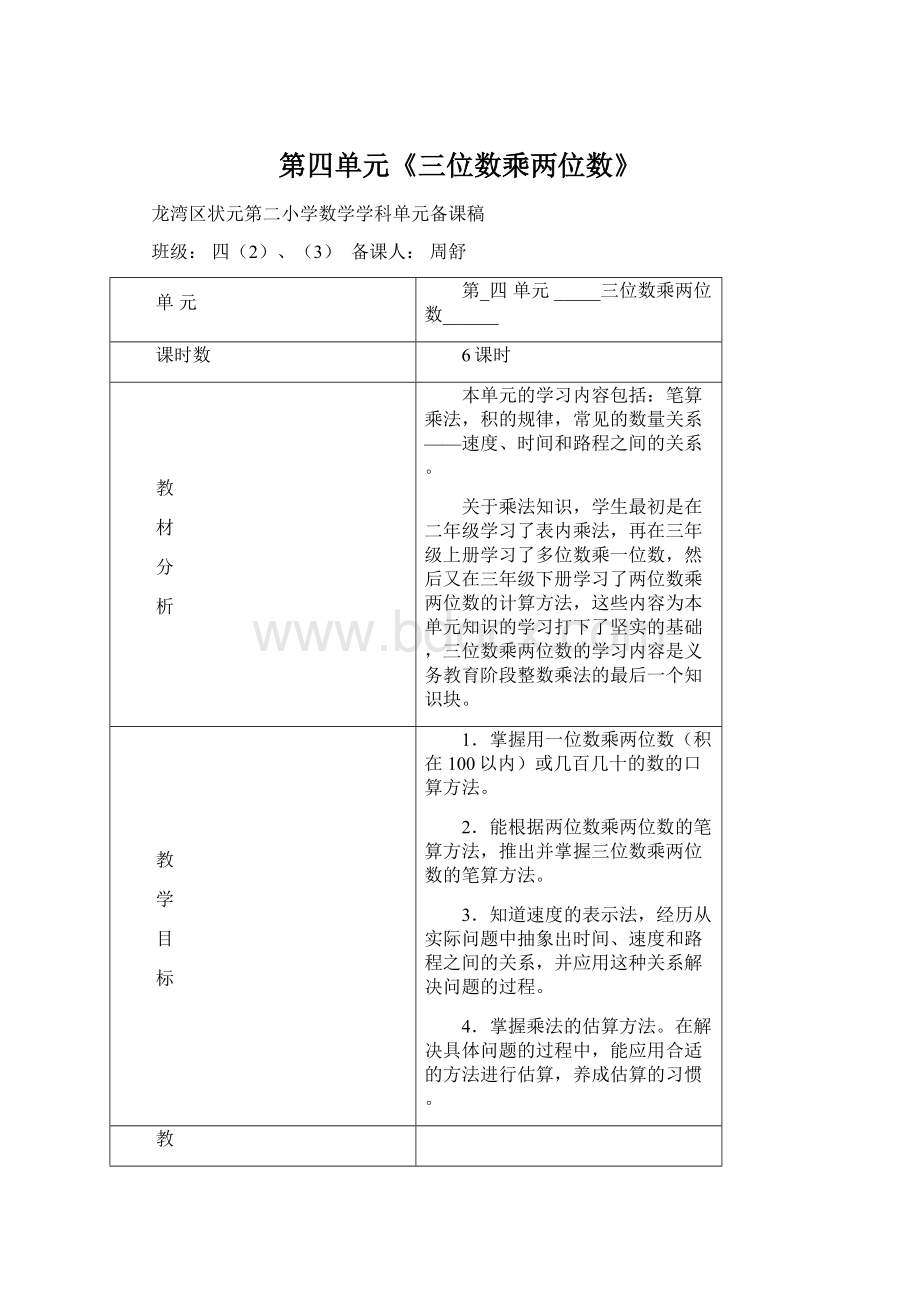
59=63×
52=
这节课我们在此基础上继续学习笔算乘法
二、探索发现
1、出示例1:
李叔叔从某城市乘火车去北京用了12小时,火车1小时约行145千米。
该城市到北京大约有多少千米?
问:
说一说这题如何列式?
这是一道什么样的乘法算式?
(板书教学内容补充:
三位数乘两位数)
145×
12估计一下大约是多少?
(指名回答)
怎么计算出准确的结果?
能不能用我们以前学过的旧知识来解决这道题,自己试一试。
(小组讨论并汇报)
提问:
(1)先算什么?
(先算2乘145的积是290,得数的末位和因数的个位对齐)
随笔
(2)再算什么?
积的书写位置怎样?
(3)最后算什么?
注意第二步个位上的0不写。
板书:
12=1740
145
×
12
290
145
1740
和45×
12比较,你发现了什么相同点?
小结:
两位数乘法笔算的方法是什么?
师生归纳
两位数乘法,先用一个因数个位上的数去乘另一个乘数,得数的末尾和个位对齐;
再用这个因数十位上的数去乘另一个乘数,得数的末尾和十位对齐,最后把两次乘得的积加起来。
三、巩固练习
1.P47做一做
134×
12176×
47425×
36237×
82
322×
24145×
27679×
13286×
35
2、练习七的第5题。
(1)认真读题,弄清题意。
(2)分几步解答,先算什么,再算什么。
(3)学生独立解答,并进行检验。
(4)反馈解答情况。
3、练习七第2题
怎么算出5天有多少分钟?
学生独立完成后,让学生根据知识背景说说自己的感受。
四、总结
说一说你有什么收获。
随笔
五、作业设计:
1.列竖式计算下面各题
113×
26=125×
12=423×
16=
2.解决问题
(1)学校组织秋游活动,全校有学生324人,每人费用25元。
一共需要多少元?
(2)小明每天在上跑步15分钟,他的速度大约是每分钟跑145米,小明每天早上跑步多少米?
板书设计
三位数乘两位数笔算
145×
12=1740(千米)
×
——————
290
———————
课后反思
因数中间、末尾有0的乘法
1、掌握因数末尾有0的竖式的简便写法及计算方法
2、口算、笔算交互进行,培养学生自主解决问题的能力
3、运用乘法计算解决问题。
4、培养细心、严谨的解题态度。
掌握因数中间或末尾有0的计算方法。
掌握竖式的简便写法。
末尾或中间有0时,竖式有没有简便写法?
一、复习导入
1.口算
40×
72=600×
300=30×
23=
53×
30=20×
700=40×
22=
72=40×
72=
20×
20=40×
90=502×
7=
608×
5=908×
4=400×
50=
2.笔算并说一说笔算的方法是什么?
708×
6=790×
8=54×
278=
这节课继续学习笔算乘法板书教学内容:
二、创设情境
1、出示例2
怎样计算160×
30=
能不能用我们以前学过的旧知识来解决,自己试一试。
学生独立进行计算。
(1)请不同算法的学生说一说口算的过程。
总结:
可以用口算计算先算160×
3=480,再在积的末尾再添1个0;
或16×
3=48,再在积的末尾添写2个0
(2)写竖式时,如何处理0和非0数字的对位问题?
怎样确定积的末尾0的个数?
(指名板演,其他学生在本上完成。
)
2、学生根据题意,独立写出解题算式,独立进行计算
反馈第
(1)题:
请不同算法的学生说一说
重点围绕竖式的简便写法和积进行讨论
①写竖式时,如何处理“0”和“非0”数字的对位问题
②怎样确定积的末尾零的个数
反馈第
(2)题:
重点围绕竖式的简便写法
160×
30=4800
30
—————
4800
106
——————
3180
三、质疑与小结
1、因数末尾有0如何列竖式简便?
应注意什么?
两个因数末尾都有0的简便算法是“先把0前面的数相乘,再看两个因数末尾一共有几个0,则在积的末尾添写几个0。
2、因数中间有0,计算时应注意什么?
乘数中间有0的乘法,用0乘这一步可以省略。
但要注意用乘数哪一位上的数乘,乘得的数的末位就要和那一位对齐。
四、知识反馈
1、学生试练教材P53做一做
2、比较哪个算式简便,为什么?
360360
25×
25
五、巩固练习
1、练习八第1、2题
2、学生独立完成,全班讨论订正
小组讨论交流计算的过程
用自己的话说一说计算的过程。
使学生通过自主探索,掌握因数中间或末尾有0的计算方法
六、课堂总结
今天你都学会了什么?
有什么收获?
七、作业
课堂作业:
《课堂作业本》P20.
课外作业:
练习八第3、4、7题
被乘数中间或尾末数有0的乘法
特快列车每小时可行160千米,普通列车每小时可行106千米。
它们30小时各行多少千米?
30=4800(千米)106×
30=3180(千米)
160
三位数乘两位数的笔算练习
练习课
1.巩固三位数乘两位数的笔算的方法。
2.培养计算能力,形成计算的技能。
3.经历巩固笔算乘法计算的全过程,进一步巩固算理和计算的方法
4.培养认真计算的良好学习习惯。
5.感受所学知识的应用价值,增强应用意识。
巩固三位数乘两位数的计算方法
能正确、熟练地计算
说说口算的方法是什么?
笔算乘法的方法是什么?
一、复习导入;
1、口算
28×
3=16×
8=36×
2=
46×
20=4×
160=3×
150=
150×
6=26×
7=20×
19=
200×
73=900×
24=430×
8=
每组一行,生独立口算,汇报:
2、笔算
24=27×
145=679×
13=
笔算乘法的计算方法是什么?
板书课题:
笔算乘法练习
二、练习内容:
(一)判断并改错。
134152246
16×
23×
34
---——————————
804156964
134104638
————————————
93811967344
说一说找到的错处和纠正的结果、错的原因和怎样避免。
笔算时应注意什么?
(二)解决问题
1、观赏蔬菜
导语:
同学们,张叔叔种植了品种繁多的观赏蔬菜,他邀请我们去他家做客,去欣赏一下他心爱的宝贝。
请看课本第51页第8题。
(1)让学生说说:
你知道了什么数学信息?
(2)这道题给出什么条件,求什么?
(3)让学生说说数量关系式(单价×
数量=总价),并尝试做题。
(4)学生独立解题后,让学生汇报解题过程。
(5)四人小组里说说你还发现了什么数学问题,然后指名学生回答。
(要求学生提出问题并列式。
2、图书馆购书
导语:
同学们,为了丰富大家的课外阅读,学校将为图书馆增添两种新书,请看课本第52页第9题。
(1)你知道了哪些数学信息?
谁还想说说?
这道题要我们求什么?
会不会求?
(2)学生尝试做题后,请学生来说说他的方法?
预设方法一:
125×
3=375(元)
75×
3=125(元)
375+125=600(元)
预设方法二:
125+75=200(元)
200×
3=600(元)
师:
谁来说说你是怎么想的?
每一步求出的是什么?
(3)师:
对比这两种方法,你喜欢哪一种方法?
为什么?
三、拓展延伸
生独立思考,再小组讨论汇报:
说说自己的思考过程。
?
76
————————
18?
—————————
31?
0
四、课堂总结
五、作业
《课堂作业本》P19
1、笔算
124×
73=46×
215=224×
36=
2、选择
(1)236×
12在竖式计算中,十位上的1乘236得()
A.236B.2360C.472
(2)512×
29的积最接近()
A.15000B.10000C.1500
3、练习八第12、13题。
笔算乘法?
31?
积的变化规律
1.通过观察,能够发现并总结积的变化规律。
2.经历变化规律的发现过程,感受发现数学中的规律是一件十分有趣的事情。
3.尝试用简洁的语言表达积的变化规律,培养初步的概括和表达能力。
4.初步获得探索规律的一般方法和经验,发展学生的推理能力。
5.培养初步的抽象、概括能力及善于观察、勤于思考、勇于探索的良好习惯。
自己发现并总结积的变化规律。
一个因数不变,另一个个因数不断变大(小),积的变化?
从上面的例子,你发现了什么规律?
一、研究“两数相乘,其中一个因数变化,它们的积如何变化的规律”。
1、研究问题,概括规律
(1)两数相乘,一个因数不变,另一个因数乘几时,积怎么变化。
学生完成下列两组计算,想一想发现了什么?
你能根据每组算式的特点接下去再写两道算式吗?
试试看
6×
2=8×
125=
20=24×
200=72×
组织小组交流
归纳规律:
两数相乘,当一个因数不变,另一个因数乘几时,积也要乘几。
(2)两数相乘,一个因数不变,另一个因数除以几时,积有
怎么变化?
学生完成下列两组计算,想一想有发现了什么?
80×
4=25×
160=
40=
10=
引导学生概括:
两数相乘,当一个因数不变,另一个因数除以几时,积也要除以几。
(3)整体概括规律
谁能用一句话将发现的两条规律概括为一条?
引导学生总结规律。
2、验证规律
(1)先用积的变化规律填空,再用笔算或计算器验算。
26×
48=17×
12=
24=17×
24=
12=17×
自己举例说明积的变化规律
3、应用规律
完成例4下面的做一做和练习9的第1——4题
第1题:
汽车用同样的时间可行()千米,得先算出汽车的速度,再算4小时的路程。
第2题:
比较理解“增加到24米”与“增加了24米”的区别。
第3题:
找准六道式中相同的因数与发生变化的因数。
二、研究“两数相乘,两个因数都发生变化,积变化的规律”。
1、独立思考,发现规律
完成下列计算,说规律。
18×
(18÷
2)×
(24×
2)=
(18×
(24÷
105×
45=
(105÷
5)×
(45×
5)=(105×
3)×
(45÷
3)=
2、组织全班交流,概括规律
两数相乘,一个因数乘(或除以)几,另一个因数除以(或乘)几,它们的乘积不变。
3、你还能举几个这样的例子吗?
三、拓展巩固
一个长方形的面积是256平方厘米,如果长缩小到原来的1/4,宽扩大到原来的4倍,这个长方形就变成了正方形,这个正方形的面积是多少?
它的边长是多少?
这节课有什么收获?
还有什么疑问?
《课堂作业本》P23
课外作业
1、我能填
(1)一个因数乘10,另一个因数不变,积应()。
(2)两个因数同时除以10,积应()。
(3)一个因数乘10,另一个因数除以10,积()。
2、请根据积的变化规律填空。
42×
78=327615×
16=240
39=()60×
16=()
84×
78=()15×
320=()
3、根据320×
7=2240填空
(1)(320)×
(7×
4)=2240
(2)(320÷
8)×
(7)=2240
(1)6×
2=128×
125=1000
(2)8×
6×
20=12024×
125=300040×
200=120072×
125=900020×
两数相乘,当一个因数不变,另一个因数乘(或除以)几时,积也要乘(或除以)几。
两种常见的数量关系
1.初步认识单价、数量、总价以及速度、时间、路程的含义,在具体生活情境中理解和掌握这两组数量关系。
2.认识这些常见的数量关系中各种不同数量的求法,会应用这些常见的数量关系解决一些实际问题。
3.初步培养学生运用数学术语的能力和综合、抽象、概括的能力,渗透事物之间相互联系的观点。
初步认识单价、数量、总价以及速度、时间、路程的含义,在具体生活情境中理解和掌握这两组数量关系。
初步培养学生运用数学术语的能力和综合、抽象、概括的能力,渗透事物之间相互联系的观点。
你知道单价、数量与总价之间的关系吗?
速度,时间与路程之间的关系?
一、情境导入:
谈话:
同学们,这有一些物品的价格信息,请你来做售货员,算一算要花多少钱?
(出示教材P52例4)
二、探究新知
1.教学例4
(1)篮球每个80元,买3个要多少钱?
(2)鱼每千克10元,买4千克要多少钱?
学生尝试列式解答,指名汇报并板书。
说一说,这两道题的条件有什么共同的特点?
都是求什么的问题?
两道题都是讲的买商品的价钱问题,题中篮球每个80元、鱼每千克10元,这样的每一件商品的价钱是单价(板书:
单
价),买3个、买4千克这样买的件数是数量(板书:
数量),求一共用的钱是总价(板书:
总价)。
找一找,数学书的单价是多少?
你还知道哪些物品的单价。
每小时,每分钟都表示单位时间。
单位时间可以是每小时、每分钟、每秒、每日等等
(3)试着写出其他交通工具的速度。
学生写出自己熟悉的交通工具的速度,在班上交流。
说一说第
(1)题中篮球的单价、数量、总价各是多少,怎样求总价?
(2)题呢?
从上两题中你能发现单价、数量、总价之间的关系吗?
生概括并板书
想一想如果知道总价、数量怎样求单价呢?
生汇报
如果知道总价和单价又该怎样求数量呢?
我们在识记这一组数量关系时,只要记住“单价×
数量=总价”就可以根据乘法算式各部分之间的关系,就能想出“总价÷
数量=单价”“总价÷
单价=数量”
2.教学例5,出示例题,独立解答
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少米?
两道题都是讲的行程问题,题中每小时行70千米、每分钟行225米,这样的在一个单位时间里行的路程,是速度(板书:
速度),所用的4小时、10分钟是行走的时间(板书:
时间),求出的280千米、2250米,这样的一共行的路是路程(板书:
路程)。
说一说第
(1)题中汽车的速度、时间、路程各是多少,
怎样求路程?
从上两题中你能发现速度、时间、路程之间的关系吗?
生概括并板书。
想一想如果求速度,又该知道哪两个条件呢?
怎样列式?
生汇报如果求时间,又该知道哪两个条件呢?
我们在识记这一组数量关系时,只要记住“速度×
时间=路程”就可以根据乘法算式各部分之间的关系,就能想出“路程÷
时间=速度”“路程÷
速度=时间”
三、巩固新知
1、猎豹奔跑的速度可达每小时110千米,可写作:
2、蝴蝶的速度每分钟500米,写作:
3、声音传播的速度是每秒钟340米,写作:
4、小强每天早上跑步15分钟,他的速度大约是120米/分,小强每天大约跑步多少米?
5、练习八第8、9题
《课堂作业本》P21-22。
练习八第10题
单价×
数量=总价速度×
时间=路程
总价÷
数量=单价路程÷
时间=速度
单价=数量路程÷
速度=时间