中国石油大学《概率论及数理统计》复习计划试题及文档格式.docx
《中国石油大学《概率论及数理统计》复习计划试题及文档格式.docx》由会员分享,可在线阅读,更多相关《中国石油大学《概率论及数理统计》复习计划试题及文档格式.docx(19页珍藏版)》请在冰豆网上搜索。
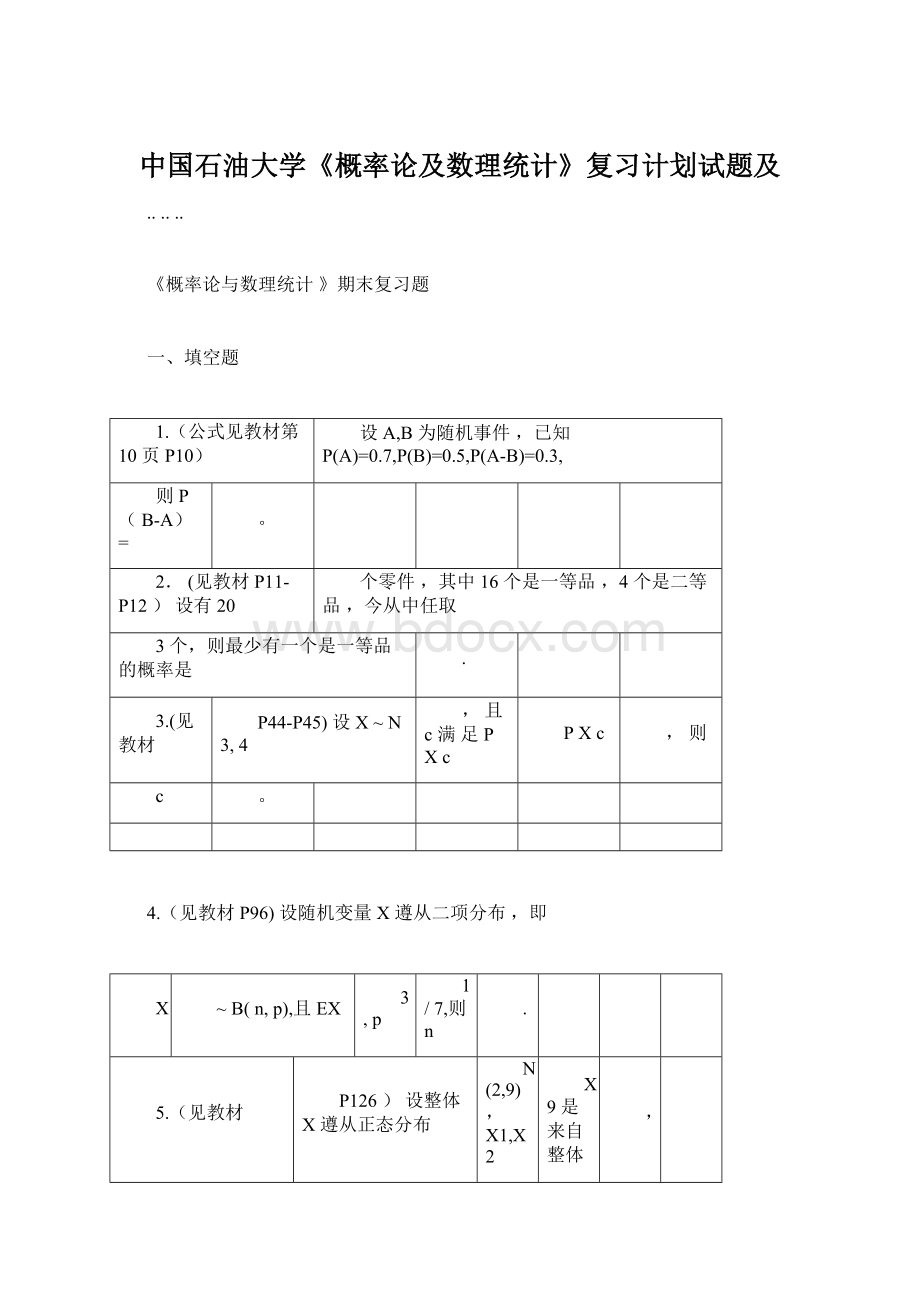
(2)
0.9772,则P{
2
6}
10.(见
教
材
P96)
设
随
机
变
量
服
从
二
项
分
布
即
X~B(n,p),且EX
1/5,则n
.专业专注.
11(见教材P42)
连续型随机变量X的概率密度为fx
e3x,
x
则
0,
.
12.(见教材P11-P12)盒中有12只晶体管,其中有10只正品,2只次品.现从盒中任取
3只,设3只中所含次品数为
X,则PX1
13.(见教材P73-P74)
已知二维随机变量(X,Y)~N(1,
2;
12,22;
),且X与Y相互
独立,则
______.
二、选择题
1.(见教材P37-38)设失散型随机变量X的分布列为
P
其分布函数为
F(x),则F(3)=
A.0
C.
D.
x,
f
x2
x,1
2.(见教材P39-40)
设随机变量X的概率密度为
其他
则X落在区间
0.4,1.2内的概率为(
).
(A)0.64;
(B)0.6;
(C)0.5;
(D)0.42.
3.(见教材P133-136)矩估计是(
)
A.点估计
B.极大似然估计
区间估计
D.无偏估计
4.(见教材P31)甲乙两人下棋,每局甲胜的概率为
,乙胜的概率为
0.6,。
比赛可采用三
局两胜制和五局三胜制,则采用时,乙获胜的可能性更大?
A.三局两胜制B.五局三胜制
C.五局三胜制和三局两胜制都相同D.无法判断
5.(见教材P69和P71和P100)以下结论正确的选项是()
A.ξ与η相互独立,则ξ与η不相关B.ξ与η不独立,则ξ与η相关
C.ξ与η不相关,则ξ与η相互独立D.ξ与η相关,则ξ与η相互独立
6(见教材P33).每次试验的成功率为p(0p1),则在3次重复试验中最少失败一次的概
率为()。
A.(1p)2B.1p2C.3(1p)D.以上都不对
7.(见教材44页)设随机变量X拥有对称的概率密度,即fxfx,又设Fx为
X的分布函数,则对任意a0,PXa().
(A)21Fa;
(B)2Fa1;
(C)2Fa;
(D)12Fa.
8.(见教材10页)对于任意两个事件A与B,必有P(A-B)=()
A)、P(A)-P(B)B)、P(A)-P(B)+P(AB)CP(A)-P(AB)DP(A)+P(B)
9.(见教材第17页)某种动物活到25岁以上的概率为,活到30岁的概率为,则现
年25岁的这种动物活到30岁以上的概率是()。
A)、B)、C)、D)、
10.(见教材第37到第39页)设F(x)和f(x)分别为某随机变量的分布函数和概率密度,则必
有()
A)、f(x)单调不减B)、F(x)dx1C)、F()0D)、
F(x)f(x)dx
11.(教材第
95到第98)随机量X与Y相互独立,且X~B16,1
,Y遵从于
参数9的泊松分布,D(X
2Y1)(
)。
A)、–14
B)、–13
C)、40
D)、41
12.(教材
91希望的性
)随机量
X的数学希望存在
,E(E(E(X)))
(
A)、0
B)、D(X)
C)、E(X)
D)、E(X)2
13.
(教材126)X1,X2,⋯,Xn来自正体N(,
)的本,本均X的
分布(
2)
A)、
N(,)
B)、N(,
C)、
N(0,1)
D)、
n
N(n,n2)
14.(教材125)体X~N(0,0.25),从体中取一个容量6
的本X1,⋯,X6,
(X1
X2)2
Y=(X3X4
X5X6)2
,若CY遵从F(1,1)分布,C(
A)、2
B)、1
C)、2
D)、1
15.(教材第7
)事件A
B
C分表示甲、乙、丙三人某合格,用ABC表
示以下事件。
A)、3人均合格;
B)、3人中最少有
1人合格;
C)、3人中恰有1人合格;
D)、3人中至多有
1人不合格;
三、(第一章18,全概率公式和叶斯公式)工厂A和工厂B的品的次品率分是
1%和2%,从由A和B的品分占60%和40%的品中随机抽取一件,
(1)抽到的这件产品为次品的概率是多少
?
(2)若是抽到的产品为次品,则该次品属于
A厂生产的概率为多少
四、(第三章,56
页二维连续随机变量
,58
页边缘分布)设随机变量(X,Y)的联合概率
密度为
f(x,y)
Axy
(X,Y)
G
其中G{(X,Y)0x
1,0
yx
}
求:
(1)求常数A;
(2)X,Y的边缘概率密度。
(3)求P(X
五、(第三章53页,失散二维随机变量和第四章
88页二维随机变量函数的数学希望
)已
知失散型随机变量
X和Y的联合分布律以下
Y
(1)概率P{X
Y};
(2)数学希望E(XY).
2/9
4/9
1/9
六、(第八章假设检验165页,单个正态整体希望的检验)设某次考试的考生成绩遵从正
态分布,从中随机地抽取36位考生的成绩,算得平均成绩为66.5分,样本标准差为15分,
问在显然性水平0.05下,可否可以认为此次考试全体考生的平均成绩为70分?
并给出检验
过程.(t(35)2.0301)。
七、(第七章参数估计133-143页点估计,两种方法)设整体X的概率分布为
3
2(1
12
其中
1)是未知参数,利用整体
的以下样本值
:
,,
(0
03
求
的矩估计值和最大似然估计值。
八、(第二章39页连续型随机变量的概率密度)已知随机变量X的分布密度函数为
Ax,0x2
(x)
0,其他
(1)常数A;
(2)概率P1
;
九、(第三章第三节独立性
68页,第三章第五节77
页卷积公式)设X和Y是
两个相互独立的随机变量,其概率密度分别为:
x1
e
y
fX(x)
,fY(y
(1)(X,Y)的联合概率密度函数;
(2)
Z
Y的概率密度。
十、(见材P11-P12
)设X1,X2,
Xn是取自整体X的一个样本,整体
X~f(x)
ex,x
,(
0)。
试求:
未知参数
的矩估计量
的最大似然估计量
L。
《概率论与数理统计》期末复习题参照答案
一、填空答案
1.
2.284/285
5.1/2
8.-2/3
11.
.12.
9/2213.
_0__.
二、答案
三、B:
“任意抽取一件,抽到次品”。
A1:
“任取一件品,抽到的是A厂生的”
A2:
“任取一件品,抽到的是B厂生的”
P(A1)0.6,P(A2)0.4,P(B|A1)0.01,P(B|A2)
P(B)
P(Ai)P(B|Ai
i
P(A1|B)
P(A1)P(B|A1)
3/7
四、
f(x,y)dxdy1
即0dx0Axydy1
A
12
(2)当0
x1时,fX(x)
f(x,y)dy
12xydy6x5
⋯⋯
6x
0x1
fX(x)
⋯⋯..⋯⋯⋯
当0
y1时,fy(y)
y12xydx6y6y2
6y
6y2
0y1
fY(y)
(3)
P(X
)12
dx0xydy
63
64
五、
(1)p(XY)0
(2)解法一:
XY分布列以下:
XY
-1
-2
3/9
所以:
E(XY)=
4
10
解法二:
E(XY)
六、解:
次考的学生成
X,
则X~N(,
2),
..
..
样本均值为:
X,样本标准差
S
提出假设:
H0:
70,
H1:
70
由于
未知,故采用
t
检验法
当H0为真时,统计量拒绝域:
70~t(n1),
S/
t/2(n1)
由于n
36,
66.5,S
15,
t(35)
2.0301,
获取:
所以接受tH0,认为全体考生的平均成绩是70
分2。
.0301,
15/
36
七、E(X)
(1
3(1
(31303123)2
8
令:
EX
x,即:
34
2得?
对于给定的样本值,似然函数为:
L(
6(1
)2(1
2)4
lnL()ln46ln
2ln(1
)4ln(12)
dlnL()6
628
24
d
)(1
解
得
713
不合题意,所以
?
1,2
因
MLE
八、解:
(1)由
1得A
(x)dx1,则Axdx
(2)P{1
21
2}
xdx
九、(20分)解:
(1)f(x,y)
fX(x)fY(y)
ey
0x
1,y
z
z0
1ez
(2)fZ(z)
fX(x)fY(zx)dx
exzdx0z1
0z1.
exzdx1z
(e1)1z
十、(20分)
(1)
矩估计量
X,
E(X)
(2)
最大似然估计量