最新浙教版八年级上册数学动点题及答案解析优秀名师资料.docx
《最新浙教版八年级上册数学动点题及答案解析优秀名师资料.docx》由会员分享,可在线阅读,更多相关《最新浙教版八年级上册数学动点题及答案解析优秀名师资料.docx(21页珍藏版)》请在冰豆网上搜索。
最新浙教版八年级上册数学动点题及答案解析优秀名师资料
浙教版八年级上册数学动点题及答案解析
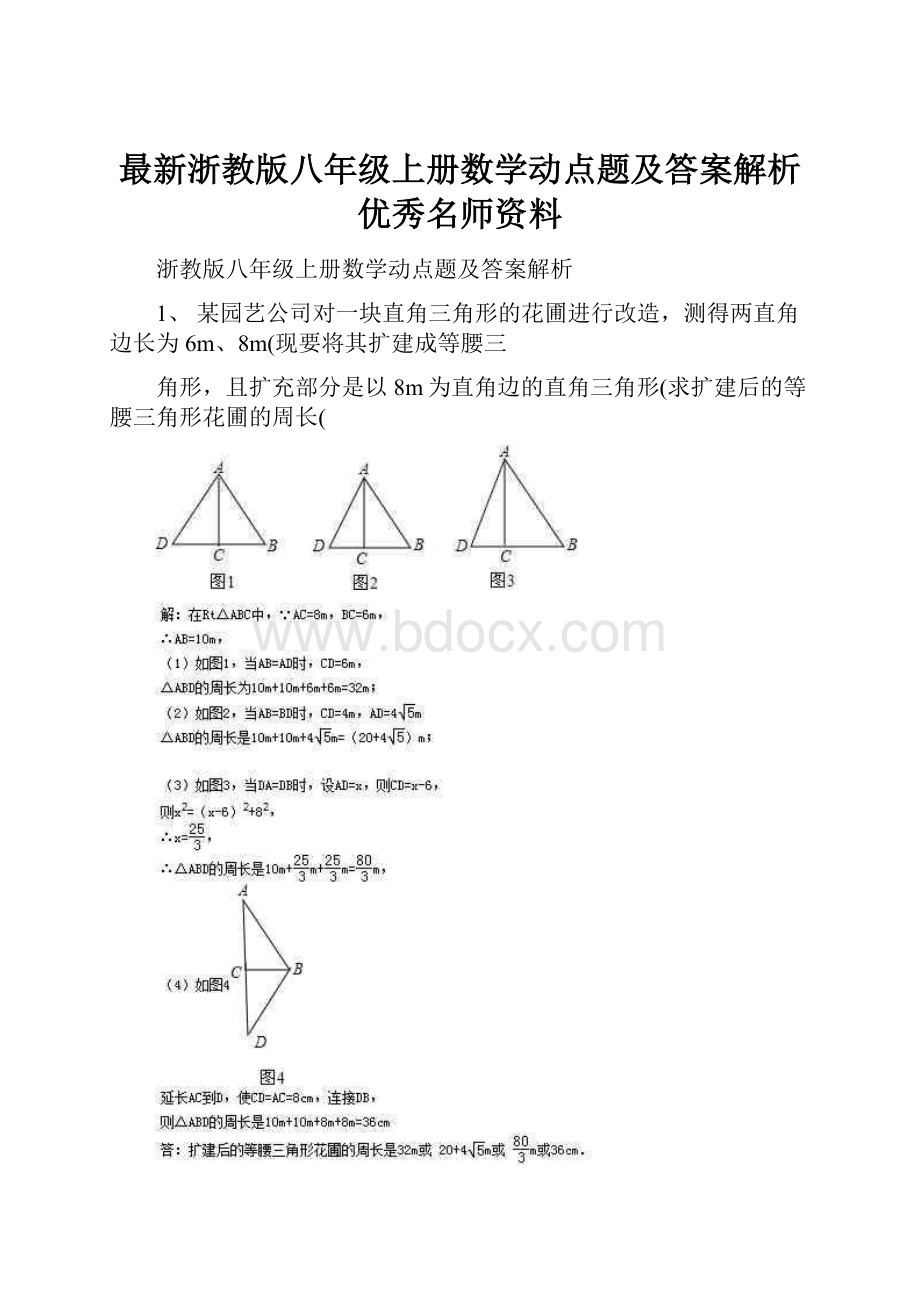
1、某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m、8m(现要将其扩建成等腰三
角形,且扩充部分是以8m为直角边的直角三角形(求扩建后的等腰三角形花圃的周长(
2、已知直线m的解析式为与x轴、y轴分别交于A、B两点,以线
段AB为直角边在第一象限内作等腰Rt?
ABC,?
BAC=90?
,在坐标平面内
有一点P(a,2),且?
ABP的面积与?
ABC的面积相等(
(1)求A,B两点的坐标;
(2)求?
ABC的面积;
(3)求a的值(
3、如图,已知?
ABC中,?
ABC=90?
,AB=BC,三角形的顶点在相互平行的三条直线l、l、l上,且相123
邻两平行线之间的距离均为1,则AC的长是()
4、在平面直角坐标系中,点A在第一象限,点B在第二象限,点C在坐标轴上,满足三角形ABC是Rt三角形
的点C最多有a个,最少有b个,则a+b的值为
解:
1、AB为斜边。
以AB为直径做圆,则C点为圆与坐标轴的交点。
最多有4个,最少有2个。
。
2、AB为直角边。
分别过A和B点做线段AB的垂线。
则与坐标轴最多有4个交点,最少有两个(AB与X轴平行)
综合上述,a=8,b=4。
因此a+b=12。
。
6、如图,直线y=-3/4x+6与x轴、y轴的交点分别为A、B两点,点Q是线段OA的中点,点P从点O
出发,以每秒1个单位的速度沿O?
B?
A方向运动,运动时间为t秒,当点P到达A时,运动停止。
(1)点A、B的坐标分别为___________、____________;
(2)在点P的运动过程中,求满足S?
OPQ=1/3S?
OBA的点P的坐标;
(3)在点P的运动过程中,是否存在点P,使?
OPQ是等腰三角形,若存在,请求出t的值;
若不存在,请说明理由。
7、如图,在平面直角坐标系中,当三角板直角顶点P的坐标
为(3,3)时,设一直角边与x轴的正半轴交于点A,另一直角边与Y轴交于点B,在三角板绕丶P
旋转的过程中,使得?
POA为等腰三角形。
请写出所有
满足条件的点B坐标____________________.
解:
?
POE是等腰三角形的条件是:
OP、PE、EO其中两段
相等,P(3,3),那么有:
?
PE?
OC和F点过(0,0)点,PE=OE,
则F点是(0,3)和(0,0);
?
P坐标为(3,3),
?
OP=3根号2
?
PE?
OP和F点过(0,6-3根号2),
则PE=OP,
则F点是(0,6+3根号2)和(0,6-3根号2)(,,如图
(1),?
ABC中,AB=AC,?
B=2?
A(
(1)求?
A和?
B的度数;
(2)如图
(2),BD是?
ABC中?
ABC的平分线:
?
写出图中与BD相等的线段,并说明理由;直线BC上是否存在其它的点P,使?
BDP为等腰三角形,如果存在,请在图(3)中画出满足条件的?
所有的点P,并直接写出相应的?
BDP的度数;如果不存在,请说明理由(
解:
(1)?
AB=AC,?
B=2?
A
?
AB=AC,?
C=?
B=2?
A
又?
?
C+?
B+?
A=180?
?
5?
A=180?
,?
A=36?
?
?
B=72?
;
(2)?
?
BD是?
ABC中?
ABC的平分线?
?
ABD=?
CBD=36?
?
?
BDC=72?
?
BD=AD=BC;
?
当BD是腰时,以B为圆心,以BD为半径画弧,交直线BC于点P(点C除外)1
此时?
BDP=1/2?
DBC=18?
(
以D为圆心,以BD为半径画弧,交直线BC于点P(点C除外)3此时?
BDP=108?
(
当BD是底时,则作BD的垂直平分线和BC的交点即是点P的一个位置(2
此时?
BDP=?
PBD=36?
11、若直线y=kx+b是由直线y=2x-6沿射线y=x(x?
0)方向平移个单位长度得到,则k和b的值分别为()
本题考查图形的平移变换和函数解析式之间的关系,在平面直角坐标系中,图形的平移与图形上某点的平移相同(平移中点的变化规律是:
横坐标左移加,右移减;纵坐标上移加,下移减(解:
?
沿y=x(x?
0)方向平移个单位长度,
?
新函数是在原函数的基础上向下平移2个单位,并向左平移两个单位,
?
得到的直线所对应的函数解析式是y=2(x+2)-6-2=2x-4(
12、如图,直线与x轴、y轴分别交于点A、B,以AB为
直角边在第一象限内作等腰Rt?
ABC,?
BAC=90?
,若点P(1,a)
为坐标系中的一个动点(
(1)求Rt?
ABC的面积;
(2)说明不论a取任何实
数,?
BOP的面积都是一
个常数;
(3)要使得?
ABC和?
ABP的面积相等,求实数a
的值(
13(阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义(下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:
设一次函数y=kx+b(k?
0)的图象为直线l,一次函数y=kx+b111122(k?
0)的图象为直线l,若k=k,且b?
b,我们就称直线l与直2212121线l互相平行(解答下面的问题:
2
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线l的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线m:
y=kx+t(t,0)与直线l平行且交x轴于点C,求出?
ABC的面积S关于t的函数表达式(
解:
设直线l的函数表达式为y=kx+b,
?
直线l与直线y=-2x-1平行,?
k=-2,
?
直线l过点(1,4),
?
-2+b=4,
?
b=6(
?
直线l的函数表达式为y=-2x+6(
直线l的图象如图(
(2)?
直线l分别与y轴、x轴交于点A、B,
?
点A、B的坐标分别为(0,6)、(3,0)(
?
l?
m,
?
直线m为y=-2x+t(令y=0,解得x=t/2,
?
C点的坐标为(t/2,0)(
?
t,0,?
t/2,0(
?
C点在x轴的正半轴上(
当C点在B点的左侧时,S=12×(3-t/2)×6=9-3t2;当C点在B点的右侧时,S=12×(t/2-3)×6=3t2-9(?
?
ABC的面积S关于t的函数表达式为S={9-3t/2(0,t,6)3t/2-9(t,6)(
14.如图,在?
ABC中,已知
AB=AC,?
BAC=90?
,BC=6cm,
直线CM?
BC,动点D从点C
开始沿射线CB方向以每秒2厘
米的速度运动,动点E也同时从
点C开始在直线CM上以每秒1
厘米的速度运动,连接AD、AE,
设运动时间为t秒(
(1)求AB的长;
2
(2)当t为多少时,?
ABD的面积为6cm,
(3)当t为多少时,?
ABD?
?
ACE,并简要说明理由((可在备用图中画出具体图形)
解:
(1)?
在?
ABC中,已知AB=AC,?
BAC=90?
所以可知AB:
AC:
BC=1:
1:
根号2
所以AB=BC/根号二=3倍根号二
(2)过A作AN?
BC,易证AN=1/2BC=3(三线合一,斜边中线定理)?
CD=2T,BC=6,?
BD=6-2t
所以1/2(6-2t)×3=6
t=1
(3)?
CM?
BC,在?
ABC中,已知AB=AC,?
BAC=90?
所以?
ABD=?
ACM=45?
因为?
ABD全等?
ACE,AB=AC
所以BD=CE,即6-2T=T
所以T=2时,?
ABD全等?
ACE。
15、如图?
,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形
OABC(
(1)求点A、C的坐标;
(2)将?
ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图?
);
(4)在坐标平面内,是否存在点P(除点B外),使得?
APC与?
ABC全等,若存在,请求出所有符合
条件的点P的坐标;若不存在,请说明理由(
(1)y=-2x+4,代入y=0得x=2,?
A(2,0)代入x=0得y=4,?
C(0,4)
(2)设D(2,y),根据折叠的性质可得CD=AD=y,BD=4-y,2?
+(4
-y)?
=y?
,解得y=2.5
设直线CD的解析式为y=kx+4,代入x=2,y=2.5得k=-0.75?
直线CD的解析式为y=-0.75x+4(3)?
点O符合要求,P1(0,0)
?
点O关于AC的对称点也是符合要求的P点,有?
ACP=?
BAC=?
ACO,?
P可在直线CD上,设P(x,-0.75x+4),(x-2)?
+(-0.75x+4)?
=2?
解得x=3.2?
P2(3.2,1.6)
?
点B关于AC的对称点也是符合要求的P点,作PQ?
y轴于点Q根据对称性得CP=CB=2,PQ=BD=1.5,CQ=2.5,OQ=1.5?
Q(0,1.5),可求得直线AP的解析式为y=-0.75x+1.5,设P(2-4/3y,y),(4-y)?
+(2-4/3y)?
=2?
,y=2.4,P3(-1.2,2.4)
16、如图,在等腰三角形ABC中,底边BC=8cm,腰长为5cm,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系(
(1)直接写出点A,B,C的坐标(
(2)一动点P以0.25cm/s的速度沿底边从点B向点C运动
(P点不运动到C点),设点P运动的时间为t(单位:
s)(
?
写出?
APC的面积S关于t的函数解析式,并写出自变量t
的取值范围(
?
当t为何值时,?
APB为等腰三角形,并写出此时点P的坐
标(
?
当t为何值时PA与一腰垂直,
17、已知:
三角形ABC中,?
A=90?
,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:
?
DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,?
DEF是否仍为等腰
直角三角形,证明你的结论
(1)连接ad
?
ABC,?
ACD,?
ABD都是等腰直角三角形,
?
?
CAD=?
BAD,AF=BE,AD=BD
?
?
ADF?
?
BDE
?
DE=DF,
且?
EDF=?
EDA+?
ADF=?
EDA+?
EDB=90?
?
?
DEF是等腰直角三角形
2)如图,照样连接AD
与1类似证得?
ADF?
?
BDE,?
?
DEF是等腰直角三角形
418、如图,在平面直角坐标系中,直线y=x+8交坐标轴于A、3
B两点,AE平分?
BAO交y轴于E,点C为直线y=x上在第一象限内一点(
求:
(1)求AB的长;
(2)点E的坐标,并求出直线AE的解析式;
42(3)若将直线AE沿射线OC方向平移个单位,请直接写出平移后的直线解析式(
19、如图?
,将两块全等的直角三角形纸板摆放在坐标系中,已知BC=4,AC=5(
(1)求点A坐标和直线AC的解析式;
(2)折三角形纸板ABC,使边AB落在边AC上,设折痕交BC边于点E(图?
),求点E坐标;(3)将三角形纸板ABC沿AC边翻折,翻折后记为?
AMC,设MC与AD交于点N,请在图?
中画出图形,并求出点N坐标(
21、已知:
如图,在直角梯形COAB中,OC?
AB,以O为原点建立平面直角坐标系,A,B,C三点的坐标分别是A(8,0),B(8,10),C(0,4),点D(4,7)是CB的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OAB的路线移动,移动的时间是秒t,设?
OPD的面积是S(
(1)求直线BC的解析式;
(2)请求出S与t的函数关系式,并指出自变量t的取值范围;
(3)求S的最大值;
(4)当9?
t,12时,求S的范围(
(3)三角形的外心的性质:
三角形外心到三顶点的距离相等.22、如图,一次函数y=-3/4x+3的图象与x轴和y轴分别交于点A和B,再将?
AOB沿直线CD对折,使点A与点B重合、直线CD与x轴交于点C,与AB交于点D(
(1)点A的坐标为(4,0)
,点B的坐标为(0,3)
第一章直角三角形边的关系;
一年级下册数学教学工作计划
(2)求OC的长度;
(3)在x轴上有一点P,且?
PAB是等腰三角形,不需计算过程,直接写出点P的坐标(
1、20以内退位减法。
23、如图,在平面直角坐标系中,A点的坐标为(4,0),点P是直线y=-1/2x+4在第一象限上的一点,
O是原点(
(1)设P点的坐标为(x,y),?
OPA的面积为S,试求S关于x的函数关系式,并直接写出自变量x
⑦圆心角:
顶点在圆心的角叫做圆心角.的取值范围;
156.4—6.10总复习4P84-90
(2)是否存在点P,使PO=PA,若存在,请求出P点的坐标;若不存在,请说明理由(
(2)三角形的外心:
三角形外接圆的圆心叫做这个三角形的外心.
三、教学内容及教材分析:
24、如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0)(
(1)请求出直线l的函数解析式;
(三)实践活动
(2)点P在x轴上,且ABP是等腰三角形,请直接写出所有符合条件的点P的坐标;(3)点C为直线AB上一个动点,是否存在使点C到x轴的距离为1.5,若存在,求出点C的坐标;若不存在,请说明理由(
6.方向角:
指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。
如图4,OA、OB、OC、OD的方向角分别是;北偏东30°,南偏东45°(东南方向)、南偏西为60°,北偏西60°。