陕西六年中考数学第25题解析.doc
《陕西六年中考数学第25题解析.doc》由会员分享,可在线阅读,更多相关《陕西六年中考数学第25题解析.doc(11页珍藏版)》请在冰豆网上搜索。
25题解析
一、例题赏析
(2013)25.(本题满分12分)
问题探究
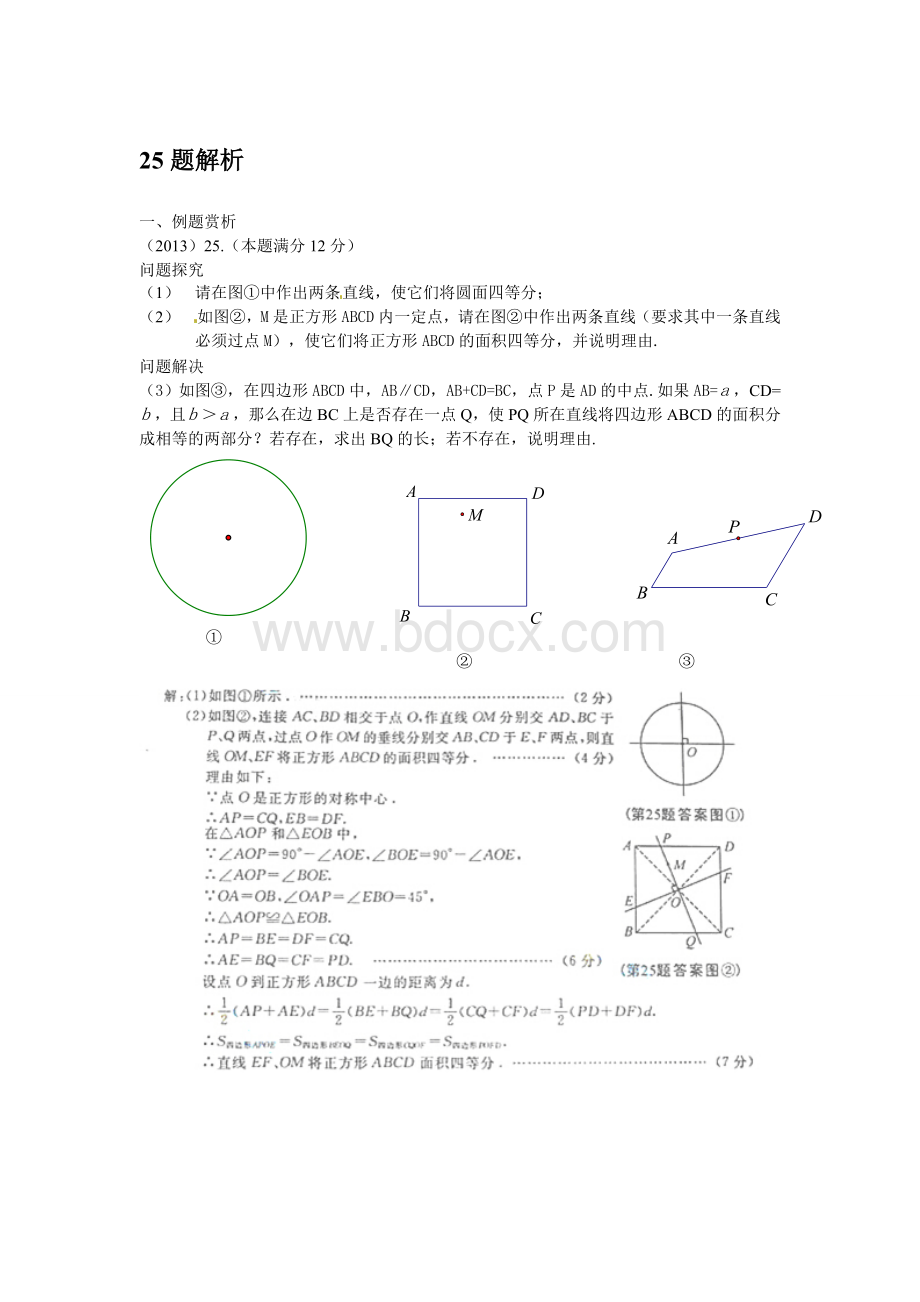
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点.如果AB=,CD=,且>,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?
若存在,求出BQ的长;若不存在,说明理由.
①
③
②
25.(2012陕西省12分)如图,正三角形ABC的边长为.
(1)如图①,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上.在正三角形ABC及其内部,以A为位似中心,作正方形EFPN的位似正方形,且使正方形的面积最大(不要求写作法);
(2)求
(1)中作出的正方形的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得D、EF在边AB上,点P、N分别在边CB、CA上,求这两个正方形面积和的最大值及最小值,并说明理由.
【答案】解:
(1)如图①,正方形即为所求。
(2)设正方形的边长为x.
∵△ABC为正三角形,∴。
∴。
∴,即。
(3)如图②,连接NE,EP,PN,则。
设正方形DEMN和正方形EFPH的边长分别为m、n(m≥n),
它们的面积和为S,则,。
∴.
∴。
延长PH交ND于点G,则PG⊥ND。
在中,。
∵,即.
∴。
∴①当时,即时,S最小。
∴。
②当最大时,S最大,即当m最大且n最小时,S最大。
∵,由
(2)知,。
∴。
∴。
【考点】位似变换,等边三角形的判定和性质,勾股定理,正方形的性质。
【分析】
(1)利用位似图形的性质,作出正方形EFPN的位似正方形E′F′P′N′,如答图①所示。
(2)根据正三角形、正方形、直角三角形相关线段之间的关系,利用等式E′F′+AE′+BF′=AB,列方程求得正方形E′F′P′N′的边长
(3)设正方形DEMN、正方形EFPH的边长分别为m、n(m≥n),求得面积和的表达式为:
,可见S的大小只与m、n的差有关:
①当m=n时,S取得最小值;②当m最大而n最小时,S取得最大值.m最大n最小的情形见第
(1)
(2)问。
25、(2011•陕西)如图①,在矩形ABCD中,将矩形折叠,使B落在边AD(含端点)上,落点记为E,这时折痕与边BC或者边CD(含端点)交于F,然后展开铺平,则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
(1)由“折痕三角形”的定义可知,矩形ABCD的任意一个“折痕△BEF”是一个 等腰 三角形
(2)如图②、在矩形ABCD中,AB=2,BC=4,,当它的“折痕△BEF”的顶点E位于AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标;
(3)如图③,在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?
若存在,说明理由,并求出此时点E的坐标?
若不存在,为什么?
考点:
翻折变换(折叠问题);勾股定理;矩形的性质;正方形的性质。
专题:
数形结合;分类讨论。
分析:
(1)由图形结合线段垂直平分线的性质即可解答;
(2)由折叠性质可知,折痕垂直平分BE,求出AB、AE的长,判断出四边形ABFE为正方形,求得F点坐标;
(3)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,
①当F在边CD上时,S△BEF≤S矩形ABCD,即当F与C重合时,面积最大为4;
②当F在边CD上时,过F作FH∥BC交AB于点H,交BE于K,再根据三角形的面积公式即可求解;再根据此两种情况利用勾股定理即可求出AE的长,进而求出E点坐标.
解答:
解:
(1)等腰.
(2)如图①,连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.
∵折痕垂直平分BE,AB=AE=2,
∴点A在BE的中垂线上,即折痕经过点A.
∴四边形ABFE为正方形.
∴BF=AB=2,
∴F(2,0).
(3)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,
理由如下:
①当F在边BC上时,如图②所示.
S△BEF≤S矩形ABCD,即当F与C重合时,面积最大为4.
②当F在边CD上时,如图③所示,
过F作FH∥BC交AB于点H,交BE于K.
∵S△EKF=KF•AH≤HF•AH=S矩形AHFD,
S△BKF=KF•BH≤HF•BH=S矩形BCFH,
∴S△BEF≤S矩形ABCD=4.
即当F为CD中点时,△BEF面积最大为4.
下面求面积最大时,点E的坐标.
①当F与点C重合时,如图④所示.
由折叠可知CE=CB=4,
在Rt△CDE中,ED===2.
∴AE=4﹣2.∴E(4﹣2,2).
②当F在边DC的中点时,点E与点A重合,如图⑤所示.
此时E(0,2).
综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4﹣2,2).
点评:
本题考查的是图形的翻折变换,涉及到矩形及正方形的性质,难度较大,在解答此题时要利用数形结合的思想进行分类讨论.
25.(12分)(2010•陕西)问题探究:
(1)请你在图①中做一条直线,使它将矩形ABCD分成面积相等的两部分;
(2)如图②点M是矩形ABCD内一点,请你在图②中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分.
问题解决:
(3)如图③,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,CD=BC=4开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处.为了方便驻区单位准备过点P修一条笔直的道路(路宽不计),并且是这条路所在的直线l将直角梯形OBCD分成面积相等的两部分,你认为直线l是否存在?
若存在,求出直线l的表达式;若不存在,请说明理由.
考点:
直角梯形;待定系数法求一次函数解析式;矩形的性质.2867872
专题:
综合题;压轴题.
分析:
(1)矩形的对角线把矩形分成面积相等的两部分.
(2)连接AC,BD中心点位P,过P点的直线分矩形为相等的两部分.
(3)假如存在,过点D的直线只要作DA⊥OB与点A,求出P点的坐标,设直线PH的表达式为y=kx+b,解出点H的坐标,求出斜率k和b.若k和b存在,直线就存在.
解答:
解:
(1)如图①.
(2)如图②连接AC、BD交于P则P为矩形对称中心.作直线MP,直线MP即为所求.
(3)如图③存在直线l,
过点D的直线作DA⊥OB于点A,
则点P(4,2)为矩形ABCD的对称中心,
∴过点P的直线只要平分△DOA的面积即可,
易知,在OD边上必存在点H使得PH将△DOA面积平分.
从而,直线PH平分梯形OBCD的面积,
即直线PH为所求直线l
设直线PH的表达式为y=kx+b且点P(4,2),
∴2=4k+b即b=2﹣4k,
∴y=kx+2﹣4k,
∵直线OD的表达式为y=2x,
∴,解之.
∴点H的坐标为(x=,y=)
把x=2代入直线PH的解析式y=kx+2﹣4k,得y=2﹣2k,
∴PH与线段AD的交点F(2,2﹣2k),
∴0<2﹣2k<4,
∴﹣1<k<1.
∴S△DHF=(4﹣2+2k)•(2﹣)=××2×4,
∴解之,得k=.(k=舍去)
∴b=8﹣2,
∴直线l的表达式为y=.
点评:
本题主要考查矩形的性质,前两问还是比较容易,但是最后一问比较麻烦,容易出错,
做的时候要认真.
25、(2009•陕西)问题探究
(1)在图①的半径为R的半圆O内(含弧),画出一边落在直径MN上的面积最大的正三角形,并求出这个正三角形的面积?
(2)在图②的半径为R的半圆O内(含弧),画出一边落在直径MN上的面积最大的正方形,并求出这个正方形的面积?
问题解决
(3)如图③,现有一块半径R=6的半圆形钢板,是否可以裁出一边落在MN上的面积最大的矩形?
若存在,请说明理由,并求出这个矩形的面积;若不存在,说明理由?
分析:
(1)如图①,△ACB为满足条件的面积最大的正三角形.连接OC,则OC⊥AB,根据垂径定理得到AB=2OB,然后利用含30°的直角三角形三边的关系求出OB,再利用三角形的面积公式计算即可;
(2)如图②,正方形ABCD为满足条件的面积最大的正方形.连接OA.令OB=a,则AB=2a,利用勾股定理求出边长,再利用正方形的面积公式计算即可;
(3)如图③,先作一边落在直径MN上的矩形ABCD,使点A、D在弧MN上,再作半圆O及矩形ABCD关于直径MN所在直线的对称图形,A、D的对称点分别是A′、D′.
连接A′D、OD,则A′D为⊙O的直径.在Rt△AA′D中,当OA⊥A′D时,S△AA′D的面积最大.
解答:
解:
(1)如图①,△ACB为满足条件的面积最大的正三角形.
连接OC,则OC⊥AB.
∵AB=2OB•tan30°=R,
∴S△ACB=.
(2)如图②,正方形ABCD为满足条件的面积最大的正方形.
连接OA.令OB=a,则AB=2a.
在Rt△ABO中,a2+(2a)2=R2.
即.
S正方形ABCD=(2a)2=.
(3)存在.
如图③,先作一边落在直径MN上的矩形ABCD,使点A、D在弧MN上,再作半圆O及矩形ABCD关于直径MN所在直线的对称图形,A、D的对称点分别是A′、D′.
连接A′D、OD,则A′D为⊙O的直径.
∴S正方形ABCD=AB•AD==S△AA′D.
∵在Rt△AA′D中,当OA⊥A′D时,S△AA′D的面积最大.
∴S矩形ABCD最大=.
点评:
本题考查了垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了等边三角形和正方形的性质以及勾股定理.
25、(2008本题满分12分)
某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
如图,甲、乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学。
点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的km处。
为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:
方案一:
供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
方案二:
供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
方案三:
供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值。
综上,你认为把供水站建在何处,所需铺设的管道最短?
北
东
D
30°
A
B
C
M
O
E
F
图①
乙村
D
30°
A
B
C
M