数值分析学期期末考试试题与答案AWord文件下载.docx
《数值分析学期期末考试试题与答案AWord文件下载.docx》由会员分享,可在线阅读,更多相关《数值分析学期期末考试试题与答案AWord文件下载.docx(10页珍藏版)》请在冰豆网上搜索。
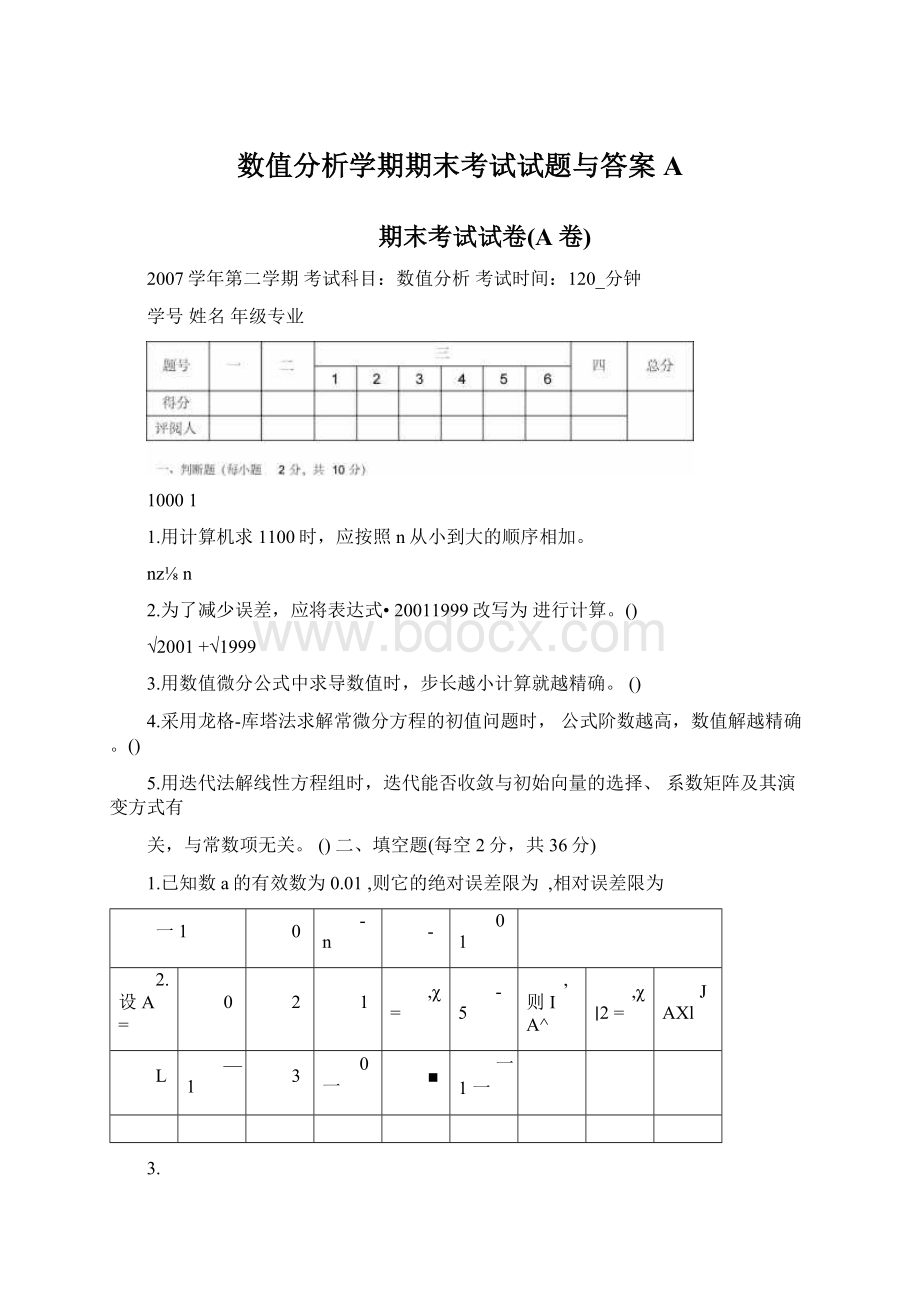
,χ=
-5
则IA^
χ∣2=
JAXl
L
—1
3
0一
■
一1一
3.
-^)A2f(0)A3f(f)的代数精度尽量高,应使
已知f(X)=2x54x3-5x,则f[-1,1,0]=,f[-3,-2,-1,1,2,3]=_.
4.为使求积公式jf(x)dxA∣f(
A=,A=,A^=,此时公式具有次的代数精度。
5.n阶方阵A的谱半径?
(A)与它的任意一种范数A的关系是.
6.用迭代法解线性方程组AX=B时,使迭代公式X(jI)=MX(Iυ∙N(k=0,1,2,∣ll)产
生的向量序列IX(k)[收敛的充分必要条件是.
7.使用消元法解线性方程组AX=B时,系数矩阵A可以分解为下三角矩阵L和上三角矩
4-21
阵U的乘积,即A=LU.若采用高斯消元法解AX=B,其中A,则
>1」
L=,U=;
若使用克劳特消元法解AX=B,则
U11二—;
若使用平方根方法解AX=B,则I11与u11的大小关系为(选填:
>,
<,=,不一定)。
V=X亠V
8.以步长为1的二阶泰勒级数法求解初值问题《'
y的数值解,其迭代公式为
IV(O)=1
三、计算题(第1〜3、6小题每题8分,第4、5小题每题7分,共46分)
1.以X0=2为初值用牛顿迭代法求方程f(X)=X-3x-1=0在区间(1,2)内的根,要求
(1)证明用牛顿法解此方程是收敛的;
(2)给出用牛顿法解此方程的迭代公式,并求出这个根(只需计算X1,X2,计算结果
取到小数点后4位)。
2.给定线性方程组
X10.4X20.4x3=1
0.4x1x20.8x3=2
0.4x10.8x2X3=3
(1)分别写出用JaCobi和GaUSS-Seidel迭代法求解上述方程组的迭代公式;
(2)试分析以上两种迭代方法的敛散性。
3.已知函数^f(X)在如下节点处的函数值
X
-1
y
4
(1)建立以上数据的差分表;
(2)根据后三个节点建立二阶牛顿后插公式PJ(X),并计算y(1.1)的近似值;
(3)采用事后估计法计算
(2)中近似值的截断误差(结果保留四位小数)。
4.已知如下数据表,试用最小二乘法求它的二次最小平方逼近多项式。
5
8
6.写出前进欧拉公式、后退欧拉公式,并由这两个公式构造一个预估-校正公式求解下列常微分方程的数值解。
*22
(0<
x<
1,h=0.2)
Jy=X+y
y(0)=0
四、(8分)已知n+1个数据点(χi,yj(i=0,1,2,IH,n),请用多种方法建立这些数据点之间的函数关系,并说明各种函数的适用条件。
期末考试答案及评分标准(A卷)
数值分析
一、判断题:
(每小题2分,共10分)
1.×
2.√3.×
4.×
5.×
二、填空题:
(每空2分,共36分)
1.0.00或0.510,0.5
2.5,'
26,15
3.0,2
4.1,0,1,3
6.T(M):
:
^101
7.
_2
8.yeyn(XnynI(IXny或yn1"
5xn2∙5yn°
.5,n"
12川三、解答题(第1〜4小题每题8分,第5、6小题每题7分,共46分)
1.
(1)证明:
f(x)=χ3-3x-1,由于
a)f
(1)=一3:
0,f
(2)=10,
b)f(x)=3x2-3=0(X(1,2)),
C)f(x)=6x0(X(1,2)),即f(X)在(1,2)上不变号,
d)对于初值X0=2,满足f
(2)f
(2)0,
所以用牛顿迭代法求解此方程是收敛的。
4分
(2)解:
牛顿迭代法的迭代公式为
取初值X。
=2进行迭代,得
Xt=1.8889,
1分
x2=1.8795.
3-0.960.256=0,即卩(一0.8)(0.40.505)(0.4—0.505)=0,
从而得∙1=-1.0928,∙2=0.8000,'
3=0.2928,(或由单调性易判断必有一个大于1
的特征根,)因此迭代矩阵的谱半径等于必大于1,所以JaCObi迭代法发散。
2分
λ0.40.4
GaUSS-SeideI迭代矩阵的特征方程为0.4乙λ0.8=0,展开得
0.4人0.8扎λ
(2-0.8320.128)=0,解得1=0,20.628,30.204,迭代矩阵的谱半径
小于1,所以GaUSS-SeideI迭代法收敛。
2分
3.解:
(1)建立差分表
△y
∆2y
A3
∆y
-4
-3
-2
2分
(2)建立牛顿后插公式为
32
P(XrQ-I(X-2)--(x-2)(X-1)
=-3(x-2)-(x-2)(x-1)
一χ24
则所求近似值为
P2(1.1)=2.79
3分
(3)根据前三个节点建立牛顿后插公式为
14
P2(I)(X)=3--(X-1)--(X-1)x
=3-(X-1)-2x(x_1)
--2XX4
则
Py(1.1)=2.68
根据事后误差估计法
R2(Xr:
1P2(0.9)-P2(I)(0.9)
故截断误差
-09
R2(1.1)(2.79-2.68):
-0.0471
3分
4268
268,MY=4
6818.6
5.解:
设F2(x)为已知节点数据的插值二次多项式。
构造如下差商表:
一阶差商
二阶差商
P2⑶
P2(3)
7
P2[3,3]
2P2[4,3,3]P2[3,3,3]
因为二次多项式的二阶差商为常数,又F2(x)是f(x)的插值函数,故有
5P2[4,3,3]=P2[3,3,3]=
P2[4,3,3]=
P2[3,3]-75
3-42
因此得
9
P2[3,3]=;
,
由于
f(k)(x)k!
Pn[χ,X,χ,∣ll,χ],
k1
从而得
f(3)=P2[3,3]=-,
f(3)=2!
P2[33,3]=5.
22
6.解:
前进欧拉公式:
yn4=yn∙h∙f(Xn,yn)=yn∙0.2Xn0.2丫“1分
后退欧拉公式:
ynynhf(Xnι,yn1)=Yn0∙2Xn10纫1
预估时采用欧拉公式
Yn1=Yn0.2Xn0.2丫.
校正时采用后退欧拉公式
2*i
Yn^yn-0.2Xn10.2头1
由初值X0=Qy0=Qh=0.2知,节点分别为X=0.2i,(i=1,2,3,4,5)
当X1-0.2,
Y1=y°
0.2X0O.2yo=0,
H0.008,
2*2
y1=y°
+0.2X1+0.2(%)
当X2=0.4,
Y2=y√0.2X10.2y10.0160,
:
0.0401.
当x3=0.6,
y3=y20.2x20.2y20.0724,
*=y20.2X30.2y3:
0.1131.
当x^0.8,
y4=y30.2x30.2y30.1877,
y4-y30.2X40.2y40.2481.
当X5=1.0,
y2=yι0.2X20.2y2
y5=y40.2x40.2y40.3884,
y5=y40.2X50.2y50.4783.
四、(8分)
答:
1、可以建立插值函数:
(1)NeWton基本差商公式
Pn(X)=f(x°
)(Xx)f[X1,X0](X-X°
)(x-%)f[X2,x1,X0]
Hl(X-X)(x-X川∣(x-XnJf[Xn,∣∣∣,X,X0]
(2)Lagrange插值多项式
Ln(X)=a。
f(x0)a1f(xjIHaif(Xi)川a.f(Xn)
(i=0,1,)l∣,n).
(x_x。
)(X-Xi4)(x-Xi1)(X-Xn)
(XiX)H∣(Xi-X4)(Xi-XJlH(Xi-Xn)
这两类插值函数的适用条件是:
n不太大;
而且要求函数严格通过已知数据点。
2、可以建立拟合函数:
Pm(XMaoaιxa2X2IIIamχm
其中系数a0,a1,a2,∣∣∣,an满足法方程组MMA=MY,
拟合函数的适用条件是:
n比较大,而且并不要求函数严格通过已知数据点,或者已知数据点本身的误差较大。