届高考一轮复习备考讲义全国用人教A版 第十四章 系列4选讲 142含答案Word文件下载.docx

届高考一轮复习备考讲义全国用人教A版 第十四章 系列4选讲 142含答案Word文件下载.docx

《届高考一轮复习备考讲义全国用人教A版 第十四章 系列4选讲 142含答案Word文件下载.docx》由会员分享，可在线阅读，更多相关《届高考一轮复习备考讲义全国用人教A版 第十四章 系列4选讲 142含答案Word文件下载.docx（19页珍藏版）》请在冰豆网上搜索。

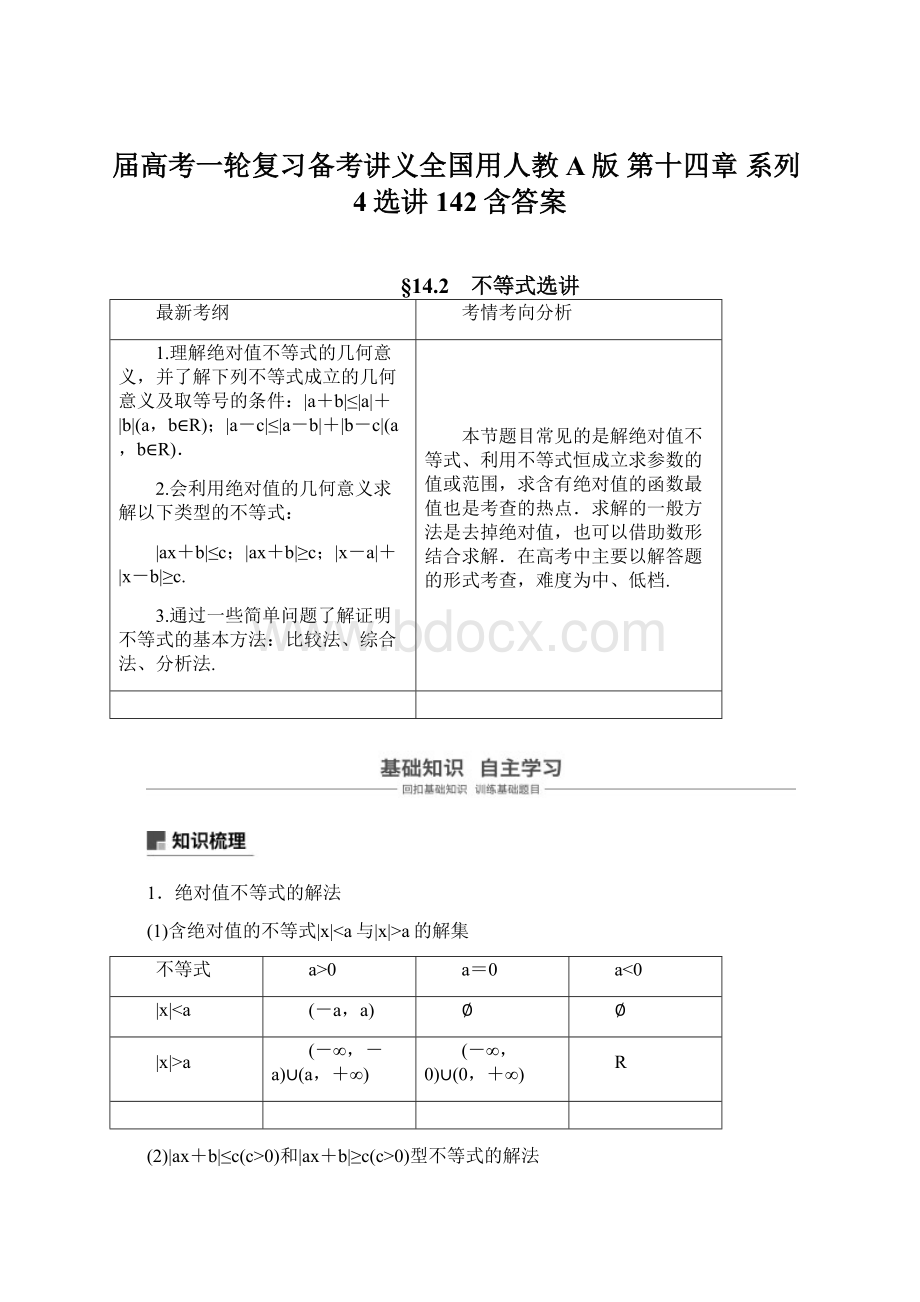
|x|>

（－∞，－a）∪（a，＋∞）

（－∞，0）∪（0，＋∞）

R

（2）|ax＋b|≤c（c>

0）和|ax＋b|≥c（c>

0）型不等式的解法

①|ax＋b|≤c⇔－c≤ax＋b≤c；

②|ax＋b|≥c⇔ax＋b≥c或ax＋b≤－c.

（3）|x－a|＋|x－b|≥c（c>

0）和|x－a|＋|x－b|≤c（c>

①利用绝对值不等式的几何意义求解，体现了数形结合的思想；

②利用“零点分段法”求解，体现了分类讨论的思想；

③通过构造函数，利用函数的图象求解，体现了函数与方程的思想．

2．含有绝对值的不等式的性质

（1）如果a，b是实数，则|a|－|b|≤|a±

b|≤|a|＋|b|，当且仅当ab≥0时，等号成立．

（2）如果a，b，c是实数，那么|a－c|≤|a－b|＋|b－c|，当且仅当（a－b）（b－c）≥0时，等号成立．

3．不等式证明的方法

（1）比较法

①作差比较法

知道a>

b⇔a－b>

0，a<

b⇔a－b<

0，因此要证明a>

b，只要证明a－b>

0即可，这种方法称为作差比较法．

②作商比较法

由a>

b>

0⇔>

1且a>

0，b>

0，因此当a>

0时，要证明a>

b，只要证明>

1即可，这种方法称为作商比较法．

（2）综合法

从已知条件出发，利用不等式的有关性质或定理，经过推理论证，最终推导出所要证明的不等式成立，这种证明方法叫做综合法，即“由因导果”的方法．

（3）分析法

从待证不等式出发，逐步寻求使它成立的充分条件，直到将待证不等式归结为一个已成立的不等式（已知条件、定理等），从而得出要证的不等式成立，这种证明方法叫做分析法，即“执果索因”的方法．

题组一　思考辨析

1．判断下列结论是否正确（请在括号中打“√”或“×

”）

（1）若|x|>

c的解集为R，则c≤0.（　×

　）

（2）不等式|x－1|＋|x＋2|<

2的解集为∅.（　√　）

（3）对|a＋b|≥|a|－|b|当且仅当a>

0时等号成立．（　×

（4）对|a|－|b|≤|a－b|当且仅当|a|≥|b|时等号成立．（　×

（5）对|a－b|≤|a|＋|b|当且仅当ab≤0时等号成立．（　√　）

题组二　教材改编

2．[P20T7]不等式3≤|5－2x|<

9的解集为（　　）

A．[－2,1）∪[4,7）B．（－2,1]∪（4,7]

C．（－2，－1]∪[4,7）D．（－2,1]∪[4,7）

答案　D

解析　由题意得

即

解得不等式的解集为（－2,1]∪[4,7）．

3．[P20T8]求不等式|x－1|－|x－5|<

2的解集．

解　①当x≤1时，原不等式可化为1－x－（5－x）<

2，

∴－4<

2，不等式恒成立，∴x≤1；

②当1<

x<

5时，原不等式可化为x－1－（5－x）<

∴x<

4，∴1<

4；

③当x≥5时，原不等式可化为x－1－（x－5）<

2，该不等式不成立．

综上，原不等式的解集为（－∞，4）．

题组三　易错自纠

4．若函数f（x）＝|x＋1|＋2|x－a|的最小值为5，则实数a＝________.

答案　4或－6

解析　方法一　①当a＝－1时，f（x）＝3|x＋1|，

f（x）min＝0，不符合题意；

②当a<

－1时，f（x）＝

∴f（x）min＝f（a）＝－a－1＝5，∴a＝－6成立；

③当a>

∴f（x）min＝f（a）＝a＋1＝5，∴a＝4成立．

综上，a＝4或a＝－6.

方法二　当a＝－1时，f（x）min＝0，不符合题意；

当a≠－1时，f（x）min＝f（a）＝|a＋1|＝5，

∴a＝4或a＝－6.

5．已知a，b，c是正实数，且a＋b＋c＝1，则＋＋的最小值为________．

答案　9

解析　把a＋b＋c＝1代入到＋＋中，

得＋＋

＝3＋＋＋

≥3＋2＋2＋2＝9，

当且仅当a＝b＝c＝时，等号成立．

6．若不等式|2x－1|＋|x＋2|≥a2＋a＋2对任意实数x恒成立，则实数a的取值范围为______________．

答案　

解析　设y＝|2x－1|＋|x＋2|

＝

当x<

－2时，y＝－3x－1>

5；

当－2≤x<

时，y＝－x＋3>

，y≤5；

当x≥时，y＝3x＋1≥，故函数y＝|2x－1|＋|x＋2|的最小值为.因为不等式|2x－1|＋|x＋2|≥a2＋a＋2对任意实数x恒成立，所以≥a2＋a＋2.

解不等式≥a2＋a＋2，得－1≤a≤，

故实数a的取值范围为.

题型一　绝对值不等式的解法

1．（2017·

全国Ⅰ）已知函数f（x）＝－x2＋ax＋4，g（x）＝|x＋1|＋|x－1|.

（1）当a＝1时，求不等式f（x）≥g（x）的解集；

（2）若不等式f（x）≥g（x）的解集包含[－1,1]，求a的取值范围．

解　

（1）当a＝1时，不等式f（x）≥g（x）等价于

x2－x＋|x＋1|＋|x－1|－4≤0.①

－1时，①式化为x2－3x－4≤0，无解；

当－1≤x≤1时，①式化为x2－x－2≤0，

从而－1≤x≤1；

当x>

1时，①式化为x2＋x－4≤0，

从而1<

x≤.

所以f（x）≥g（x）的解集为.

（2）当x∈[－1,1]时，g（x）＝2，

所以f（x）≥g（x）的解集包含[－1,1]等价于

当x∈[－1,1]时，f（x）≥2.

又f（x）在[－1,1]上的最小值必为f（－1）与f

（1）之一，

所以f（－1）≥2且f

（1）≥2，得－1≤a≤1.

所以a的取值范围为[－1,1]．

2．已知函数f（x）＝|x＋1|－2|x－a|，a>

0.

（1）当a＝1时，求不等式f（x）>

1的解集；

（2）若f（x）的图象与x轴围成的三角形的面积大于6，求a的取值范围．

解　

（1）当a＝1时，

f（x）>

1化为|x＋1|－2|x－1|－1>

当x≤－1时，不等式化为x－4>

0，无解；

当－1<

1时，不等式化为3x－2>

0，解得<

1；

当x≥1时，不等式化为－x＋2>

0，解得1≤x<

2.

所以f（x）>

1的解集为.

（2）由题设可得，f（x）＝

所以函数f（x）的图象与x轴围成的三角形的三个顶点分别为A，B（2a＋1,0），C（a，a＋1），

△ABC的面积为（a＋1）2.

由题设得（a＋1）2>

6，故a>

所以a的取值范围为（2，＋∞）．

思维升华解绝对值不等式的基本方法

（1）利用绝对值的定义，通过分类讨论转化为解不含绝对值符号的普通不等式．

（2）当不等式两端均为正号时，可通过两边平方的方法，转化为解不含绝对值符号的普通不等式．

（3）利用绝对值的几何意义，数形结合求解．

题型二　利用绝对值不等式求最值

典例

（1）对任意x，y∈R，求|x－1|＋|x|＋|y－1|＋|y＋1|的最小值；

（2）对于实数x，y，若|x－1|≤1，|y－2|≤1，求|x－2y＋1|的最大值．

解　

（1）∵x，y∈R，

∴|x－1|＋|x|≥|（x－1）－x|＝1，

当且仅当0≤x≤1时等号成立，

∴|y－1|＋|y＋1|≥|（y－1）－（y＋1）|＝2，

当且仅当－1≤y≤1时等号成立，

∴|x－1|＋|x|＋|y－1|＋|y＋1|≥1＋2＝3，

当且仅当0≤x≤1，－1≤y≤1同时成立时等号成立．

∴|x－1|＋|x|＋|y－1|＋|y＋1|的最小值为3.

（2）|x－2y＋1|＝|（x－1）－2（y－1）|≤|x－1|＋|2（y－2）＋2|≤1＋2|y－2|＋2≤5，即|x－2y＋1|的最大值为5.

思维升华求含绝对值的函数最值时，常用的方法有三种

（1）利用绝对值的几何意义．

（2）利用绝对值三角不等式，即|a|＋|b|≥|a±

b|≥|a|－|b|.

（3）利用零点分区间法．

跟踪训练（2017·

西安模拟）已知a和b是任意非零实数．

（1）求的最小值；

（2）若不等式|2a＋b|＋|2a－b|≥|a|（|2＋x|＋|2－x|）恒成立，求实数x的取值范围．

解　

（1）∵≥＝＝4，

当且仅当（2a＋b）（2a－b）≥0时等号成立，

∴的最小值为4.

（2）若不等式|2a＋b|＋|2a－b|≥|a|（|2＋x|＋|2－x|）恒成立，即|2＋x|＋|2－x|≤恒成立，

故|2＋x|＋|2－x|≤min.

由

（1）可知，的最小值为4，

∴x的取值范围即为不等式|2＋x|＋|2－x|≤4的解集．

解不等式得－2≤x≤2，

故实数x的取值范围为[－2,2]．

题型三　绝对值不等式的综合应用

典例已知函数f（x）＝|x－a|＋（a≠0）．

（1）若不等式f（x）－f（x＋m）≤1恒成立，求实数m的最大值；

（2）当a<

时，函数g（x）＝f（x）＋|2x－1|有零点，求实数a的取值范围．

解　

（1）∵f（x）＝|x－a|＋（a≠0），

∴f（x＋m）＝|x＋m－a|＋，

∴f（x）－f（x＋m）＝|x－a|－|x＋m－a|≤1，

又|x－a|－|x＋m－a|≤|m|，

∴|m|≤1，∴－1≤m≤1，

∴实数m的最大值为1.

时，

g（x）＝f（x）＋|2x－1|＝|x－a|＋|2x－1|＋

∴g（x）min＝g＝－a＋

＝≤0，

∴或

∴－≤a<

0，

∴实数a的取值范围是.

思维升华

（1）解决与绝对值有关的综合问题的关键是去掉绝对值，化为分段函数来解决．

（2）数形结合是解决与绝对值有关的综合问题的常用方法．

全国Ⅲ）已知函数f（x）＝|x＋1|－|x－2|.

（1）求不等式f（x）≥1的解集；

（2）若不等式f（x）≥x2－x＋m的解集非空，求m的取值范围．

解　

（1）f（x）＝

当x＜－1时，f（x）≥1无解；

当－1≤x≤2时，由f（x）≥1，得2x－1≥1，解得1≤x≤2；

当x＞2时，由f（x）≥1，解得x＞2，

所以f（x）≥1的解集为{x|x≥1}．

（2）由f（x）≥x2－x＋m，得

m≤|x＋1|－|x－2|－x2＋x.

而|x＋1|－|x－2|－x2＋x

≤|x|＋1＋|x|－2－x2＋|x|

＝－2＋≤，

当x＝时，|x＋1|－|x－2|－x2＋x＝.

故m的取值范围为.

题型四　用综合法与分析法证明不等式

典例

（1）已知x，y均为正数，且x>

y，求证：

2x＋≥2y＋3；

（2）设a，b，c>

0且ab＋bc＋ca＝1，求证：

a＋b＋c≥.

证明　

（1）因为x>

0，y>

0，x－y>

2x＋－2y＝2（x－y）＋

＝（x－y）＋（x－y）＋

≥3＝3，

所以2x＋≥2y＋3.

（2）因为a，b，c>

所以要证a＋b＋c≥，

只需证明（a＋b