十大高中平面几何几何定理汇总及证明供参考.docx
《十大高中平面几何几何定理汇总及证明供参考.docx》由会员分享,可在线阅读,更多相关《十大高中平面几何几何定理汇总及证明供参考.docx(25页珍藏版)》请在冰豆网上搜索。
十大高中平面几何几何定理汇总及证明供参考
高中平面几何定理汇总及证明
1.共边比例定理
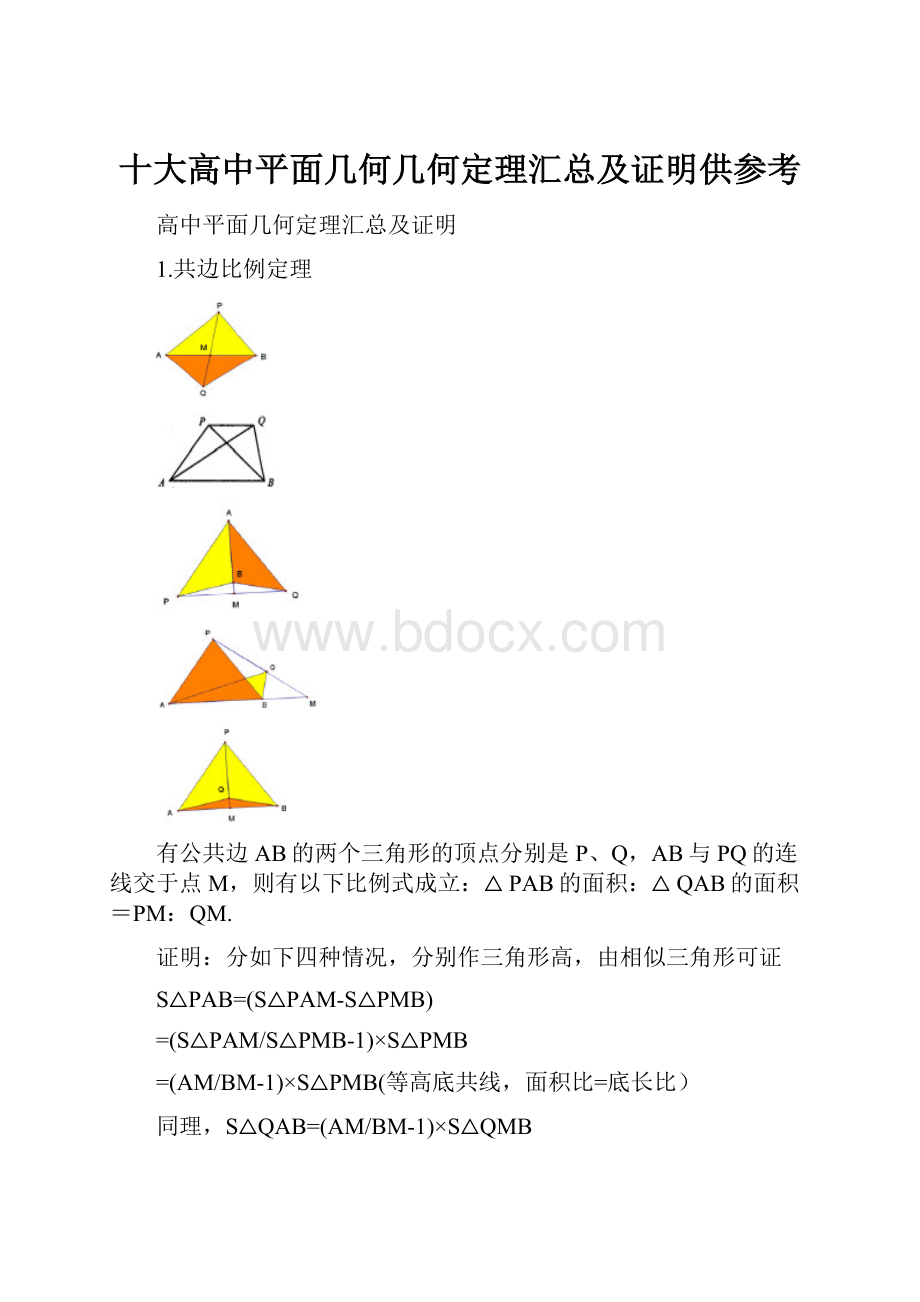
有公共边AB的两个三角形的顶点分别是P、Q,AB与PQ的连线交于点M,则有以下比例式成立:
△PAB的面积:
△QAB的面积=PM:
QM.
证明:
分如下四种情况,分别作三角形高,由相似三角形可证
S△PAB=(S△PAM-S△PMB)
=(S△PAM/S△PMB-1)×S△PMB
=(AM/BM-1)×S△PMB(等高底共线,面积比=底长比)
同理,S△QAB=(AM/BM-1)×S△QMB
所以,S△PAB/S△QAB=S△PMB/S△QMB=PM/QM(等高底共线,面积比=底长比)
定理得证!
特殊情况:
当PB∥AQ时,易知△PAB与△QAB的高相等,从而S△PAB=S△QAB,反之,S△PAB=S△QAB,则PB∥AQ。
2.正弦定理
在任意一个平面三角形中,各边和它所对角的值的比相等且等于外接圆半径的2倍”,即a/sinA = b/sinB =c/sinC =2r=R(r为外接圆半径,R为直径)
证明:
现将△ABC,做其,设为O。
我们考虑∠C及其对边AB。
设AB长度为c。
若∠C为直角,则AB就是⊙O的直径,即c=2r。
∵
(特殊角正弦函数值)
∴
若∠C为锐角或钝角,过B作直径BC`交⊙O于C`,连接C'A,显然BC'=2r=R。
若∠C为,则C'与C落于AB的同侧,
此时∠C'=∠C(同弧所对的圆周角相等)
∴在Rt△ABC'中有
若∠C为,则C'与C落于AB的异侧,BC的对边为a,此时∠C'=∠A,亦可推出
。
考虑同一个三角形内的三个角及三条边,同理,分别列式可得
。
3.
分角定理
在△ABC中,D是边BC上异于B,C或其延长线上的一点,连结AD,则有BD/CD=(sin∠BAD/sin∠CAD)*(AB/AC)。
证明:
S△ABD/S△ACD=BD/CD…………
S△ABD/S△ACD=[(1/2)×AB×AD×sin∠BAD]/[(1/2)×AC×AD×sin∠CAD]
=(sin∠BAD/sin∠CAD)×(AB/AC) …………
由式和式得
BD/CD=(sin∠BAD/sin∠CAD)×(AB/AC)
4.张角定理
在△ABC中,D是BC上的一点,连结AD。
那么
。
证明:
设∠1=∠BAD,∠2=∠CAD
由,
S△ABD/S△ABC=BD/BC=(AD/AC)*(sin∠1/sin∠BAC)
→(BD/BC)*(sin∠BAC/AD)=sin∠1/AC
S△ACD/S△ABC=CD/BC=(AD/AB)*(sin∠2/sin∠BAC)
→(CD/BC)*(sin∠BAC/AD)=sin∠2/AB
式+式即得sin∠1/AC+sin∠2/AB=sin∠BAC/AD
5.帕普斯定理
直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD交于G,AF,DC交于I,BF,EC交于H,则G,I,H共线。
6.
蝴蝶定理
设S为圆内AB的中点,过S作弦CF和DE。
设CF和DE各相交AB于点M和N,则S是MN的中点。
证明:
过O作OL⊥ED,OT⊥CF,垂足为L、T,
连接ON,OM,OS,SL,ST,易明△ESD∽△CSF
∴ES/CS=ED/FC
根据垂径定理得:
LD=ED/2,FT=FC/2
∴ES/CS=EL/CT
又∵∠E=∠C
∴△ESL∽△CST
∴∠SLN=∠STM
∵S是AB的中点所以OS⊥AB
∴∠OSN=∠OLN=90°
∴O,S,N,L四点共圆,(一中同长)
同理,O,T,M,S四点共圆
∴∠STM=∠SOM,∠SLN=∠SON
∴∠SON=∠SOM
∵OS⊥AB
∴MS=NS
7.西姆松定理
过三角形上异于三角形顶点的任意一点作三边或其延长线上的,则三共线。
(此线常称为西姆松线)。
证明:
若L、M、N三点共线,连结BP,CP,则因PL⊥BC,PM⊥AC,PN⊥AB,有B、L、P、N和P、M、C、L分别四点共圆,有
∠NBP=∠NLP=∠MLP=∠MCP.
故A、B、P、C四点共圆。
若A、P、B、C四点共圆,则
∠NBP=∠MCP。
因PL⊥BC,PM⊥AC,PN⊥AB,
有B、L、P、N和P、M、C、L四点共圆,有
∠NBP=∠NLP=∠MCP=∠MLP.
故L、M、N三点共线。
西姆松:
若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上。
证明:
PM⊥AC,PN⊥AB,所以A,M,N,P共圆
8.清宫定理
设P、Q为△ABC的外接圆上异于A、B、C的两点,P关于三边BC、CA、AB的对称点分别是U、V、W,且QU、QV、QW分别交三边BC、CA、AB或其延长线于D、E、F,则D、E、F在同一直线上.
证明:
A、B、P、C,因此
∠PCE=∠ABP
点P和V关于CA
所以∠PCV=2∠PCE
又因为P和W关于AB对称,所以
∠PBW=2∠ABP
从这三个式子,有
∠PCV=∠PBW
另一方面,因为∠PCQ和∠PBQ都是弦PQ所对的,所以
∠PCQ=∠PBQ
两式相加,有
∠PCV+∠PCQ=∠PBW+∠PBQ
即∠QCV=∠QBW
即△QCV和△QBW有一个顶角相等,因此
但是
,
,所以
同理
,
于是
根据梅涅劳斯定理的逆定理,D、E、F三点在同一直线上。
9.密克定理
三圆定理:
设三个圆C1,C2,C3交于一点O,而M,N,P分别是C1和C2,C2和C3,C3和C1的另一交点。
设A为C1的点,直线MA交C2于B,直线PA交C3于C。
那么B,N,C这三点共线。
逆定理:
如果是三角形,M,N,P三点分别在边AB,BC,CA上,那么△AMP、△BMN、△CPN的外接圆交于一点O。
完全四线形定理
如果ABCDEF是完全四线形,那么三角形的外接圆交于一点O,称为密克点。
四圆定理
设C1,C2,C3,C4为四个圆,A1和B1是C1和C2的交点,
A2和B2是C2和C3的交点,A3和B3是C3和C4的交点,
A4和B4是C1和C4的交点。
那么A1,A2,A3,A4四点共圆当且仅当B1,B2,B3,B4四点共圆。
证明:
在△ABC的BC,AC,AB边上分别取点W,M,N,对AMN,△BWN和△CWM分别作其外接圆,则这三个外接圆共点。
该定理的证明很简单,利用“圆内接四边形对角和为180度”及其逆定理。
现在已知U是
和
的公共点。
连接UM和UN,
∵四边形BNUW和四边形CMUW分别是
和
的内接四边形,
∴∠UWB+∠UNB=∠UNB+∠UNA=180度
∴∠UWB=∠UNA。
同理∠UWB+∠UWC=∠UWC+∠UMC=180度
∴∠UWB=∠UMC。
∵∠UMC+∠UMA=180度
∴∠UNA+∠UMA=180度,
这正说明四边形ANUM是一个圆内接四边形,而该圆必是
,U必在
上。
10.婆罗摩笈多定理
圆内接四边形ABCD的对角线AC⊥BD,垂足为M。
EF⊥BC,且M在EF上。
那么F是AD的中点。
证明:
∵AC⊥BD,ME⊥BC
∴∠=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同时∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中点
逆定理:
若的对角线相互垂直,则一边中点与对角线交点的连线垂直于对边。
证明:
∵MA⊥MD,F是AD中点
∴AF=MF
∴∠CAD=∠AMF
∵∠CAD=∠,∠AMF=∠CME
∴∠CBD=∠CME
∵∠CME+∠BME=∠BMC=90°
∴∠CBD+∠BME=90°
∴EF⊥BC
11.托勒密定理
圆内接中,两条的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).圆内接四边形ABCD,求证:
AC·BD=AB·CD+AD·BC.
证明:
过C作CP交BD于P,使∠1=∠2,又∠3=∠4,
∴△ACD∽△BCP.
得AC:
BC=AD:
BP,AC·BP=AD·BC①。
又∠ACB=∠DCP,∠5=∠6,
∴△ACB∽△DCP.得AC:
CD=AB:
DP,AC·DP=AB·CD②。
1+②得AC(BP+DP)=AB·CD+AD·BC.
即AC·BD=AB·CD+AD·BC.
12.梅涅劳斯定理
当交
三边所在直线
于点
时,
。
证明:
过点C作CP∥DF交AB于P,则
两式相乘得
梅涅劳斯逆定理:
若有三点F、D、E分别在边三角形的三边AB、BC、CA或其延长线上,且满足AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线。
证明:
先假设E、F、D三点不共线,直线DE与AB交于P。
由梅涅劳斯定理的定理证明(如利用平行线分线段成比例的证明方法)得:
(AP/PB)(BD/DC)(CE/EA)=1。
∵(AF/FB)(BD/DC)(CE/EA)=1。
∴AP/PB=AF/FB;
∴(AP+PB)/PB=(AF+FB)/FB;
∴AB/PB=AB/FB;
∴PB=FB;即P与F重合。
∴D、E、F三点共线。
13.塞瓦定理
在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则
(BD/DC)×(CE/EA)×(AF/FB)=1。
∵△ADC被直线BOE所截,
∴(CB/BD)*(DO/OA)*(AE/EC)=1①
∵△ABD被直线COF所截,
∴(BC/CD)*(DO/OA)*(AF/FB)=1②
2/①约分得:
(DB/CD)×(CE/EA)×(AF/FB)=1
14.圆幂定理
相交弦定理:
如图Ⅰ,AB、CD为圆O的两条任意弦。
相交于点P,连接AD、BC,由于∠B与∠D同为弧AC所对的圆周角,因此由知:
∠B=∠D,同理∠A=∠C,所以
。
所以有:
,即:
。
割线定理:
如图Ⅱ,连接AD、BC。
可知∠B=∠D,又因为∠P为公共角,所以有
,同上证得
。
切割线定理:
如图Ⅲ,连接AC、AD。
∠PAC为切线PA与弦AC组成的弦切角,因此有∠PBC=∠D,又因为∠P为公共角,所以有
,易证
图Ⅳ,PA、PC均为切线,则∠PAO=∠PCO=90°,在直角三角形中:
OC=OA=R,PO为公共边,因此
。
所以PA=PC,所以
。
综上可知,
是普遍成立的。
弦切角定理:
的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数。
点对圆的幂
P点对圆O的幂定义为
点P在圆O内→P对圆O的幂为负数;
点P在圆O外→P对圆O的幂为正数;
点P在圆O上→P对圆O的幂为0。
:
:
三条内的
外心:
三角形三条边的垂直平分线(中垂线)的相交点
重心:
三角形三边中线的交点
:
的三条的交点
旁心:
三角形的(与三角形的一边和其他两边的延长线的圆)的圆心
九点圆心:
三角形三边的,三高的垂足和三个欧拉点〔连结三角形各顶点与垂心所得三线段的中点〕九点共圆的圆心
15.根心定理
三个两两不同心的,形成三条根,则必有下列三种情况之一:
(1)三根轴两两平行;
(2)三根轴完全重合;
(3)三根轴两两相交,此时三根轴必汇于一点,该点称为三圆的根心。
平面上任意三个圆,若这三个圆不共线,则三条根轴相交于一点,这个点叫它们的根心;若三圆圆心共线,则三条根轴互相平行。
根轴定义:
A与B的L1:
到A与B的切线相等的点。
B与C的根轴L2:
到B与C的切线相等的点。
证明
设A、B、C三个圆,圆心不重合也不共线。
考察L1与L2的交点P。
因为P在L1上,所以:
P到A的切线距离=P到B的切线距离。
因为P在L2上,所以:
P到B的切线距离=P到C的切线距离。
所以:
P到A的切线距离=P到B的切线距离=P到C的切线距离。
也就是:
P到A的切线距离=P到C的切线距离。
所以:
P在A与C的根轴上。
所以:
三个根轴交于一点。
16.鸡爪定理
设△ABC的为I,∠A内的为J,AI的延长线交三角形于K,则KI=KJ=KB=KC。
证明:
由内心和旁心的定义可知∠IBC=∠ABC/2,∠JBC=(180°-∠ABC)/2
∴∠IBC+∠JBC=∠ABC/2+90°-∠ABC/2=90°=∠IBJ
同理,∠ICJ=90°
∵∠IBJ+∠ICJ=180°
∴IBJC,且IJ为圆的直径
∵AK平分∠BAC
∴KB=KC(相等的所对的弦相等)
又∵∠IBK=∠IBC+∠KBC=∠ABC/2+∠KAC=∠ABI+∠BAK=∠KIB
∴KB=KI
由可知K是IJ的中点
∴KB=KI=KJ=KC
逆定理:
设△ABC中∠BAC的平分线交△ABC的于K。
在AK及延长线上截取KI=KB=KJ,其中I在△ABC的内部,J在△ABC的外部。
则I是△ABC的内心,J是△ABC的。
证明:
利用可轻松证明该定理的。
取△ABC的内心I'和旁心J’,根据定理有KB=KC=KI'=KJ'
又∵KB=KI=KJ
∴I和I'重合,J和J’重合
即I和J分别是内心和旁心
17.费尔巴哈定理
三角形的九点圆与其内切圆以及三个旁切圆相切
设△ABC的内心为I,九点圆的圆心为V。
三边中点分别为L,M,N,内切圆与三边的切点分别是P,Q,R,三边上的垂足分别为D,E,F。
不妨设AB>AC。
假设⊙I与⊙V相切于点T,那么LT与⊙I相交,设另一个交点为S。
过点S作⊙I的切线,分别交AB和BC于V,U,连接AU。
又作两圆的公切线TX,使其与边AB位于LT的同侧。
由假设知
∠XTL=∠LDT
而TX和SV都是⊙I的切线,且与弦ST所夹的圆弧相同,于是
∠XTL=∠VST
因此
∠LDT=∠VST
则
∠UDT+∠UST=180°
这就是说,S,T,D,U共圆。
而这等价于:
LU×LD=LS×LT
又LP²=LS×LT
故有LP²=LU×LD
另一方面,T是公共的切点,自然在⊙V上,
因此L,D,T,N共圆,进而有
∠LTD=∠LND
由已导出的S,T,D,U共圆,得
∠LTD=∠STD=180°-∠SUD=∠VUB
=∠AVU-∠B
而
∠LND=∠NLB-∠NDB
=∠ACB-∠NBD
=∠C-∠B
(这里用了LN∥AC,以及直角三角形斜边上中线等于斜边的一半)
所以,就得到
∠AVU=∠C
注意到AV,AC,CU,UV均与⊙I相切,于是有
∠AIR=∠AIQ
∠UIS=∠UIP
∠RIS=∠QIS
三式相加,即知
∠AIU=180°
也即是说,A,I,U三点共线。
另外,AV=AC,这可由△AIV≌△AIC得到。
(这说明,公切点T可如下得到:
连接AI,并延长交BC于点U,
过点U作⊙I的切线,切点为S,交AB于V,
最后连接LS,其延长线与⊙I的交点即是所谓的公切点T。
)
连接CV,与AU交于点K,
则K是VC的中点。
前面已得到:
LP²=LU×LD
而
2LP=(BL+LP)-(CL-LP)
=BP-CP
=BR-CQ
=(BR+AR)-(CQ+AQ)
=AB-AC
=AB-AV
=BV
即LP=
BV
然而
LK是△CBV的中位线
于是LK=
BV
因之LP=LK
故LK²=LU×LD
由于以上推导均可逆转,因此我们只需证明:
LK²=LU×LD。
往证之
这等价于:
LK与圆KUD相切
于是只需证:
∠LKU=∠KDU
再注意到LK∥AB(LK是△CBV的中位线),即有
∠LKU=∠BAU
又AU是角平分线,于是
∠LKU=∠CAU=∠CAK
于是又只需证:
∠CAK=∠KDU
即证:
∠CAK+∠CDK=180°
这即是证:
A,C,D,K四点共圆
由于AK⊥KC(易得),AD⊥DC
所以A,C,D,K确实共圆。
这就证明了⊙I与⊙V内切。
旁切圆的情形是类似的。
证毕
另略证:
OI2=R2-2Rr
IH2=2r2-2Rr'
OH2=R2-4Rr'(其中r‘是垂心H的垂足三角形的内切圆半径,R、r是三角形ABC外接圆和内切圆半径)
FI2=1/2(OI2+IH2)-1/4OH2=(1/2R-r)2
FI=1/2R-r这就证明了九点圆与内切圆内切(九点圆半径为外接圆半径一半。
F是九点圆圆心,I为内心)
18.莫利定理
将三角形的三个内角三等分,靠近某边的两条三分角线相交得到一个交点,则这样的三个交点可以构成一个正三角形
证明:
设△ABC中,AQ,AR,BR,BP,CP,CQ为各角的三等分线,三边长为a,b,c,三内角为3α,3β,3γ,则α+β+γ=60°。
在△ABC中,由,得AF=csinβ/sin(α+β)。
不失一般性,△ABC直径为1,则由正弦定理,知c=sin3γ,所以
AF=(sin3γ*sinβ)/sin(60°-γ)
=[sinβ*sinγ(3-4sin²γ)]/[1/2(√3cosγ-sinγ)]
=2sinβsinγ(√3cosγ+sinγ)
=4sinβsinγsin(60°+γ).
同理,AE=4sinβsinγsin(60°+β)
∴AF:
AE=[4sinβsinγsin(60°+γ)]:
[4sinβsinγsin(60°+β)]
=sin(60°+γ):
sin(60°+β)=sin∠AEF:
sin∠AFE
∴∠AEF=60°+γ,∠AFE=60°+β.同理得,∠CED=60°+α
∠FED=180°-CED-(AEF-α-γ)=180°-60°-α-60°+α=60°
∴△FED为
19.拿破仑定理
若以任意三角形的各边为底边向形外作底角为60°的等腰三角形,则它们的中心构成一个等边三角形。
在△ABC的各边上向外各作等边△ABF,等边△ACD,等边△BCE。
证明:
设等边△ABF的和等边△ACD的外接圆相交于O;连AO、CO、BO。
∴∠AFB=∠ADC=60°;
∵A、F、B、O;A、D、C、O;
∴∠AOB=∠AOC=120°;
∴∠BOC=120°;
∵△BCE是
∴∠BEC=60°;
∴B、E、C、O;
∴这3个等边三角形的外接圆共点。
∵A、D、B、O四点共圆
A、F、C、O
B、E、C、O
∠AFC=∠ADB=∠BEC=60°;
∴∠AOB=∠AOC=∠BOC=120°;
∵NP、MP、MN是;
BO、CO、AO是;
∴BO⊥NP于X;
CO⊥MP于Y;
AO⊥NM于Z。
∴X、P、Y、O;
Y、M、Z、O;
Z、N、X、O;
∴∠N=∠M=∠P=60°;
即△MNP是。