数据结构实验报告管道铺设问题.docx
《数据结构实验报告管道铺设问题.docx》由会员分享,可在线阅读,更多相关《数据结构实验报告管道铺设问题.docx(26页珍藏版)》请在冰豆网上搜索。
数据结构实验报告管道铺设问题
《计算机软件技术基础》实验报告I—数据结构
实验三:
管道铺设施工的最正确方案问题
一、问题描述
1.实验题目:
需要在某个城市n个居民小区之间铺设煤气管道,则在这n个居民小区之间只需要铺设n-1条管道即可。
假设任意两个小区之间都可以铺设管道,但由于地理环境不同,所需要的费用也不尽相同。
选择最优的方案能使总投资尽可能小,这个问题即为求无向网的最小生成树。
2.基本要求:
在可能假设的m条管道中,选取n-1条管道,使得既能连通n个小区,又能使总投资最小。
每条管道的费用以网中该边的权值形式给出,网的存储采用邻接表的结构。
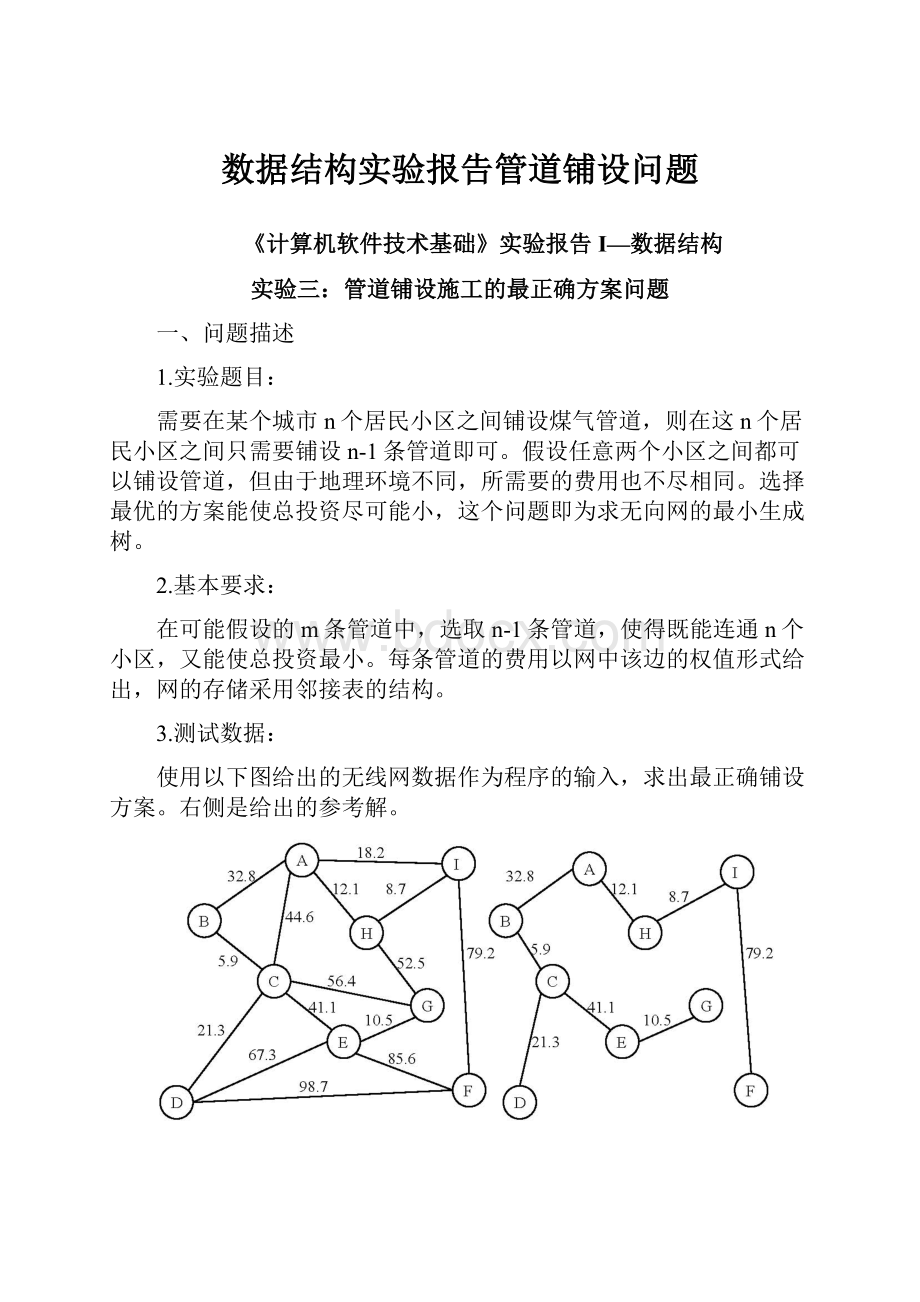
3.测试数据:
使用以下图给出的无线网数据作为程序的输入,求出最正确铺设方案。
右侧是给出的参考解。
图1小区煤气管道铺设网与其参考解
4.输入输出:
从键盘或文件读入上图中的无向网,以顶点对(i,j)的形式输出最小生成树的边。
二、需求分析
1.本程序所能达到的基本可能:
本程序用无向网表示各小区之间的管道铺设情况,结点表示小区位置,边表示铺设的管道,边的权值表示各段的费用。
采用邻接表存储,输入无向网数据创建邻接表,通过普利姆算法求出最小生成树,即是最正确铺设方案。
2.输入输出形式与输入值围:
根据提示输入总的边数,结点数。
再根据提示输入各结点的信息即结点的名称,输入边的信息,即边的两个端点和该边的权值。
输入后成功创建邻接表,自动输出所建立的邻接表和普利姆算法求出的最小生成树。
3.测试数据要求:
使用以下图给出的无线网数据作为程序的输入,求出最正确铺设方案。
右侧是给出的参考解。
输入结点数和边数:
915
根据提示分别输入九个结点的名称:
ABCDEFGHI
输入边的信息,即两个端点的名称与该边的权值:
(AB32.8);(BC5.9);(CD21.3);(DE67.3);
(AC44.6);(AH12.1);(AI18.2);(HI8.7);(HG52.5);(CG56.4);(CE41.1);(EF85.6);
(DF98.7);(IF79.2);(EG10.5)
输入完毕直接输出“建立的图邻接表表示为:
0->8->7->2->1->2->0->2->4->6->0->3->1->3->5->4->2->4->6->5->2->3->5->8->3->4->6->4->2->7->7->6->8->0->8->5->7->0”
直接输出应用prime算法,得到的最小生成树的结果,用结点字母表示
三、概要设计
为了实现上述功能,该程序以邻接表存储的无向图模拟居民住宅的分布和住宅之间的管道,通过普利姆算法求最小生成树来求解管道最小花费。
因此需要邻接表这一抽象数据类型来表示无向图。
还需要普利姆算法求最小生成树。
1.邻接表抽象数据类型定义
ADT ALGraph{
数据对象:
D={ai,bi,ci|ai∈AdjList,bi∈int,ci∈int),i=1,2...,n,n≥0}:
数据关系:
R=∅
基本操作:
create(ALGraph*G)//建立无向图的邻接表存储
voidprime(ALGraph*G,intfrom)//用普利姆算法求最小生成树
}ADT ALGraph
2.ADT的c语言形式说明:
typedefstruct
{
AdjListadjlist;//邻接表
intn,e;//顶点数和边数
}ALGraph;//ALGraph是以邻接表方式存储的图类型
voidcreate(ALGraph*G)//建立无向图的邻接表存储
voidprime(ALGraph*G,intfrom)//用普利姆算法求最小生成树
3.本程序保护模块:
主函数模块
图模块
4.普利姆算法分析
(1)普利姆算法思想:
普利姆算法的思想是:
在图中人去一个定点k0作为开始点,令U={k0},W=V-U,
其中V为图中所有顶点集,然后找一个顶点在U中,另一个顶点在w中的边中最短
的一条,找到后,将该边作为最小生成树的树边保存起来,并将该边顶点全部加入U集合中,并从W中删除这些顶点,然后重新调整U中顶点到W中顶点的距离,使之保持最小,再重复此过程,直到W为空集。
(2)算法过程描述:
在图G=(V,E)(V是顶点,E是边)中,从集合V中任取一个顶点,如k0放入集合U中,这时,U={k0},集合T(E)为空。
从k0出发寻找与U中顶点相邻权值最小的边的另一顶点k1,并使k1加入U。
即U={k0,k1},同时将该边加入集合T(E)中。
重复
(2),直到U=V为止。
这时T(E)中有n-1条边,T=(U,T(E))就是一一颗最小生成树。
5.主程序流程与其模块调用关系:
(1)主程序流程:
先提示用户输入相关数据:
节点数,边数,各结点名称,各边两端名称和边的权值。
创建邻接表存储无向图并输出这一邻接表。
用普利姆算法求最小生成树:
访问各节点,从已经访问过的节点和未访问过的节点组成的所有边中挑出权重最小的一条边放入邻接表EdgeNode*minEdge中。
输出这个最小权重的表。
(2)模块调用关系
(3)功能模块图
6.主要算法流程图
create(ALGraph*G)
四、详细设计
1、元素类型、结点类型、结点指针类型:
typedefstructnode//边表节点
{
intsrc;//边端的序号
charsrcName;//边端的名称
intadjvex;//邻接点域
node*next;//指向下一个邻接点的指针域
charadjName;
floatcost;//边的权值
}EdgeNode;
typedefstruct//顶点表节点
{
charvertex;//顶点域
EdgeNode*firstedge;//边表头指针
}VertexNode;
typedefVertexNodeAdjList[MaxVertexNum];//AdjList是邻接表类型
typedefstruct
{
AdjListadjlist;//邻接表
intn,e;//顶点数和边数
}ALGraph;//ALGraph是以邻接表方式存储的图类型
2.创建邻接表
voidcreate(ALGraph*G)//建立无向图的邻接表存储
{
intk,w,v;
EdgeNode*s;
cout<<"请输入节点数和边数(用空格隔开)"<cin>>G->n>>G->e;//读入顶点数和边数
for(inti=0;in;i++)//建立有n个顶点的顶点表
{
cout<<"请输入顶点名称:
";
charc;
cin>>c;//读入顶点信息
G->adjlist[i].vertex=c;
G->adjlist[i].firstedge=NULL;//顶点表的边表头指针设为空
}
printf("建立边表\n");
for(k=0;ke;k++)//建立边表
{
floatcost;
cout<<"请输入边的信息(顶点1顶点2权值)";
charci,cj;
inti=-1,j=-1;
cin>>ci>>cj>>cost;//读入边
//将输入的节点名(A,B,C...)转化成部的下标
i=ci-'A';
j=cj-'A';
//将输入的vi-vj这条边插入到邻接表头部
s=(EdgeNode*)malloc(sizeof(EdgeNode));
s->src=i;
s->srcName=G->adjlist[i].vertex;
s->adjvex=j;
s->adjName=G->adjlist[j].vertex;
s->cost=cost;
s->next=G->adjlist[i].firstedge;//插入表头
G->adjlist[i].firstedge=s;
s=(EdgeNode*)malloc(sizeof(EdgeNode));
s->src=j;
s->srcName=G->adjlist[j].vertex;
s->adjvex=i;
s->adjName=G->adjlist[i].vertex;
s->cost=cost;
s->next=G->adjlist[j].firstedge;
G->adjlist[j].firstedge=s;
}
}
3.用普利姆算法生成最小生成树
intisExists(int*visited,intn,intvex)//判断vex是否在visited数组里
{
intexists=0;
for(inti=0;i{
if(visited[i]==vex)
{
exists=1;
}
}
returnexists;
}
voidprime(ALGraph*G,intfrom)//用普利姆算法求最小生成树
{
intvisitedNodes[MaxVertexNum];
intvisitedIndex=0;
visitedNodes[visitedIndex++]=from;
EdgeNodechosen[MaxEdgeNum];
intedgeIndex=0;
floattotalMinCost=0;
while(visitedIndex!
=G->n)//当访问到所有的点,就表示整个过程完毕
{
EdgeNode*minEdge=NULL;
floatminCost=9999;
for(inti=0;i{
EdgeNode*p=G->adjlist[visitedNodes[i]].firstedge;
while(p!
=NULL)
{
if(isExists(visitedNodes,visitedIndex,p->adjvex)==0&&p->cost{
minCost=p->cost;
minEdge=p;
}
p=p->next;
}
}
totalMinCost+=minCost;
chosen[edgeIndex++]=*minEdge;
cout<srcName<<"->"<adjName<visitedNodes[visitedIndex++]=minEdge->adjvex;
}
}
4.主函数
intmain()
{
printf("试验名称:
管道铺设施工的最正确方案问题\n");
printf("学号:
031350103\n");
printf(":
\n");
printf("=========================================================\n");
time_trawtime1;
structtm*timeinfo1;
time(&rawtime1);
timeinfo1=localtime(&rawtime1);//时间函数;
printf("程序运行开始,当前日期和时间:
%s",asctime(timeinfo1));
ALGraph*G=(ALGraph*)malloc(sizeof(ALGraph));
create(G);
cout<<"建立的图邻接表表示为:
"<for(inti=0;in;i++)
{
EdgeNode*p=G->adjlist[i].firstedge;
printf("%d->",i);//输出建立的邻接表
while(p!
=NULL)
{
printf("%d->",p->adjvex);
p=p->next;
}
printf("\n");
}
printf("应用prim算法,得到的最小生成树是:
");
prime(G,0);
charkong;
cin>>kong;//输出最小生成树
return0;
time_trawtime2;
structtm*timeinfo2;
time(&rawtime2);
timeinfo2=localtime(&rawtime2);
printf("程序运行完毕,当前日期和时间:
%s",asctime(timeinfo2));
}
五、调试分析
1、程序将小区的相关信息输入存储在图的邻接表结构中,每个节点与小区一一对应,权值与小区之间的距离一一对应,只需要输入节点符号,以与相应的权值,程序会自动输出相应的最小生成树即相应的管道铺设线路。
2、算法的时空分析:
(1)由于create(ALGraph*G)程序中读入顶点的操作执行了n次,读入边的操作执行了e次,故其时间复杂度为O(n+2e)
(2)prime(ALGraph*G,intfrom)的时间复杂度为O(n^2),n是顶点个数;
(3)所有算法的空间复杂度都是O
(1).
六、使用说明
用户首先根据提示输入节点数n和边数e,应输入整数,用空格隔开,如:
915;
再根据提示输入n个结点的名称,分n次输入;
再根据提示输入边的信息,即两个端点的名称与该边的权值,名称为字符,权值为实数,用空格隔开,如:
AB32.8,分e次输入
输入完成后不需操作,自动输出所建立的邻接表与最小生成树的结果
七、调试结果
输入节点数边数:
915
输入九个结点的名称:
ABCDEFGHI
输入边的信息,即两个端点的名称与该边的权值:
(AB32.8);(BC5.9);(CD21.3);(DE67.3);
(AC44.6);(AH12.1);(AI18.2);(HI8.7);(HG52.5);(CG56.4);(CE41.1);(EF85.6);
(DF98.7);(IF79.2);(EG10.5)
输入完毕直接输出“建立的图邻接表表示为:
0->8->7->2->1->2->0->2->4->6->0->3->1->3->5->4->2->4->6->5->2->3->5->8->3->4->6->4->2->7->7->6->8->0->8->5->7->0”
输出“应用prim算法,得到的最小生成树是:
A->H
H->IA->BB->CC->DC->EE->GI->F”
初始界面为:
输入数据时的界面:
输出界面:
八、遇到的问题和解决方法:
1.最初拿到这个题目时还不会普利姆算法的具体容,只知道求最小生成树的两个方法叫普利姆算法和克里斯卡尔算法,但不理解也不会写代码。
于是我上网查阅了相关资料,还请教了上机时给我们辅导的研究生学长,学会了prim算法。
2.开始建立邻接表的时候我是照着《软件技术基础教程》课本上给的邻接表存储有向图的代码修改的,想让它存储无向图,但开始只是在创建边表结点时设置了两个char型变量存放两个名称和两个int型变量存储序号,后面不知道怎么改,后经助教学长指点知create(ALGraph*G)中对应改动,将新表结点插入到vi的边表头部这里的操作是双向的才能保证图是无向的,即,插入到vi后一次,插入到vj后一次,如这段代码所示
s->src=i;
s->next=G->adjlist[i].firstedge;//插入表头
G->adjlist[i].firstedge=s;
s->src=j;
s->next=G->adjlist[j].firstedge;
G->adjlist[j].firstedge=s;
3.输入所有的结点和边的信息后程序运行出错,如图:
后经排查调试发现错误原因是:
在输出图G的时候,直接用G->adjlist[i].firstedge这个指针,并在输出的过程中,不断的修改G->adjlist[i].firstedge,导致firstedge最后被修改成了NULL,在后面的Prime算法中出现了空指针异常。
修改方法是,用指针p代替G->adjlist[i].firstedge做遍历,防止了G->adjlist[i].firstedge被随意修改。
经再测试发现运行正常,错误得到解决。
九、实验收获和感想:
这次的计算机实践题目是要求用邻接表存储无向图再求出最小生成树,完成以后感觉这一次的程序是本学期计算机实践数据结构部分相对较难的一个题目。
我们在课本上给出的程序语句样例是建立有向图,建立无向图时只需要做以修改,在边表结点中设置两组变量分别存储两端的节点。
这个程序只需要求最小生成树,而且题目说明了要用邻接表存储,即需求明确且不复杂,所以设计程序成思路明确,先建立邻接表再求最小生成树。
再求最小生成树时,有普里姆算法和克里斯卡尔算法两种选择,我选择了自己更为理解的普里姆算法。
这也是第一次运用这些只理解理论的算法来写实际的程序。
写过调试过才对算法的精髓有了深入的理解。
完成整个程序设计使得对数据结构、算法的使用更加熟练。
同时通过直接对图的操作,加深了对数据结构的理解和认识。
感觉自己编写程序的能力在一次次实践中有着显著的进步,要想真正理解并记住一个算法,亲自的编写程序比其他任何方法都更加有效果。
比如本次编程前我对于普里姆算法完全不懂,只知道它是用来求解最小生成树的,却没有想过它的逻辑思路,知道这次要用到才去查找资料学习普里姆算法,最终在运用中实现了从不会到熟练运用的转型。
感觉收获非常大。
以后即使这门实践课完毕了,我也要经常联系编写程序,在实践运用中学习算法。
十、源程序
#include
#include
#include
#include
#include
#defineMaxVertexNum50
#defineMaxEdgeNum1000//边的最大值
typedefstructnode//边表节点
{
intsrc;//边端的序号
charsrcName;//边端的名称
intadjvex;//邻接点域
node*next;//指向下一个邻接点的指针域
charadjName;
floatcost;//边的权值
}EdgeNode;
typedefstruct//顶点表节点
{
charvertex;//顶点域
EdgeNode*firstedge;//边表头指针
}VertexNode;
typedefVertexNodeAdjList[MaxVertexNum];//AdjList是邻接表类型
typedefstruct
{
AdjListadjlist;//邻接表
intn,e;//顶点数和边数
}ALGraph;//ALGraph是以邻接表方式存储的图类型
voidcreate(ALGraph*G)//建立无向图的邻接表存储
{
intk,w,v;
EdgeNode*s;
cout<<"请输入节点数和边数(用空格隔开)"<cin>>G->n>>G->e;//读入顶点数和边数
for(inti=0;in;i++)//建立有n个顶点的顶点表
{
cout<<"请输入顶点名称:
";
charc;
cin>>c;//读入顶点信息
G->adjlist[i].vertex=c;
G->adjlist[i].firstedge=NULL;//顶点表的边表头指针设为空
}
printf("建立边表\n");
for(k=0;ke;k++)//建立边表
{
floatcost;
cout<<"请输入边的信息(顶点1顶点2权值)";
charci,cj;
inti=-1,j=-1;
cin>>ci>>cj>>cost;//读入边
i=ci-'A';//将输入的节点名(A,B,C...)转化成部的下标
j=cj-'A';
s=(EdgeNode*)malloc(sizeof(EdgeNode));//将输入的vi-vj这条边插入到邻接表头部s->src=i;
s->srcName=G->adjlist[i].vertex;
s->adjvex=j;
s->adjName=G->adjlist[j].vertex;
s->cost=cost;
s->next=G->adjlist[i].firstedge;//插入表头
G->adjlist[i].firstedge=s;
s=(EdgeNode*)malloc(sizeof(EdgeNode));
s->src=j;
s->srcName=G->adjlist[j].vertex;
s->adjvex=i;
s->adjName=G->adjlist[i].vertex;
s->cost=cost;
s->next=G->adjlist[j].firstedge;
G->adjlist[j].firstedge=s;
}
}
intisExists(int*visited,intn,intvex)//判断vex是否在visited数组里
{
intexists=0;
for(inti=0;i{
if(visited[i]==vex)
{
exists=1;
}
}
returnexists;
}
voidprime(ALGraph*G,intfrom)//用普利姆算法求最小生成树
{
intvisitedNodes[MaxVertexNum];
intvisitedIndex=0;
visitedNodes[visitedIndex++]=from;
EdgeN