相似三角形常见模型总结.docx

相似三角形常见模型总结.docx

《相似三角形常见模型总结.docx》由会员分享，可在线阅读，更多相关《相似三角形常见模型总结.docx（7页珍藏版）》请在冰豆网上搜索。

相似三角形常见模型总结

相似三角形常见模型总结

模型一　利用“标杆”测高

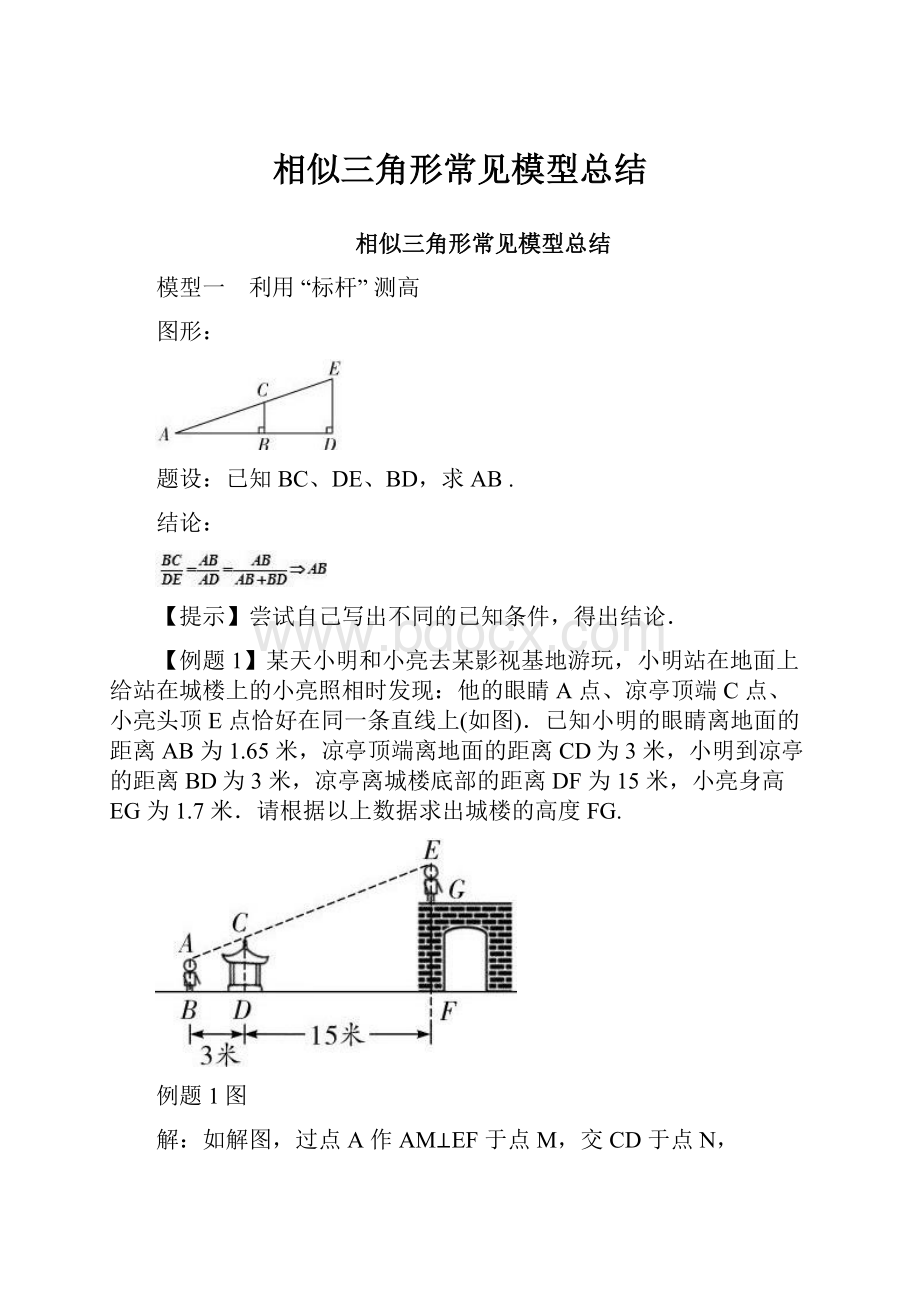
图形：

题设：

已知BC、DE、BD，求AB.

结论：

【提示】尝试自己写出不同的已知条件，得出结论．

【例题1】某天小明和小亮去某影视基地游玩，小明站在地面上给站在城楼上的小亮照相时发现：

他的眼睛A点、凉亭顶端C点、小亮头顶E点恰好在同一条直线上（如图）．已知小明的眼睛离地面的距离AB为1.65米，凉亭顶端离地面的距离CD为3米，小明到凉亭的距离BD为3米，凉亭离城楼底部的距离DF为15米，小亮身高EG为1.7米．请根据以上数据求出城楼的高度FG.

例题1图

解：

如解图，过点A作AM⊥EF于点M，交CD于点N，

例题1解图

由题意可得，AN＝3米，CN＝3－1.65＝1.35（米），MN＝15米，

∵CN∥EM，

∴△ACN∽△AEM，

∴CN/EM=AN/AM,

∴1.35/EM=3/18,

解得EM＝8.1，

∵AB＝MF＝1.65米，

∴城楼的高度FG为8.1＋1.65－1.7＝8.05（米），

答：

城楼的高度FG为8.05米．

模型二　中心投影

图形：

题设：

结论：

【提示】尝试自己写出不同的已知条件，得出结论．

【例题2】如图，在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时，在路灯C的照射下小明的影长正好为NB，在路灯A的照射下小明的影长NE为2m，求小明离路灯CD的距离．

例题2图

解：

∵MN⊥BD，AB⊥BD，CD⊥BD，

∴△EMN∽△EAB，△BMN∽△BCD，

∵AB＝CD，BD＝24m，NE＝2m，

∴BN＝6m（负值舍去），

∴ND＝24－6＝18（m）.

答：

小明离路灯CD的距离为18m.

模型三　平行投影

图形：

题设：

结论：

【提示】尝试自己写出不同的已知条件，得出结论．

【例题3】如图，在阳光下，某一时刻，旗杆AB的影子一部分在地面上，另一部分在建筑物的墙面上．小明测得旗杆AB在地面上的影长BC为20m，在墙面上的影长CD为4m，同一时刻，小明又测得竖立于地面长1m的标杆的影长为0.8m，求旗杆的高度AB.

例题3图

解：

如解图，作DE⊥AB于点E，

例题3解图

∵DC⊥BC于点C，AB⊥BC于点B，

∴四边形BCDE为矩形，

∴DE＝BC＝20m，BE＝DC＝4m，

∵同一时刻物高与影长所组成的三角形相似，

∴1/0.8=AE/20,

解得AE＝25m，

∴AB＝25＋4＝29（m）．

答：

旗杆的高度AB为29m.

模型四　镜面反射、倒影

图形：

题设：

结论：

【提示】尝试自己写出不同的已知条件，得出结论．

【例题4】如图，要测量河两岸相对的两点A、B的距离，先从B处出发沿与AB成90°角方向，向前走80米到C处立一标杆，然后方向不变向前走50米至D处，在D处转90°，沿DE方向走30米，到E处，使点A、C与E在同一条直线上，则A、B间的距离是多少？

例题4图

解：

∵∠B＝90°，DE⊥BD，

∴AB∥DE，

∴△ACB∽△ECD，

∴AB/ED=BC/DC,

∴AB/30=80/50,

∴AB=80×30÷50=48（米）.

答：

A、B间的距离是48米．

模型五　固定视角

图形：

题设：

结论：

【提示】尝试自己写出不同的已知条件，得出结论．

【例题5】如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE＝0.4m，EF＝0.2m，测得边DF离地面的高度AC＝1.5m，CD＝8m，求树高．

例题5图

解：

∵∠DEF＝∠DCB＝90°，∠D＝∠D，

∴△DEF∽△DCB，

∴DE/DC=EF/CB,

∵DE＝0.4m，EF＝0.2m，CD＝8m，

∴0.4/8=0.2/BC,

∴CB＝4m，

∴AB＝AC＋BC＝1.5＋4＝5.5（m）．

答：

树高为5.5m.