卧式储罐不同液位下的容积计算.docx
《卧式储罐不同液位下的容积计算.docx》由会员分享,可在线阅读,更多相关《卧式储罐不同液位下的容积计算.docx(9页珍藏版)》请在冰豆网上搜索。
卧式储罐不同液位下的容积计算
卧式储罐不同液位容积(质量)计算
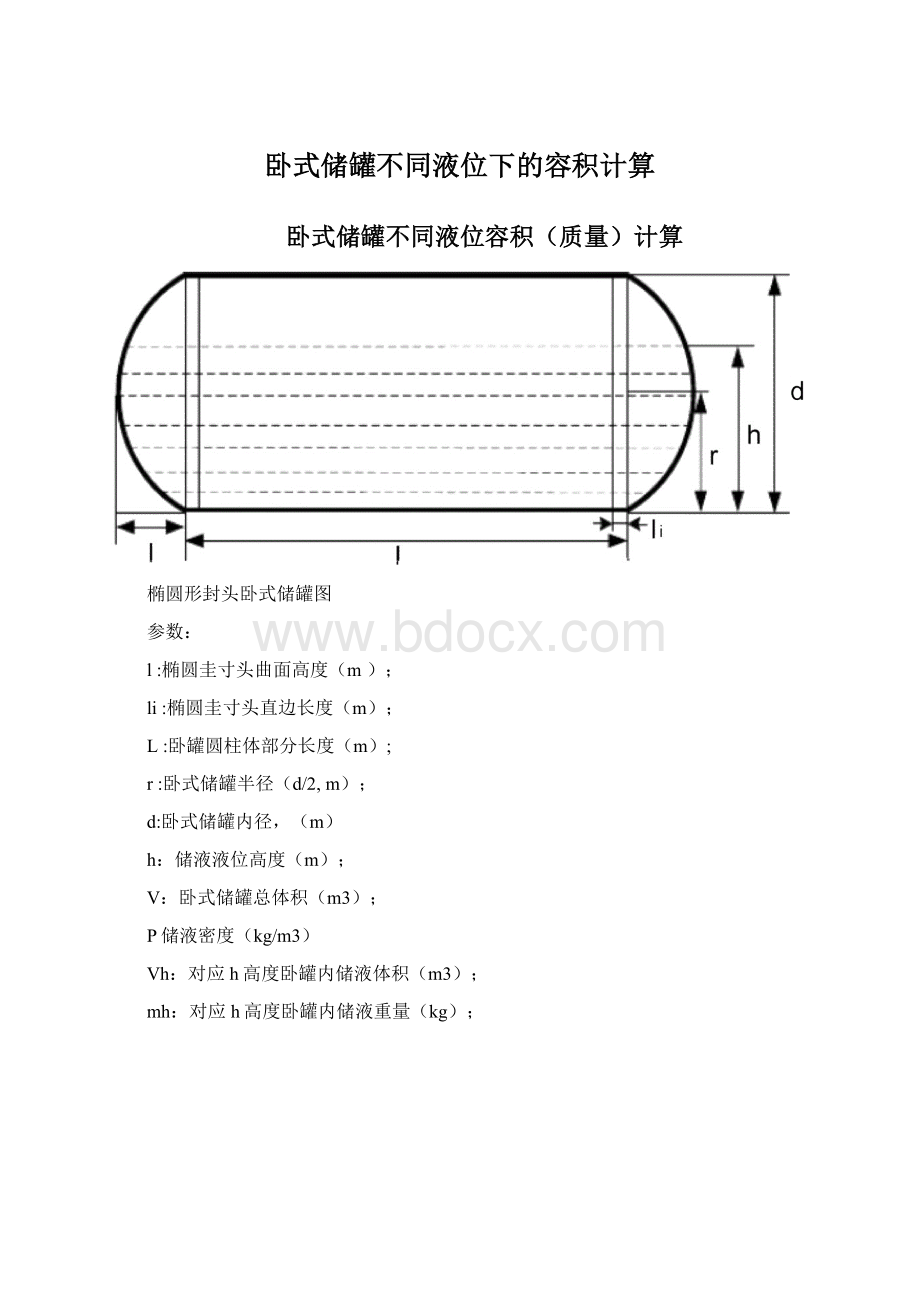
椭圆形封头卧式储罐图
参数:
l:
椭圆圭寸头曲面高度(m);
li:
椭圆圭寸头直边长度(m);
L:
卧罐圆柱体部分长度(m);
r:
卧式储罐半径(d/2,m);
d:
卧式储罐内径,(m)
h:
储液液位高度(m);
V:
卧式储罐总体积(m3);
P储液密度(kg/m3)
Vh:
对应h高度卧罐内储液体积(m3);
mh:
对应h高度卧罐内储液重量(kg);
椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧
封头可组成椭圆球体。
简化模型图如下
卧式储罐内储液总体积计算公式:
若密度为p,则卧式储罐内储液总重量为:
mhVh
表1卧式储罐不同液位下容积(重量)
P
r
L
h
Vh
mh
液体密度
(kg/m3)
储罐半径
(m)
圆柱体部分长度
(m)
储液液位高度
(m)
储液体积
(m3)
储液重量
(kg)
备注:
该计算公式推导过程如下
卧式储罐不同液位下的容积简化计算公
椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧
封头可组成椭圆球体。
(1)椭圆球体部分
该椭圆球体符合椭圆球体公式:
222222务告务1其中a=b=r,则有x2务1abcac
垂直于y轴分成无限小微元,任一微元面积为:
Syi—(a2y2)
a
当液面高度为h时,椭圆球体内液氨容积为
h「3o3
V1=aSyjdya^(a2y2)dy許2h自
(2)直段筒体部分:
筒体的纵断面方程为x2y2a2
任一微元的面积为Syj2、.、a2y2dy
则筒体部分容积为:
L2a2y2dyLa2(arcsin」
aa
(arcsin-)
2a2
(3)卧式储罐储液总体积
总容积为V二V1+V2,
232
c2-4h2a2(.hhr.2、
V=(ah)+La(arcsin2;ah)
a33aa2
此公式中液位高度h是以储罐内径中心为原点,其中a=b=r
化简后卧式储罐储液总体积为:
2
实例:
某热电厂液氨罐尺寸为:
储罐体积50m3,直段筒体长度Li=8480mm,
封头直段长度L2=40mm(圆柱体部分长度为(Li+L2/2)=8580mm),筒体半径
R=a=b=1300mm,圭寸头高度c=650mm
p
V
r
l
L
h
h尺
Vh
mh
误
液体密度
(kg/m3)
储罐总体积
(m)
储罐半径
(m
封头高度
(m
圆柱体部分长度(m
储液液位高度(中点为坐标原点)
(m
实际标尺
刻度
储液体积
(m)
储液重量
(kg)
不同液咼下计算得到的体积与实际储液体积间
误
1
50
1.3
0.65
8.58
-1.3
0
0.000
0.000
0.00%
1
50
1.3
0.65
8.58
-0.975
0.325
3.619
3.619
1
50
1.3
0.65
8.58
0
1.3
25.078
25.078
0.31%
1
50
1.3
0.65
8.58
0.975
2.275
46.537
46.537
1
50
1.3
0.65
8.58
1.3
2.6
50.155
50.155
0.31%
若液位高度h以卧罐底部为起点,如下图
/
\A/
\r
f1
f
\y
丿
1二;
o
h\
J
V
7
\…一j
J
■厶■NKA*
则卧式储罐内储液总体积计算公式:
若密度为p,则卧式储罐内储液总重量为:
mhVh
p
r
L
h
Vh
mh
液体密度
储罐半径
圆柱体部分长度
储液液位高度
储液体积
储液重量(kg)
(kg/m3)
(m)
(m)
(m)
(m3)
1
1.3
8.58
0.325
3.619
3.619
1
1.3
8.58
1.3
25.078
25.078
1
1.3
8.58
2.275
46.537
46.537
其它方法如下:
第一种方法
|PDF.
卧式储罐不同液位下的容积简化计算公
卧式储罐内储液总体积计算公式:
VhV
(hr)2Kr
2l(hr)[1」宀]L[(hr)「2hrh2r2arcsin()]
3rr
若密度为p,则卧式储罐内储液总重量为:
mhVh
P
V
r
l
L
h
Vh
mh
误
液体密度
(kg/m3)
储罐总体积
(m3)
储罐半径
(m)
封头高度
(m)
圆柱体
部分长度(m)
储液液位高
度(m)
储液体积
(m3)
储液重量
(kg)
不同液咼下计算得到的体积与实际储液体积间误差
1
50
1.3
0.65
8.58
0
-1.315
出现负数,不复合实际
1
50
1.3
0.65
8.58
0.325
2.276
2.276
1
50
1.3
0.65
8.58
1.3
25.000
25.000
0.00%
1
50
1.3
0.65
8.58
2.275
47.724
47.724
1
50
1.3
0.65
8.58
2.6
51.315
2.63%
此方式用到参数较多P、V、r、l、L、h。
当液高为0时理论上液体体积应为0,此公式结果为负值,不合逻辑。
第二种方法
卧式储罐内储液总体积计算公式:
JdhL(対E
若密度为p,则卧式储罐内储液总重量为:
mhVh
P
V
d
l
L
h
Vh
mh
液体密度
(kg/m3)
储罐总体积
(m3)
储罐直径
(m)
封头高度
(m)
圆柱体部分长度(m)
储液液位高
度(m)
储液体积
(m3)
储液重量
(kg)
不同液咼下计算得到的体积与实际储液体积间误差
1
50
2.6
0.65
8.58
0
#DIV/0!
1
50
2.6
0.65
8.58
0.325
3.786
3.786
1
50
2.6
0.65
8.58
1.3
24.109
24.109
-3.56%
1
50
2.6
0.65
8.58
2.275
52.255
52.255
1
50
2.6
0.65
8.58
2.6
#DIV/0!
此公式是由体积公式推算的,相对误差较大,如储罐中储液在一般高度时,体积间误差偏大。
此外,由于公式中存在分数,液高为0和最大公式
不适用。
三种方法对比详见excel表格。