磁场习题带答案.docx
《磁场习题带答案.docx》由会员分享,可在线阅读,更多相关《磁场习题带答案.docx(20页珍藏版)》请在冰豆网上搜索。
磁场习题带答案
磁场
一、选择题(本题共10小题,每小题4分,在每小题给出的四个选项中,有多项符合题目要求的,全部选对的得4分,选对但不全的得2分,有选错的得0分)
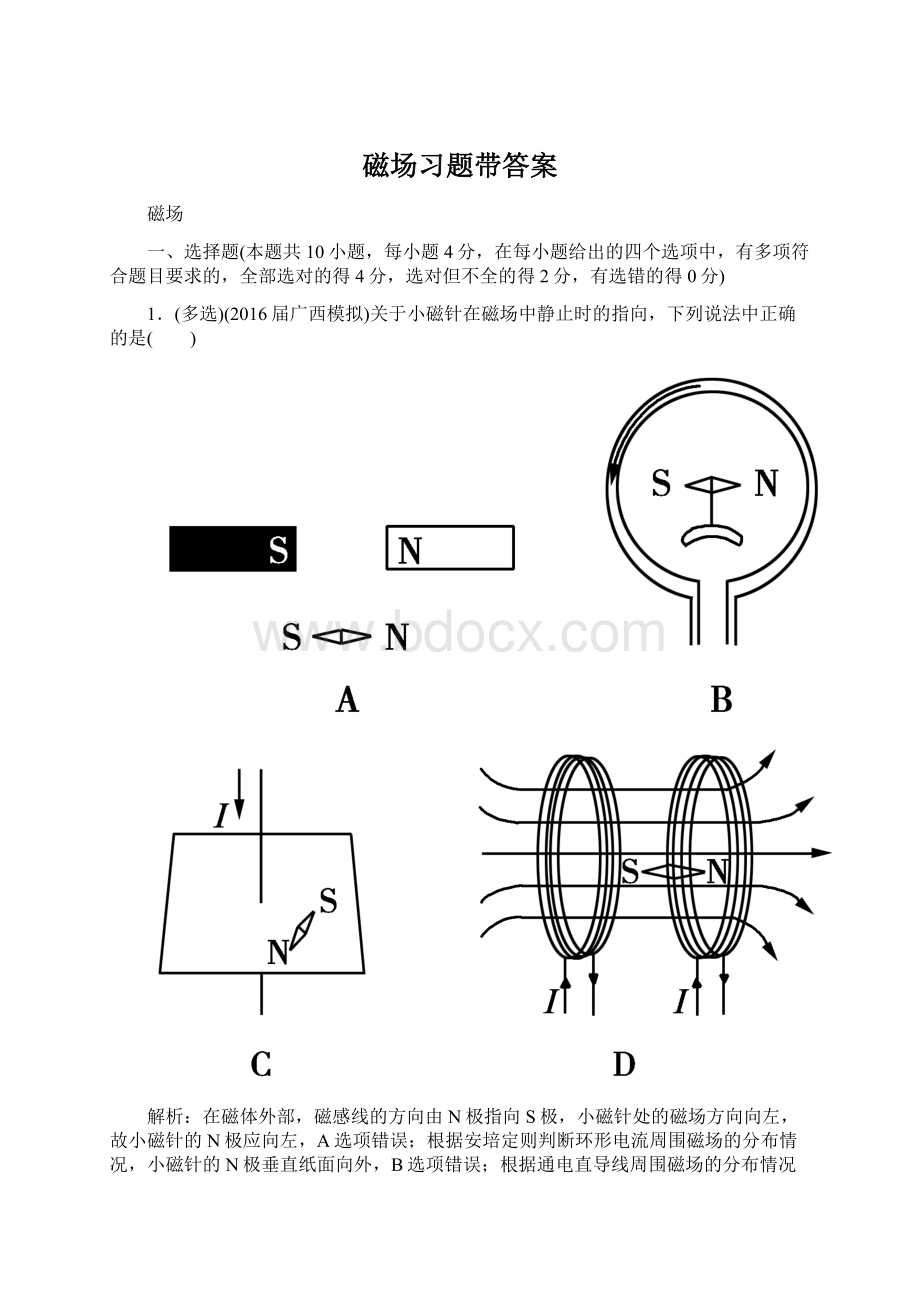
1.(多选)(2016届广西模拟)关于小磁针在磁场中静止时的指向,下列说法中正确的是( )
解析:
在磁体外部,磁感线的方向由N极指向S极,小磁针处的磁场方向向左,故小磁针的N极应向左,A选项错误;根据安培定则判断环形电流周围磁场的分布情况,小磁针的N极垂直纸面向外,B选项错误;根据通电直导线周围磁场的分布情况可知,小磁针在磁场中静止时的指向是正确的,C选项正确;小磁针所在位置的磁场水平向右,则N极指向右,D选项正确.
答案:
CD
2.(2016届洛阳模拟)如图所示,一个静止的质量为m、带电荷量为q的粒子(不计重力),经电压U加速后垂直进入磁感应强度为B的匀强磁场,粒子在磁场中转半个圈后打在P点,设OP=x,能够正确反应x与U之间的函数关系的是( )
解析:
粒子在电场中加速运动,qU=mv2-0,在磁场中做匀速圆周运动,洛伦兹力提供向心力,qvB=m,其中x=2R,联立解得,x=·,分析可知x�U图象是抛物线,B选项正确.
答案:
B
3.(2016届广东省东莞市联考)如图所示,半径为R的圆形区域内有垂直于纸面向里的匀强磁场.重力不计、电荷量一定的带电粒子以速度v正对着圆心O射入磁场,若粒子射入、射出磁场点间的距离为R,则粒子在磁场中的运动时间为( )
A. B. C. D.
解析:
分析题意,画出轨迹图如图:
根据几何关系可知,轨迹半径r=R,运动周期T=,轨迹对应的圆心角为π,粒子在磁场中的运动时间t=·=,A选项正确.
答案:
A
4.(2016届辽宁省鞍山市二模)回旋加速器是获得高能量带电粒子的装置,其核心部分是分别与高频交流电源的两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法中正确的是( )
A.加速电压越大,带电粒子从D形盒射出时的动能越大
B.带电粒子从D形盒射出时动能与磁场的强弱无关
C.交变电场的周期应为带电粒子做圆周运动周期的二倍
D.用同一回旋加速器分别加速不同的带电粒子,一般要调节交变电场的频率
解析:
根据回旋加速器的工作原理可知,带电粒子射出D形盒的动能Ek=,与磁场的强弱有关,与加速电压无关,A、B选项错误;交变电场的周期与带电粒子圆周运动的周期相等,C选项错误;带电粒子运动的周期T=,粒子不同,周期不同,频率不同,分别加速不同的带电粒子,一般要调节交变电场的频率,D选项正确.
答案:
D
5.(2016届辽宁省本溪市二模)如图所示,等腰直角三角形abc区域中有垂直纸面向里的匀强磁场B,速度为v0的带电粒子,从a点沿ab方向射入磁场后恰能从c点射出,现将匀强磁场B换成垂直ac边向上的匀强电场E,其它条件不变,结果粒子仍能从c点射出,粒子的重力不计,则下列说法中正确的是( )
A.粒子带正电
B.=
C.粒子从磁场中离开时的速度方向与从电场中离开时的速度方向不同
D.粒子从磁场中离开时的速度大小与从电场中离开时的速度大小不同
解析:
粒子在磁场中做匀速圆周运动,轨迹如图所示:
设ab=L,根据几何关系可知,轨道半径r=L,根据左手定则可知,粒子带负电,A选项错误;洛伦兹力提供向心力,qv0B=m,解得,B=,粒子在电场中做类似斜抛运动,竖直方向上,y=v0t-t2=0,水平方向上,x=L=v0t,联立解得,E=,故=,B选项正确;在磁场中离开c点的速度方向沿着bc方向,在电场中离开c点的速度方向也是沿着bc方向,C选项错误;在磁场中,洛伦兹力不做功,离开c点的速度等于初速度,在电场中,a点与c点是等势点,电场力不做功,离开c点的速度也等于初速度,D选项错误.
答案:
B
6.(多选)(2016届辽宁省本溪市一模)如图所示,一电荷量为q,质量为m的带正电粒子,经过水平方向的加速电场U1,沿水平方向进入竖直方向的偏转电场U2,已知粒子从偏转电场下极板最左端的G点进入,恰从上极板最右端A点离开偏转电场,立即垂直射入一圆形区域的匀强磁场内,AC是圆形磁场区域的一条沿水平方向的直径.粒子速度方向与AC成α=15°,已知圆形区域的直径为D、磁感应强度为B,磁场方向垂直于圆平面指向外,tan15°=2-,若此粒子在磁场区域运动过程中,速度的方向一共改变了90°,重力忽略不计,则下列说法正确的是( )
A.粒子在磁场中运动速度大小为
B.该粒子在磁场中运动的时间为
C.偏转电场的板间距d和板长L的比值d∶L=2∶(2+)
D.加速电场和偏转电场所加电压比U1∶U2=(7+4)∶1
解析:
画出轨迹如图所示:
根据几何关系可知,∠CAE=30°,AE=Dcos∠CAE=D,则轨迹半径r=AE=D,洛伦兹力提供向心力,qvB=m,解得v=,A选项正确;粒子运动时间t=,B选项正确;粒子在偏转电场中做类平抛运动,竖直方向上,d=t,水平方向上,L=vxt,其中tan15°=,联立解得,d∶L=1∶2(2+),C选项错误;粒子在加速电场中,qU1=mv-0,偏转电场中,qU2=m()2-mv,联立解得,U1∶U2=(7+4)∶1,D选项正确.
答案:
ABD
7.(多选)(2016届江西新余期中)如图所示,足够长的光滑三角形绝缘槽,与水平面的夹角分别为α和β(α>β),加垂直于纸面向里的磁场.分别将质量相等、带等量正、负电荷的小球a、b依次从两斜面的顶端由静止释放,关于两球在槽上运动的说法正确的是( )
A.在槽上,a、b两球都做匀加速直线运动,且加速度aa>ab
B.a、b两球沿槽运动的最大速度为va和vb,则va>vb
C.a、b两球沿直槽运动的最大位移为xa和xb,则xa<xb
D.a、b两球沿槽运动的时间为ta和tb,则ta<tb
解析:
根据左手定则可知,两小球受到的洛伦兹力垂直斜面向上,在槽上运动时,加速度aa=gsinα,ab=gsinβ,即aa>ab,A选项正确;当洛伦兹力与重力沿垂直斜面向下分力相等时,小球脱离斜面,Bqva=mgcosα,Bqvb=mgcosβ,解得,va=,vb=,α>β,则va<vb,B选项错误;根据运动学公式得,v=2gsinα·xa,v=2gsinβ·xb,解得xa<xb,C选项正确;va=gsinα·ta,vb=gsinβ·tb,解得ta=,tb=,则ta<tb,D选项正确.
答案:
ACD
8.(2016届江西南昌模拟)如图所示,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直.在电磁场区域中,有一个固定在竖直平面内的光滑绝缘圆环,环上套有一个带正电的小球.O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,bO沿水平方向.已知小球所受电场力与重力大小相等.现将小球从环的顶端a点由静止释放,下列判断正确的是( )
A.当小球运动到b点时,小球受到的洛伦兹力最大
B.当小球运动到c点时,小球受到的支持力一定大于重力
C.小球从a点运动到b点,重力势能减小,电势能增大
D.小球从b点运动到c点,电势能增大,动能先增大后减小
解析:
已知小球所受的电场力与重力大小相等,合力指向bc圆弧的中点,小球从a点释放,运动到bc圆弧的中点时,合力做功最多,根据动能定理可知,动能最大,小球受到的洛伦兹力最大,A选项错误;小球运动到c点时,由支持力、洛伦兹力和重力的合力提供向心力,FN+F洛-mg=m,FN不一定大于mg,B选项错误;小球从a点运动到b点,重力和电场力均做正功,重力势能和电势能均减小,C选项错误;小球从b点运动到c点,电场力做负功,电势能增大,合力先做正功后做负功,动能先增大后减小,D选项正确.
答案:
D
9.(2016届四川南充市期中)如图所示的虚线区域内,充满垂直于纸面向里的匀强磁场和竖直向下的匀强电场.一带电粒子a(不计重力)以一定的初速度由左边界的O点射入磁场、电场区域,恰好沿直线由区域右边界的O′(图中未标出)穿出.若撤去该区域内的磁场而保留电场不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b( )
A.穿出位置一定在O′点下方
B.穿出位置一定在O′点上方
C.运动时,在电场中的电势能一定减小
D.在电场中运动时,动能一定减小
解析:
a粒子在电场和磁场的复合场区内做匀速直线运动,Bqv=Eq,解得E=Bv,无论粒子带正电还是负电,粒子都可以沿直线穿出复合场区,当撤去磁场只保留电场时,粒子b由于电性不确定,故无法判断从O′点的上方或下方穿出,A、B选项错误;粒子b在穿过电场区的过程中受到电场力的作用,电场力做正功,电势能减小,动能增大,C选项正确,D选项错误.
答案:
C
10.(多选)(2016届河南模拟)如图所示,水平放置的光滑平行金属导轨,左端通过开关S与内阻不计、电动势为E的电源相连,右端与半径为L=20cm的光滑圆弧导轨相接.导轨宽度为20cm,电阻不计.导轨所在空间有竖直方向的匀强磁场,磁感应强度B=0.5T.一根导体棒ab垂直导轨放置,质量m=60g、电阻R=1Ω,长也为20cm的绝缘细线悬挂,导体棒恰好与导轨接触.当闭合开关S后,导体棒沿圆弧摆动,摆动过程中导体棒始终与导轨接触良好且细线处于张紧状态.导体棒ab速度最大时,细线与竖直方向的夹角θ=53°(sin53°=0.8,g=10m/s2),则( )
A.磁场方向一定竖直向上
B.电源的电动势E=8.0V
C.导体棒在摆动过程中所受安培力F=8N
D.导体棒摆动过程中的最大动能为0.08J
解析:
当开关S闭合时,导体棒受到水平向右的安培力,向右摆动,根据左手定则可知,磁场方向竖直向下,A选项错误;安培力F=BIL=BL,导体棒ab速度最大时,细线与竖直方向的夹角θ=53°则tanθ=,解得E=8.0V,F=0.8N,B选项正确,C选项错误;根据动能定理得,FLsin53°-mgL(1-cos53°)=Ek-0,解得Ek=0.08J,D选项正确.
答案:
BD
第Ⅱ卷(非选择题,共60分)
二、计算题(本题共5小题,共60分)
11.(12分)(2016届常州模拟)如图所示,在磁感应强度为B、足够大的水平匀强磁场中,有两块长为2L,间距为d的竖直放置的平行带电金属板,从CD板的正中央O点由静止释放一个初速度为零的电子,电子恰好从AB板的边缘A端平行于AB板射出,且能回到O点.已知电子的电荷量为e,质量为m,重力可忽略不计,电场只局限于平行板之间,且L>d.试求:
(1)电子从板间射出时的速度大小;
(2)两板间所加电压;
(3)电子在复合场区域运动到A点时的加速度大小.
解析:
(1)分析题意可知,电子离开A点后在磁场中做匀速圆周运动,轨迹如图所示:
根据几何关系得,r2=L2+(r-d)2,洛伦兹力提供向心力,evB=m,联立解得v=.
(2)电子由O运动到A处过程中,洛伦兹力不做功,根据动能定理得,eU=mv2,解得U=.
(3)在A点,电场力和洛伦兹力的合力提供加速度,由牛顿第二定律得,evB-e=ma,解得a=.
答案:
(1)
(2)
(3)
12.(12分)(2016届青海省联考)如图所示,在无限长的竖直边界AC和DE间,上、下部分分别充满方向垂直于ADEC平面向外的匀强磁场,上部分区域的磁感应强度大小为B0,OF为上、下磁场的水平分界线.质量为m、带电荷量为+q的粒子从AC边界上与O点相距为a的P点垂直于AC边界射入上方区域,经OF上的Q点第一次进入下方区域,Q与O点的距离为3a.不考虑粒子重力.
(1)求粒子射入时的速度大小;
(2)要使粒子不从AC边界飞出,求下方区域的磁感应强度应满足的条件;
(3)若下方区域的磁感应强度B=3B0,粒子最终垂直DE边界飞出,求边界DE与AC间距离的可能值.
解析:
(1)画出粒子运动的轨迹如图所示:
设粒子在OF上方做圆周运动半径为r,根据几何关系得,r2-(r-a)2=(3a)2,cosθ=,洛伦兹力提供向心力,qvB0=m,联立解得v=,cosθ=.
(2)粒子恰好不从AC边界飞出,画出轨迹如图所示:
设粒子在OF下方做圆周运动的半径为r1,根据几何关系得,r1+r1cosθ=3a,其中cosθ=,解得r1=,洛伦兹力提供向心力,qvB1=m,解得B1=,当B1>时,粒子不会从AC边界飞出.
(3)当B=3B0时,粒子最终垂直DE边界飞出,轨迹如图所示:
粒子在OF下方的运动半径为r2=a,设粒子的速度方向再次与射入磁场时的速度方向一致时的位置为P1,则P与P1的连线一定与OF平行,根据几何关系可知,PP1=4a,若粒子最终垂直DE边界飞出,边界DE与AC间的距离为L=nPP1=4na(n=123…).
答案:
(1)
(2)B1> (3)4na(n=123…)
13.(12分)(2016届温州十校联考)“太空粒子探测器”是由加速、偏转和收集三部分组成.其原理可简化如下:
如图所示,辐射状的加速电场区域边界为两个同心平行半圆弧面,圆心为M,外圆弧面AB与内圆弧面CD的电势差为U.图中偏转磁场分布在以P为圆心,半径为3R的圆周内,磁感应强度大小为B,方向垂直纸面向外;内有半径为R的圆盘(圆心在P处)作为收集粒子的装置,粒子碰到圆盘边缘即被吸收.假设太空中漂浮着质量为m,电荷量为q的带正电粒子,它们能均匀地吸附到AB圆弧面上,并被加速电场从静止开始加速,从M点以某一速率向右侧各个方向射入偏转磁场,不计粒子间的相互作用和其他星球对粒子引力的影响.
(1)粒子到达M点的速率?
(2)若电势差U=,则粒子从M点到达圆盘的最短时间是多少?
解析:
(1)设粒子到达M点的速度为v,根据动能定理得,qU=mv2-0,解得v=.
(2)
设粒子轨迹半径为r,洛伦兹力提供向心力,qvB=m,联立解得r=2R,若要时间最短,则粒子在磁场中运动的弦长最短,故从M斜向上射入,到达圆盘上的E点用时最短,如图所示:
根据几何关系可知,ME=EO=OM=2R,∠MOE=60°,解得tmin=T=.
答案:
(1)
(2)