初中几何最值问题.docx

初中几何最值问题.docx

《初中几何最值问题.docx》由会员分享，可在线阅读，更多相关《初中几何最值问题.docx（8页珍藏版）》请在冰豆网上搜索。

初中几何最值问题

初中几何最值问题

XX：

__________

指导：

__________

日期：

__________

几何最值问题大一统

追本溯源化繁为简

目有千万而纲为一，枝叶繁多而本为一。

纲举则目X，执本而末从。

如果只在细枝末节上下功夫，费了力气却讨不了好。

学习就是不断地归一，最终以一心一理贯通万事万物，则达自由无碍之化境矣（呵呵，这境界有点高，慢慢来）。

关于几何最值问题研究的老师很多，本人以前也有文章论述，本文在此基础上再次进行归纳总结，把各种知识、方法、思想、策略进行融合提炼、追本溯源、认祖归宗，以使解决此类问题时更加简单明晰。

一、基本图形

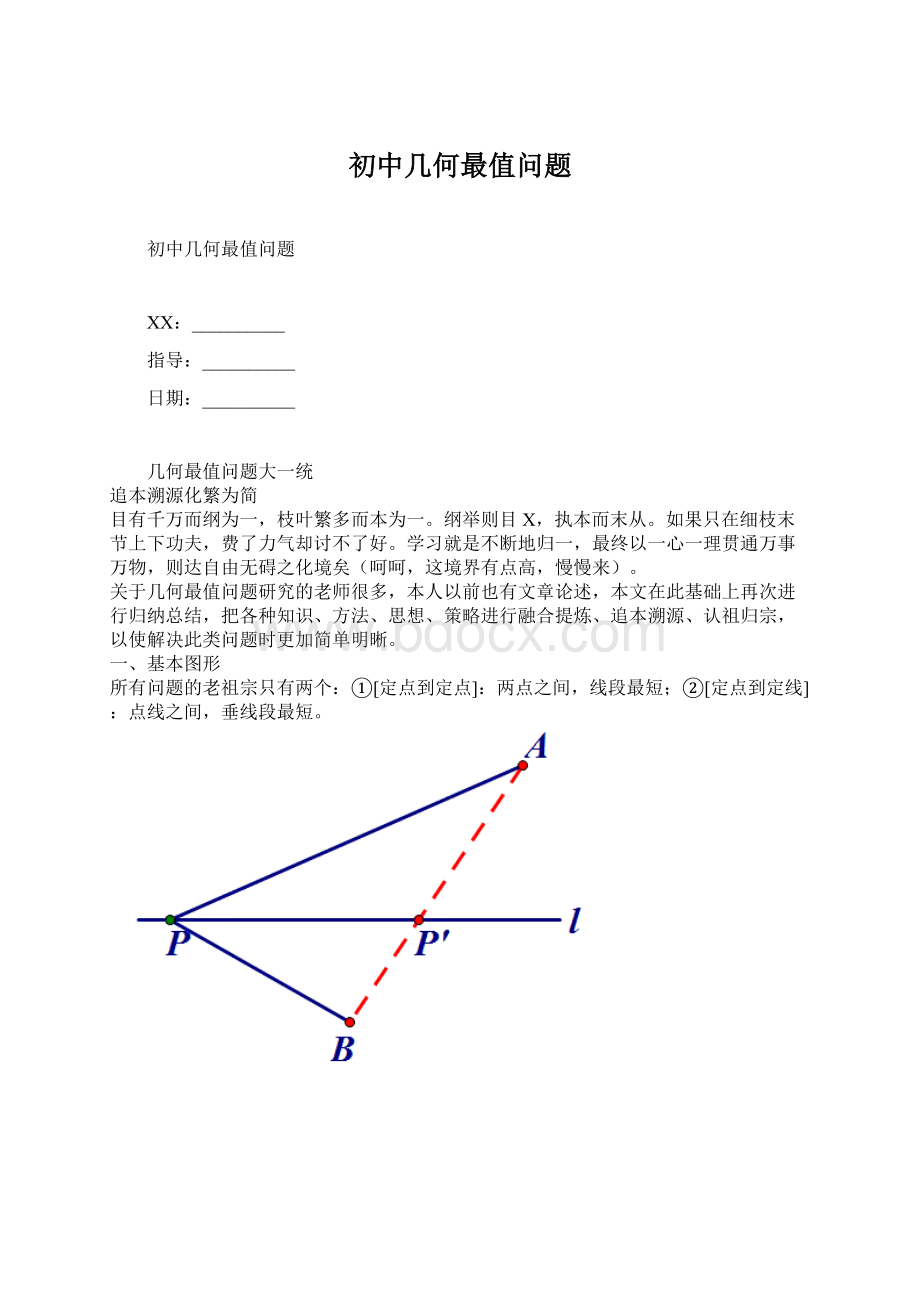
所有问题的老祖宗只有两个：

①[定点到定点]：

两点之间，线段最短；②[定点到定线]：

点线之间，垂线段最短。

由此派生：

③[定点到定点]：

三角形两边之和大于第三边；④[定线到定线]：

平行线之间，垂线段最短；⑤[定点到定圆]：

点圆之间，点心线截距最短（长）；⑥[定线到定圆]：

线圆之间，心垂线截距最短；⑦[定圆到定圆]：

圆圆之间，连心线截距最短（长）。

余不赘述，下面仅举一例证明：

[定点到定圆]：

点圆之间，点心线截距最短（长）。

已知⊙O半径为r，AO=d，P是⊙O上一点，求AP的最大值和最小值。

证明：

由“两点之间，线段最短”得AP≤AO+PO，AO≤AP+PO，得d-r≤AP≤d+r，AP最小时点P在B处，最大时点P在C处。

即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。

（可用“三角形两边之和大于第三边”，其实质也是由“两点之间，线段最短”推得）。

上面几种是解决相关问题的基本图形，所有的几何最值问题都是转化成上述基本图形解决的。

二、考试中出现的问题都是在基本图形的基础上进行变式，如圆与线这些图形不是直接给出，而是以符合一定条件的动点的形式确定的；再如过定点的直线与动点所在路径不相交而需要进行变换的。

类型分三种情况：

（1）直接包含基本图形；

（2）动点路径待确定；（3）动线（定点）位置需变换。

（一）直接包含基本图形。

例1.在⊙O中，圆的半径为6，∠B=30°，AC是⊙O的切线，则CD的最小值是。

简析：

由∠B=30°知弧AD一定，所以D是定点，C是直线AC上的动点，即为求定点D到定线AC的最短路径，求得当CD⊥AC时最短为3。

（二）动点路径待确定。

例2.，如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是。

简析：

A是定点，B是动点，但题中未明确告知B点的运动路径，所以需先确定B点运动路径是什么图形，一般有直线与圆两类。

此题中B的路径是以C为圆心，BC为半径的圆弧，从而转化为定点到定圆的最短路径为AC-BC=1。

例3.在△ABC中，AB=AC=5，cos∠ABC=3/5，将△ABC绕点C顺时针旋转，得到△ABC，点E是BC上的中点，点F为线段AB上的动点，在△ABC绕点C顺时针旋转过程中，点F的对应点是F，求线段EF长度的最大值与最小值的差。

简析：

E是定点，F是动点，要确定F点的运动路径。

先确定线段AB的运动轨迹是圆环，外圆半径为BC，内圆半径为AB边上的高，F是AB上任意一点，因此F的运动轨迹是圆环内的任意一点，由此转化为点E到圆环的最短和最长路径。

E到圆环的最短距离为EF2=CF2-CE=4.8-3=1.8，E到圆环的最长距离为EF1=EC+CF1=3+6=9，其差为7.2。

（三）动线（定点）位置需变换。

线段变换的方法：

（1）等值变换：

翻折、平移；

（2）比例变换：

三角、相似。

【翻折变换类】典型问题：

“将军饮马”。

例4.如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长最小值为。

简析：

动线段（或定点）应居于动点轨迹的两侧，本题的三条动线段PM、MN、PN在OA、OB的内侧。

所以本题的关键是把定线段变换到动点轨迹的两侧，从而把三条动线段PM、MN、PN转化为连接两点之间的路径。

如图，把点P分别沿OA、OB翻折得P1、P2，△PMN的周长转化为P1M+MN+P2N，这三条线段的和正是连接两个定点P1、P2之间的路径，从而转化为求P1、P2两点之间最短路径，得△PMN的周长最小值为线段P1P2＝OP＝6。

例5.如图，在锐角△ABC中，AB=4，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是。

简析：

本题的问题也在于动线段BM、MN居于动点轨迹AD的同侧，同样把点N沿AD翻折至AC上，BM+MN＝BM+MN，转化为求点B到直线AC的最短路径，即BN⊥AC时，最小值为2√2。

【平移变换类】典型问题：

“造桥选址”。

例6.如图，m、n是小河两岸，河宽20米，A、B是河旁两个村庄，要在河上造一座桥，要使A、B之间的路径最短应该如何选址（桥须与河岸垂直）？

简析：

桥长为定值，可以想像把河岸m向下平移与n重合，同时把点A向下平移河宽，此时转化成n上的一点到A、B的路径之和最短，即转化为定点A到定点B的最短路径。

如下图：