有关角分线的典型题型.docx

有关角分线的典型题型.docx

《有关角分线的典型题型.docx》由会员分享，可在线阅读，更多相关《有关角分线的典型题型.docx（17页珍藏版）》请在冰豆网上搜索。

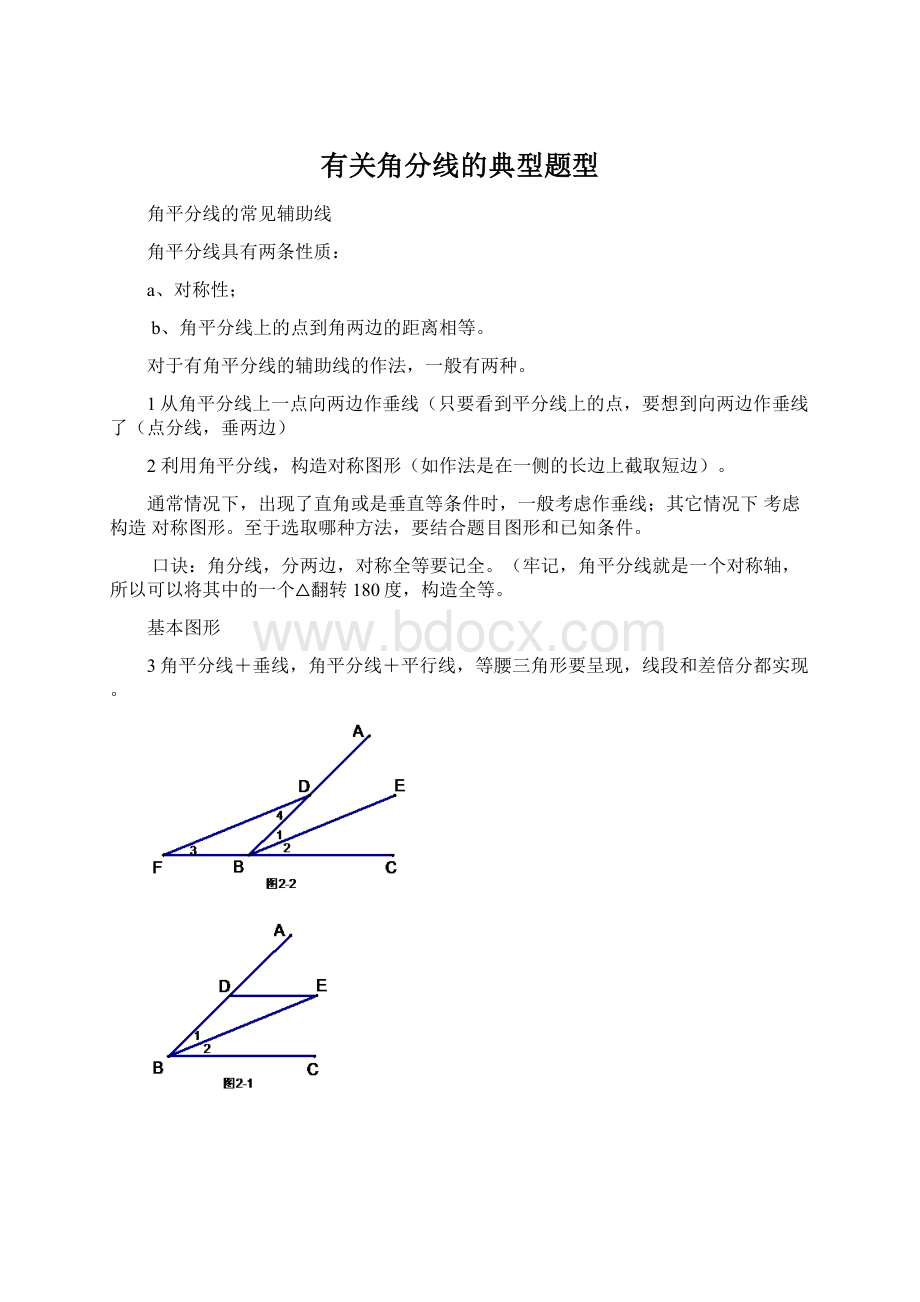
有关角分线的典型题型

角平分线的常见辅助线

角平分线具有两条性质：

a、对称性；

b、角平分线上的点到角两边的距离相等。

对于有角平分线的辅助线的作法，一般有两种。

1从角平分线上一点向两边作垂线（只要看到平分线上的点，要想到向两边作垂线了（点分线，垂两边）

2利用角平分线，构造对称图形（如作法是在一侧的长边上截取短边）。

通常情况下，出现了直角或是垂直等条件时，一般考虑作垂线；其它情况下考虑构造对称图形。

至于选取哪种方法，要结合题目图形和已知条件。

口诀：

角分线，分两边，对称全等要记全。

（牢记，角平分线就是一个对称轴，所以可以将其中的一个△翻转180度，构造全等。

基本图形

3角平分线＋垂线，角平分线＋平行线，等腰三角形要呈现，线段和差倍分都实现。

典例分析

（一）、截取构全等

如图1-1，∠AOC=∠BOC，如取OE=OF，并连接DE、DF，则有△OED≌△OFD，从而为我们证明线段、角相等创造了条件。

例1．如图1-2，AB//CD，BE平分∠ABC，CE平分∠BCD，点E在AD上，求证：

BC=AB+CD。

分析：

此题中就涉及到角平分线，可以利用角平分线来构造全等三角形，即利用解平分BFC图1-2线来构造轴对称图形，同时此题也是证明线段的和差倍分问题，在证明线段的和差倍分问题中常用到的方法是延长法或截取法来证明，延长短的线段或在长的线段长截取一部分使之等于短的线段。

但无论延长还是截取都要证明线段的相等，延长要证明延长后的线段与某条线段相等，截取要证明截取后剩下的线段与某条线段相等，进而达到所证明的目的。

简证：

在此题中可在长线段BC上截取BF=AB，再证明CF=CD，从而达到证明的目的。

这里面用到了角平分线来构造全等三角形。

另外一个全等自已证明。

此题的证明也可以延长BE与CD的延长线交于一点来证明。

自已试一试。

例2．已知：

如图1-3，AB=2AC，∠BAD=∠CAD，DA=DB，求证DC⊥AC

分析：

此题还是利用角平分线来构造全等三角形。

构造的方法还是截取线段相等。

其它问题自已证明。

例3．已知：

如图1-4，在△ABC中，∠C=2∠B,AD平分∠BAC，求证：

AB-AC=CD

分析：

此题的条件中还有角的平分线，在证明中还要用到构造全等三角形，此题还是证明线段的和差倍分问题。

用到的是截取法来证明的，在长的EA线段上截取短的线段，来证明。

试试看可否把短的延长来证明呢？

练习

1．已知在△ABC中，AD平分∠BAC，∠B=2∠C，求证：

AB+BD=AC

2．已知：

在△ABC中，∠CAB=2∠B，AE平分∠CAB交BC于E，AB=2AC，求证：

AE=2CE3．已知：

在△ABC中，AB>AC,AD为∠BAC的平分线，M为AD上任一点。

求证：

BM-CM>AB-AC

4．已知：

D是△ABC的∠BAC的外角的平分线AD上的任一点，连接DB、DC。

求证：

BD+CD>AB+AC。

（二）角分线上点向角两边作垂线构全等

过角平分线上一点向角两边作垂线，利用角平分线上的点到两边距离相等的性质来证明问题。

例1．如图2-1，已知AB>AD,∠BAC=∠FAC,CD=BC。

求证：

∠ADC+∠B=180°

分析：

可由C向∠BAD的两边作垂线。

近而证∠ADC与∠B之和为平角。

例2．如图2-2，在△ABC中，∠A=90°，AB=AC，∠ABD=∠CBD。

求证：

BC=AB+AD

分析：

过D作DE⊥BC于E，则AD=DE=CE，则构造出全等三角形，从而得证。

此题是证明线段的和差倍分问题，从中利用了相当于截取的方法。

例3．已知如图2-3，△ABC的角平分线BM、CN相交于点P。

求证：

∠BAC的平分线也经过点P。

分析：

连接AP，证AP平分∠BAC即可，也就是证P到AB、AC的距离相等。

练习：

如图所示，∠1=∠2，P为BN上的一点，并且PD⊥BC于D，AB＋BC=2BD。

求证：

∠BAP＋∠BCP=180°。

证明：

经过点P作PE⊥AB于点E。

因为PE⊥AB，PD⊥BC，∠1=∠2，所以PE=PD。

在Rt△PBE和Rt△PBC中

，所以Rt△PBE≌Rt△PBC（HL），

所以BE=BD。

因为AB＋BC=2BD，BC=CD＋BD，AB=BE－AE，

所以AE=CD。

因为PE⊥AB，PD⊥BC，所以∠PEB=∠PDB=90°.

在△PAE和Rt△PCD中

，所以△PAE≌Rt△PCD，所以∠PCB=∠EAP。

因为∠BAP＋∠EAP=180°，所以∠BAP＋∠BCP=180°

练习：

1．如图2-4∠AOP=∠BOP=15°PC//OA，PD⊥OA，如果PC=4，则PD=（）

2．已知在△ABC中，∠C=90，AD平分∠CAB，CD=1.5,DB=2.5.求AC.

3．已知：

如图2-5,∠BAC=∠CAD,AB>AD，CE⊥AB，AE=

.求证：

∠D+∠B=180。

4．已知：

如图2-6,在正方形ABCD中，E为CD的中点，F为BC上的点，∠FAE=∠DAE。

求证：

AF=AD+CF。

5．图2-5已知：

如图2-7，在Rt△ABC中，∠ACB=90,CD⊥AB，垂足为D，AE平分∠CAB交CD于F，过F作FH//AB交BC于H。

求证CF=BH。

（三）：

作角平分线的垂线构造等腰三角形

从角的一边上的一点作角平分线的垂线，使之与角的两边相交，则截得一个等腰三角形，垂足为底边上的中点，该角平分线又成为底边上的中线和高，以利用中位线的性质与等腰三角形的三线合一的性质。

（如果题目中有垂直于角平分线的线段，则延长该线段与角的另一边相交）

例1．已知：

如图3-1，∠BAD=∠DAC，AB>AC,CD⊥AD于D，H是BC中点。

求证：

DH=

分析：

延长CD交AB于点E，则可得全等三角形。

问题可证。

有和角平分线垂直的线段时，把它延长可得到中点或相等的线段，从而与三角形中位线或三角形全等建立起联系．

例2．已知：

如图3-2，AB=AC，∠BAC=90，BD为∠ABC的平分线，CE⊥BE.求证：

BD=2CE。

分析：

给出了角平分线给出了边上的一点作角平分线的垂线，可延长此垂线与另外一边相交，近而构造出等腰三角形。

例3．已知：

如图3-3在△ABC中，AD、AE分别∠BAC的内、外角平分线，过顶点B作BN垂直AD,交AD的延长线于F，连结FC并A延长交AE于M。

求证：

AM=ME。

分析：

由AD、AE是∠BAC内外角平分线，可得EA⊥AF，从而有BF//AE，所以想到利用比例线段证相等。

例3．已知：

如图3-4，在△ABC中，AD平分∠BAC，AD=AB，CM⊥AD交AD延长线于M。

求证：

AM=

分析：

题设中给出了角平分线AD，自然想到以AD为轴作对称变换，作△ABD关于AD的对称△AED，然后只需证DM=

。

另外由求证的结果AM=

，即2AM=AB+AC，也可尝试作△ACM关于CM的对称△FCM，然后只需证DF=CF即可。

练习2、如图，已知：

ΔABC中AD垂直于∠C的平分线于D，DE∥BC交AB于E.

求证：

EA=EB。

分析：

由AD垂直于∠C的平分线于D，可以想到等腰三角形

中的三线合一，于是延长AD交BC与点F，得D是AF的

中点，又因为DE∥BC，由三角形中位线定理得EA=EB。

证明：

延长AD交BC与点F，∵CD平分∠ACF，∴∠1=∠2，又AD⊥CD，∴ΔADC≌ΔFDC，∴AD=FD，又∵DE∥BC，∴EA=EB。

练习：

1．已知：

在△ABC中，AB=5，AC=3，D是BC中点，AE是∠BAC的平分线，且CE⊥AE于E，连接DE，求DE。

2．已知BE、BF分别是△ABC的∠ABC的内角与外角的平分线，AF⊥BF于F，AE⊥BE于E，连接EF分别交AB、AC于M、N，求证MN=

已知：

如图，

中，D、E在BC上，且DE=EC，

过D作DF∥AB,交AE于点F，DF=AC.求证：

AE平分

.

（四）以角分线上一点做角的另一边的平行线

有角平分线时，常过角平分线上的一点作角的一边的平行线，从而构造等腰三角形。

或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交，从而也构造等腰三角形。

如图4-1图4-2所示。

例4如图，AB>AC,∠1=∠2，求证：

AB－AC>BD－CD。

例5如图，BC>BA，BD平分∠ABC，且AD=CD，求证：

∠A+∠C=180。

例6如图，AB‖CD，AE、DE分别平分∠BAD各∠ADE，求证：

AD=AB+CD。

练习：

1.已知，如图，∠C=2∠A，AC=2BC。

求证：

△ABC是直角三角形。

2．已知：

如图，AB=2AC，∠1=∠2，DA=DB，求证：

DC⊥AC

3．已知CE、AD是△ABC的角平分线，∠B=60°，求证：

AC=AE+CD

4．已知：

如图在△ABC中，∠A=90°，AB=AC，BD是∠ABC的平分线，求证：

BC=AB+AD

（五）角平分线且垂直一线段，应想到等腰三角形的中线例

6．如图7，ΔABC是等腰直角三角形，∠BAC=90°，BD平分∠ABC交AC于点D，CE垂直于BD，交BD的延长线于点E。

求证：

BD=2CE。

证明：

延长BA，CE交于点F，在ΔBEF和ΔBEC中，∵∠1=∠2，BE=BE，∠BEF=∠BEC=90°，∴ΔBEF≌ΔBEC，∴EF=EC，从而CF=2CE。

又∠1+∠F=∠3+∠F=90°，故∠1=∠3。

7在ΔABD和ΔACF中，∵∠1=∠3，AB=AC，∠BAD=∠CAF=90°，∴ΔABD≌ΔACF，∴BD=CF，∴BD=2CE。

注：

此例中BE是等腰ΔBCF的底边CF的中线。

（六）借助角平分线造全等

1：

如图，已知在△ABC中，∠B=60°，△ABC的角平分线AD,CE相交于点O，求证：

OE=OD

2：

（06郑州市中考题）如图，△ABC中，ABDCD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F.

（1）说明BE=CF的理由；

（2）如果AB=a，AC=b，求AE、BEA的长.

（06北京中考）如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形。

请你参考这个作全等三角形的方法，解答下列问题：

（1）如图②，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，、相交于点F。

ADCE请你判断并写出FE与FD之间的数量关系；

（2）如图③，在△ABC中，如果∠ACB不是直角，而

（1）中的其它条件不变，B请问，你在

（1）中所得结论是否仍然成立？

若成立，请证明；若不成立，请说明

练习：

如图，

中，AB=AC，BD、AM分别是

的平分线，

．

求证：

．

3．已知：

如图，

，OE平分

，直线PRQ分别交OX、OE、OY于点P、R、Q．求证：

．

（七）与角平分线相关的作图题举例

1、如图1所示，校园内有两条公路OA、OB，在交叉路口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置距离两块宣传牌一样远，并且到两条公路的距离也一样远。

请你画出灯柱的位置P。

分析：

线与线相交成点，所以要想作出满足条件的点，就相当于作出相应的两条直线，它们的交点就是所求作的点。

解：

如图2所示，作∠AOB的平分线和线段CD的垂直平分线，相交于点P。

点P就是所求作的点。

2、如图3所示，要在两条公路的中间修建一座加油站，位置选在到两条公路的距离相等，并且到两条公路交叉点A处的距离为2cm（指的是图上距离）。

请你设计出加油站的位置，并说明你的理由。

分析：

在实际生活中，会经常用到角平分线的性质定理和逆定理，解决此类问题的关键是从实际问题中构造出数学模型，然后利用数学知识解决问题。

解：

如图4所示，作∠BAC的角平分线AD，在AD上截取AP，使AP=2cm。

点P就是所求作的点。

3、如图5所示，有一块三角形的空地，其三边长分别为20m、30m、40m，现在要把它分成面积比为2：

3：

4的三部分，分别种植不同的花。

请你设计出一个方案，并说明你的理由。

分析：

要想以长为20m、30m、40m的边构造三角形，并且使它们的面积之比为2：

3：

4。

如果以长为20m、30m、40m的边为三角形的底，那么它们相应的高应该相等。

要想使它们的高相等，通过作两个内角的角平分线就可以，角平分线的交点就是三角形的第三个顶点。

解：

方案：

如图6所示，分别作∠C和∠B的角平分线，它们相交于点P，连结PA。

则△PAB、△PAC、△PBC的面积之比就是2：

3：

4。

理由：

经过点P作PE⊥AB于点E，PF⊥AC于点F，PH⊥BC于点H。

因为点P是∠C和∠B的角平分线上的点，所以PE=PF=PH。

所以

，

，

，所以

。

与三角形的角平分线有关的结论的探究

三角形的内角和等于1800，三角形的外角等于和它不相邻的两个内角的和。

应用以上定理和推论可以探究与三角形的角平分线有关的结论。

从结论的探究过程中，希望同学们能从中得到有益的启示：

在平时的数学学习中，要学会运用所学知识去探索新的结论，学会探究，从而不断地提高自己的数学发现与创新的能力，提高数学学习水平。

探究一：

在

中，∠A，∠B的平分线交于点P，试探究

∠BPC与∠A的关系？

探究：

因为∠BPC在ΔBPC中，由三角形的内角和定理，有：

而由BP，CP分别是∠ABC和∠ACB的角平分线

知：

∠PBC=

，∠PCB=

所以

而在在

中，

所以

故有结论一：

在

中，∠A，∠B的平分线交于点P，则有

。

探究二：

在

中，BP是∠ABC的平分线，CP是ΔABC的外角∠ACE的平分线，

试探究：

∠BPC与∠A的关系？

探究：

由CP是ΔABC的外角∠ACE的平分线，

所以有：

∠BPC=∠PCE－∠BPC

又BP是∠ABC的平分线，CP是∠ACE的平线

所以：

∠PBC=

，∠PCE=

所以∠BPC=

－

故有结论二：

在

中，BP是∠ABC的平分线，CP是ΔABC的外角∠ACE的平分线，

则有：

。

探究三：

在

中，BP，CP分别是ΔABC的两个外角的平分线，

试探究：

∠BPC与∠A的关系？

探究：

因为∠BPC在ΔBPC中，由三角形的内角和定理，有：

由BP，CP分别是ΔABC的两个外角的平分线，有：

∠PBC=

，∠PCB=

而∠ABC+∠CBE=1800，∠ACB+∠BCF=1800，

所以∠ABC+∠CBE+∠ACB+∠BCF=3600

所以∠EBC+∠FCB=3600－（∠ACB+∠ABC）

所以

故有结论三：

在

中，BP，CP分别是ΔABC的两个外角的平分线，

则有

。