极限导数积分计算.docx
《极限导数积分计算.docx》由会员分享,可在线阅读,更多相关《极限导数积分计算.docx(39页珍藏版)》请在冰豆网上搜索。
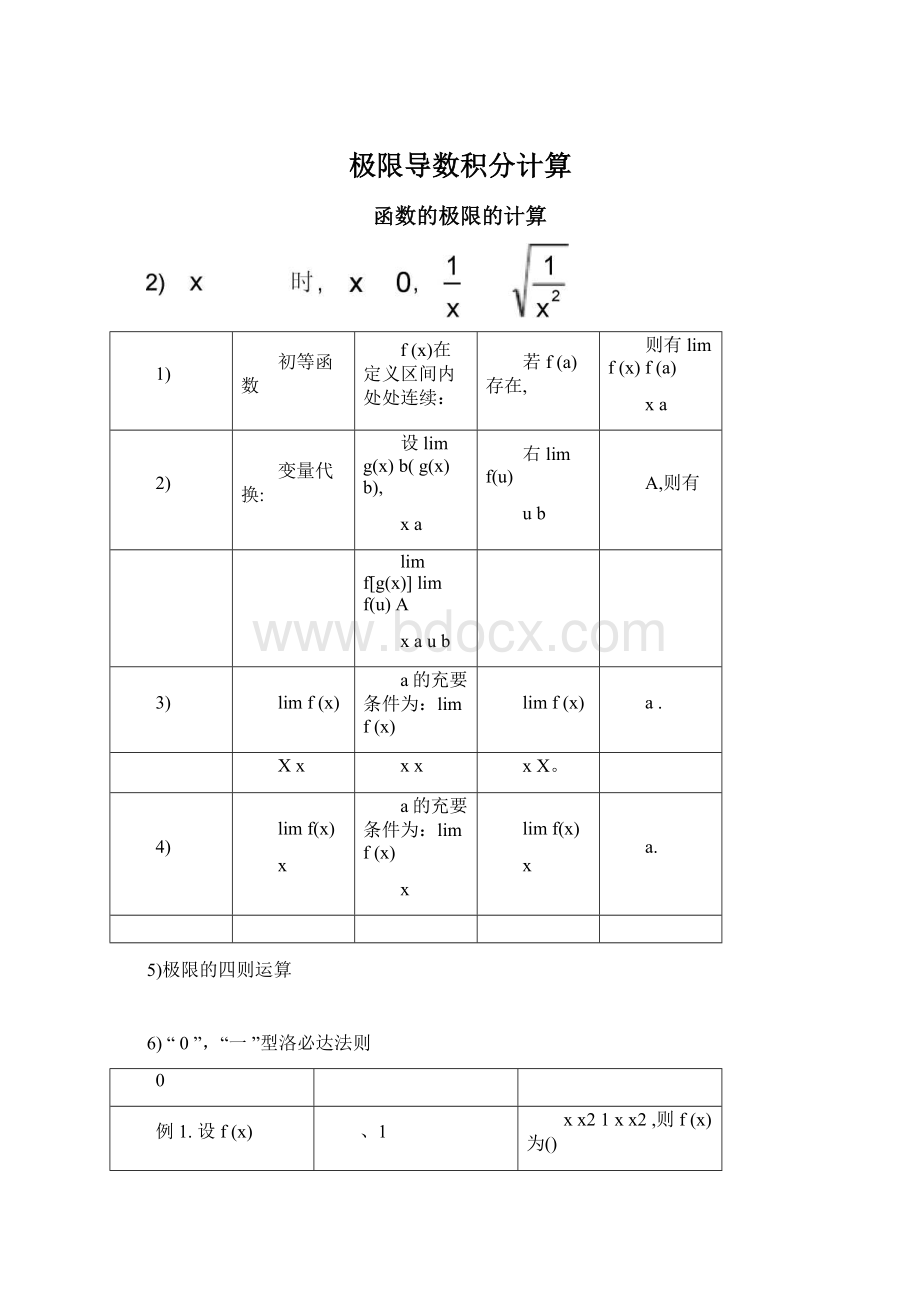
极限导数积分计算
函数的极限的计算
1)
初等函数
f(x)在定义区间内处处连续:
若f(a)存在,
则有limf(x)f(a)
xa
2)
变量代换:
设limg(x)b(g(x)b),
xa
右limf(u)
ub
A,则有
limf[g(x)]limf(u)A
xaub
3)
limf(x)
a的充要条件为:
limf(x)
limf(x)
a.
Xx
xx
xX。
4)
limf(x)
x
a的充要条件为:
limf(x)
x
limf(x)
x
a.
5)极限的四则运算
6)“0”,“一”型洛必达法则
0
例1.设f(x)
、1
xx21xx2,则f(x)为()
A.有界函数;
B.
偶函数;
C.limf(x)
x
1;D.
limf(x)1.
x
解题提示:
1)
f(x)为
奇函数.
3)|f(x)||f(|x|)|
2|x|
2.
1|x|
x2J|x|x2
例2.下列各式中不正确的是(
).
1
1
1
A.limex;B.
limex
;C.limex
0;D
x0
1
x0
x0
2e,
sinx
例3.求lim(4
.
x0_
|x|
1ex
解题提示:
计算左右极限
1
limex1.
x
洛必达法则是计算极限的有效方法例4.计算下列极限:
tanx1
1)lim;2)
x-sin4x
4
1
4)lim(—
x0x
十);
解题提示:
5)令x
ln(1lim-x
5)
t
sin3x
例5.右lim[一3
x0x
sin3x
解题提示:
3-
x
0Inx
lim[x
x
或ln(1
f(x)]
2xf(x)
2
丄)
乂;3)
x2
丄)
x
ln(1
0,计算
sin3x3x
!
呼21nX;
丄)].
x
11
2x2
lim—W
x0
2
x
3f(x)
极限计算中无穷小的处理:
“0根
在乘除运算中,极限值不为0的因子先算出,“0因子”作等价无穷小代换式”有理化•
3
limx2(x22x1
x
x)
lim12U21U1
u0
f(x)sinx1
2,求limf(x).
x0
例9.已知lim3x
x0e3x1
解题提示:
利用等价无穷小代换计算左式
极限计算中无穷大的处理:
“根式”有理化.
“三角无穷大”的导数仍然为无穷大,“三角无穷大”要先变.
求x时的极限,分子,分母同时除以分子,分母中的最高次幕(“抓大头”方法中的“大头”).所谓“抓大头”就是抓住关于x的最高次的项,而把其余的项略掉.如
nn
anX6Xa。
广anX
lim匚--lim匚.
xbmX0Xb°xbmX
例10.计算下列极限:
1)
tan3x
lim;2)
xtanx
2
lim
X
x(x25
.X21)
4x2x
1X1
3)
lim(..x210xx);4)
lim
:
2
X
X
X
sinx
在计算极限时,洛必达法则不要“滥用”
例11.
计算lim
x
解题提示:
用洛必达法则,观察会出现怎样的情形
xsinx例12.lim().
xxsinx
A.1B.不存在C.0D.1
解题提示:
1)分析以下错误运算:
xsinxlim
xxsinx
2)分析以下错误运算:
xsinxlim
xxsinx
..1
cosx
lim
-
1
cosx
1
sin-
lim
-
-
1
sin-
-
0.
sinxlim
xsinx
1.
例13.求lim
x
解题提示:
1)
xx
eex
xx
eex
先多次用洛必达法则
观察会出现怎样的情形
n
2)lim电xe
Inx为x的0次幕.
3)分子,分母同时除以分子,分母中的最高次幕
1
e
—.
x
试用洛必达法则看看.
lnx
lim—n-0(n为正数),当x
x
时,可认为ex为x的无穷大次
即用“抓大头”方法.
例14.求lim
x
解题提示:
1)
1
2)令t
limuv(
其中的“
“1
。
0。
”
型,也可用配
型)极限计算法:
ln(lim
e法:
uv)limvlnu.
0,limv(x)
设limu(x)
例15.计算下列极限:
1
lim(1u)vlim[(1u)u]uv
limuv
e
1)lim(sin仝cos-)n;2)
nnn
lim(1
x
1
x)l3)
xm(2arctanx)lnx
利用导数定义式计算极限
例16.设f(x)在xa处可导,
f(x)
0,
1
求lim[f(a)/f(a)]n.nn
f(a
解题提示:
利用配e法,计算lim
n
n[
1
-)
n
f(a)
1].
例17.设f(X)在点xo处有二阶导数,求极限
f(Xoh)2f(Xo)f(Xoh)lim2
h0h2
解题提示:
先用一次洛必达法则•
注意:
因二阶导数f(x)在点Xo处连续性不知,不可再次用洛必达法则
o
X
f
mo
Hh
h)2f(Xo)f(Xoh)
X
/V-T
mo
Hh
x0
lim1陛
ho2h
h)f(Xo)f(Xo
h)f(Xo)]f(Xo).
利用中值定理计算极限例18.计算下列极限:
2
1)limx[Inarctan(x1)Inarctanx];
X
x2
c\x
2)limarctanxdx.
xxx1
解题提示:
1)对函数f(t)lnarctant在[x,x
1arctan
Inarctan(x1)Inarctanx
1]上用拉格朗日中值定理
1
1
X1).
2)利用积分中值定理,
x2x
arctanxdx
xx1
arctan
2).
利用麦克劳林公式计算极限例19.计算下列极限:
~2
-;2)
1)limcoSX4e
xosinx
解:
1)sin
cosx
lim(1
xo
2
1•
2
1
~2
X
4
X
24
ln2
2
o(x4),
cosx
2
X
2
~2
1疋
24
4
X
12
2
O(x4),
O(
X4),
1
12.
x.
ln
(1)
2
e
.4—sinx
xln(1x
W)2
22
13
一X12
丄
2
cosxlim
x0
2)ln-
2
[f
o(x3)]
o(x3)]
Xmo(1
O(x3),
12x
尹厂)Xmo[1
1
12
o(x3)]
3]
11
12
二.导数与微分的计算
1)四则运算求导公式.
2)复合函数求导公式:
[f(g(x))]f(g(x))g(x).
3)微分计算公式:
df(x)f(x)dx.
注意:
微分等式中变量x可用任意可导函数g(x)作代换.
.2
参数方程求导公式:
dydydxdy
4)
dx
5)
6)
7)
2g
dxdtdtdx2dtdx.dt
隐函数求导法:
方程两边同时对x求导,注意f(y)中y为中间变量.幕指函数求导公式:
{[f(x)]g(x)}[f(x)]g(x)[g(x)lnf(x)].
取对数求导法:
设y[f1(X)]1(x)[fn(x)]n(x),则有
lny1(x)lnf1(x)n(x)lnfn(x)
pl
f(x)为连续函数,则有一[f(x)dx]f(x).
dx
f(x)为连续函数,u(x),v(x)可导,则有变限积分函数求导公式
1(x)
n(x)
ddx
u(x)
f(t)dt
v(x)
例1.
设f(x)
sinx则-
设
8)
设
9)
f[u(x)]u(x)f[v(x)]v(x)
例2.
例3.
解题提示:
yf(u)可导,
yInx,当x
自变量的微分等于自变量的增量
df(、x)
dx
yf[ef(x)],则dy
2,x0.01时,dy
,即dxx.
例4.
f(x)dxIn1
dx11
例5.
f(x)为连续函数,且F(X)
lnx
if(t)dt,则F(x)
x
例6.
解题提示:
0
dx22
求xf(t)dt,其中f(t)为已知的连续函数.
dx0
x2
x2f(t)dtx2
x2
0f(t)dt.
xf(x
解题提示:
令u
xt,
1
0
f(x
t)dt
x
f(u)
du.
例8.设
f(x)
x(x
1)(
x2)
(xn),则
f(0)
解题提示:
f(x)
(x
1)
(x
n)x[(x1)
(x
n)]
例9.若
f(x)
f(:
x),
在(0,
)内f(x)
0,f
(x)
1.
(A)f(x)
0,f
(x)
0;
(B)
f(x)0,f
(x)
0;
(C)f(x)
0,f
(x)
0;
(D)
f(x)0,f
(x)
0.
其中f(t)为已知的连续函数.
t)dt.
0
0,则f(x)在(
解题提示:
f(x)为偶函数.试证明:
1)可导偶函数的导数为奇函数;
2)可导奇函数的导数为偶函数.
()
x2
xx2
x2
例7.求—dx
0)内
例10.设函数yy(x)由方程xef(y)ey确定,其中f具有二阶导数,且f1,求
dx2.
高阶导数与泰勒公式
n
1)莱布尼兹公式:
(uv)(n)Cnu(nk)v(k).
k0
3)函数f(x)在点xa处带皮亚诺型余项的n阶泰勒展开式:
f(n)(a)
f(x)f(a)f(a)(xa)(xa)no[(xa)n]
n!
例13.求下列函数的n阶导数:
1)yln(x1);
2)ycoskx;
x
3)yxe;
x
4)yecosx.
5)
ysinxsin3x.
y(n)(.2)nexcos(x—).
4
例14.求函数f(x)ln(1x)在点x0处带拉格朗日型余项的n阶泰勒展开式
例16.设f(x)
解题提示:
f(x)
x10
TV则f
(x9
(10)/、
(x)
x1),
2x
例17.求函数f(x)xe在x0处的n阶导数
宀⑺
ax
f(n)(0)(n
n!
n1
(ax)
3).
例仆.求函数f(x)x21n(1x)在点x0处带皮亚诺型余项的5阶泰勒展开式
n
解题提示:
1)利用莱布尼兹公式(uv)(n)cfu'nk)v(k).
2)利用ex1x
n!
o(xn)及麦克劳林公式
解:
ex
n!
0(xn)
f(x)
(n2)!
0小
(n)(0)
n!
(n)(0)n(n1).
例18.设
f(x)x,
x
0
5
求f
⑷(0)
1,
x
0
3
5
(
n1
2n1
解题提示:
xsinxx
x
1)
x
3!
5!
(2n
1)!
例19.设
1.
\/ameinx
y求
(n)
(0)
'1X2、
求
y
(0丿.
解题提示:
建立递推公式(1
x2
)y(n
1)
(2n
1)xy
(n2)!
sinx
(n)
o(x2n1).
n2y(n1)
0.
三.不定积分的计算:
1.常用公式
tanxdx
In|cosx|C;
cotxdx
In
|sinx|
C;
In|cscx
cotx|C;
dx
1+x
arctanaa
C;
dx
1l
22xa
22xa
2a
dx
.x
C;
dx
In
-arcsin
C;
secxdx
In|secxtanx|
cscxdx
a
*
x
|xx2a2|C.
、a2x2
22xa
2.分项法:
通过代数或三角恒等变形把所给不定积分化为基本积分公式中的积分或常见的积分类型.
alc;
a
例1.计算下列不定积分
4
x,
1)2dx;2)
1x
1
22dx;
sinxcosx
3)
xsinx
1cos2x
dx.
3.第一换元法(凑微分法):
设F为f的原函数,u
(x)可导,贝贿
f[(x)](x)dx
f[(x)]d(x)[凑微分:
(x)dxd(x)]
F[(x)]C.
[换元:
f(x)dxF(x)
C中x换为(x)]
如何确定中间变量u(x)?
A)从被积函数明显的复合部分f(u)去确定u.
B)通过凑微分确定u.
C)从被积函数中复杂的部分去确定u.
例2.计算下列不定积分:
丄2-x.lntanx1
1)tanx1dx;2)dx;3)
Jx21sinxcosx
4)
dx;
dx
7);
vx(1x)
解题提示:
8)(excosx)
dxx
5)x;6)4dx;
2e11x
cosxsinx
8)xdx.
cosx(1ecosx)
ex(cosxsinx).
4.第二换元法(积分变量代换法):
设x(t)单调可导,则有
f(x)dxf[(t)](t)dt.
例4.
解题提示:
(x
2
x
dx
1)2、x22x
2x(x1)2
1,作代换
sect.
积分变量代换法常见的有:
5.分部积分法:
udvuvvdu.
常见类型有:
1)P(x)sin(axb)dx,P(x)cos(axb)dx,P(x)eaxdx.取uP(x).
2)xnlnP(x)dx,xnarctanxdx等.取dvxndx.
3)secxdx,eaxsinbxdx,eaxcosbxdx.用分部积分法回归”
例5.
计算下列不定积分
1)
(x2x)sin2xdx;
2)
(x2x1)exdx;
3)
Inx,
2dx;(1x);
arctanx
ax
lncosx
4)
2dx;
5)
ecosbxdx;
6)
2dx;
x
cosx
xsin2x,
arctanx,
7)
dx;
8)
22dx;
9)
sinlnxdx.
1cos2x
x(1x)
例6.求a2x2dx.
解题提示:
1)令xasint.
2)分部积分回归法.
2
x
例7.求「dx.
(1x)
解题提示:
1)分部积分法:
-
(1
2
x.
2、2dx
x)
2)令xtant.
x
xe.
dx.
-..ex1
令tex1.
tan2xsecxdx.
例8.求
解题提示:
例9.求
解题提示:
1)分部积分回归法.
.2sinx
丄2,sinx1
2)tanxsecxdx3dx
cosx
sinxd
1
2~
cosx
注:
凑微分是计算积分的首要过程是积出积分的重要一环主要手段,灵活多变,分题,计算当中会出现
1
;分部积分法是初学时不易掌握恰好”之处.
是求导的逆运算,第一换元法是复合求导的逆运算
乘积”求导的逆运算,是计算积分的一种过度性的
.切记:
初等函数并不是都能积得出”,不常见的积
例10.求
解题提示:
2)分项
(X
Inx,rdx.
(xInx)2
八1Inx
1)—
x
1Inx
Inx)2
宀).
x
1x(Inxx)
例11.
1sinx
例12.
(X
Inx)2
xInx
x
2(xInx).
(xInx)
exdx.
1cosx
沁exdx
1cosx
1sinx
exdx
2cos2-
xx
edtan—
2
2x+xe求2
(x2)2
2x
xe
(x2)2
2x
xe
x2
吨dex
2
xx
etan-
2
dx.
dx
x
(2xe
x2ex)dx
xexdx
x2ex
xx
xeeC
(x2)ex
2C.
6.特殊积分举例
例13.求
解题提示:
例14.求
x3
rdx
x6x5
x32
x26x5x5
4x1」
rdx.
x24x8
解题提示:
4x1
x24x8
2(2x
4)
例15.求
x(x4
1
1)
x(xn
a)
dx
x4
1,
2
)x
1
x
1
1
1-
2
x
2
1
x
2
dx
解题提示:
例16.求
1
解题提示:
xdx
x21
2)4
x
例17.
1sinx
解题提示:
1)
例18.求
例19.求
解题提示:
例20.求
4x
9
2
(x2)4
A1
ax
2
x
-4
x
n
x
n
x
1-).
a
-dx.
1
1
1~~2
x_
1
7
(x1)
x_
〒2
x
(x
令utan:
2
-^dx,
1cosx
sinx
2)
(x
(x
1sinx戲』dx等.
sinx
1sinx
—.化分母为单项
x
cos2
COSX
用此法可计算
asinx
acosx
bcosx
bsinx
asinx
bcosx
asinx
bcosx
asinx
i
bcosx
解题提示:
dx
dx
sin3xcos2xdx.
dx.asinxbcosx
In
m2n1m
sinxcosxsinx
3
cosx,
2dx.sinx
|asinxbcosx|C,
(1sin2x)n(sinx).
解题提示:
cosmxsin2n
例21.求cos4xdx.
cos
mx(1cos2
x)n(cosx)•
解题提示:
1)降幕法
2)分部积分回归法
cosnxdx
1
4(1
建立递推公式:
n1
cos
4
cosx
xdsinx
cos2x)2
n
sinxcos
(n
1)
.2
sinx
n
cos
2xdx
n
sinxcos
(n
1)
n2cos
xdx
(n
1)
cosnxdx,
cosnxdx
1
—sinxcosn
cosx,dx.
cos
2xdx.
1
例22.求—2
3sinx
1
解题提示:
——
3sinx
3cos2x4sin2x
1—(tanx).
x
4tan
四.定积分与广义积分的计算
1.
设
2.
牛顿一莱布尼兹公式
f(x)在[a,b]上连续,且F(x)
b
af(x)dx
定积分的分部积分公式
f(x),
则有
F(b)
F(a).
设u(x),v(x)在[a,b]上连续,则有
b
u(x)dv(x)
a
[u(x)v(x)】a
b
v(x)du(x).
a
3.定积分的换元法
设f(x)在[a,b]上连续,
x(t)在[a,b]上变化,且
x(t)在[
(
()a,
b
af(x)dx
]上单值连续可导,当t在[
)b,则有
f[(t)]
(t)dt.
]上变化时,
例23.计算下列定积分:
1)4tan2xdx;
/0
2)
dx
xJln2x
12
3)0xarctanxdx;
4)
0「cosxdx.
2i
例24.计算X4i4x2dx.
0
解题提示:
1)令x
2sint.
2)记In02
n
sin
xdx02cosnxdX,则有In
3
口I
丨n2・
n
例25.计算ox(1x4)2dx.
解题提示:
令
x2sint
例26.计算
04'nd
tanx)dx.
解题提示:
令
例27.已知f(x)
sin(x
1)2,且f(0)
0,
1
0f(x)dx.
1
解:
°f(x)dx[xf(x)]
2
xsin(x1)dx
1
xf(x)dx
0
1
°sin(x
1)2dx
f(0):
xsin(x1)2dx
1
0°
21211
x)sin(x1)2dxcos(x1)|0(1
22
cosl)
f(x)dx
a
0[f(x)f(x)]dx
1)当
§f(x)是奇函数