数学建模题目及其答案疾病的诊断.docx
《数学建模题目及其答案疾病的诊断.docx》由会员分享,可在线阅读,更多相关《数学建模题目及其答案疾病的诊断.docx(28页珍藏版)》请在冰豆网上搜索。
数学建模题目及其答案疾病的诊断
数学建模疾病的诊断
现要你给出疾病诊断的一种方法。
胃癌患者容易被误诊为萎缩性胃炎患者或非胃病者。
从胃癌患者中抽取5人(编号为1-5),从萎缩性胃炎患者中抽取5人(编号为6-10),以及非胃病者
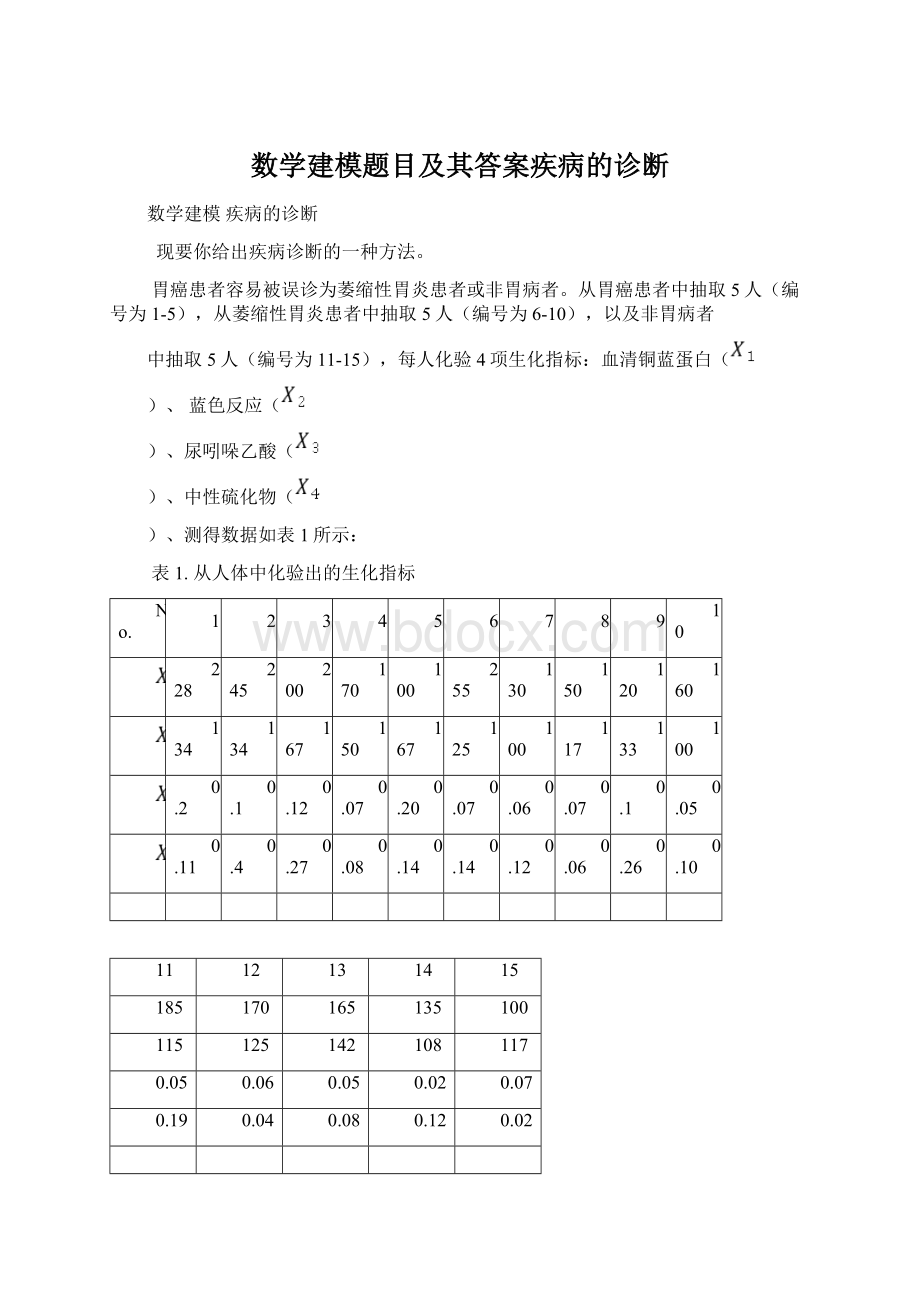
中抽取5人(编号为11-15),每人化验4项生化指标:
血清铜蓝蛋白(
)、蓝色反应(
)、尿吲哚乙酸(
)、中性硫化物(
)、测得数据如表1所示:
表1.从人体中化验出的生化指标
No.
1
2
3
4
5
6
7
8
9
10
228
245
200
170
100
255
130
150
120
160
134
134
167
150
167
125
100
117
133
100
0.2
0.1
0.12
0.07
0.20
0.07
0.06
0.07
0.1
0.05
0.11
0.4
0.27
0.08
0.14
0.14
0.12
0.06
0.26
0.10
11
12
13
14
15
185
170
165
135
100
115
125
142
108
117
0.05
0.06
0.05
0.02
0.07
0.19
0.04
0.08
0.12
0.02
根据数据,试给出鉴别胃病的方法。
论文题目:
胃病的诊断
摘要
在临床医学中,诊断试验是一种诊断疾病的重要方法。
好的诊断试验方法将对临床诊断的正确性和疾病的治疗效果起重要影响。
因此,对于不同疾病不断发现新的诊断试验方法是医学进步的重要标志。
传统的诊断试验方法有生化检测、DNA检测和影像检测等方法。
而本文则通过利用多元统计分析中的判别分析及SPSS软件的辅助较好地解决了临床医学中胃病鉴别的问题。
在临床医学上,既提高了临床诊断的正确性,又对疾病的治疗效果起了重要效果,同时也减轻了病人的负担。
判别分析是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
其基本原理是按照一定的判别准则,建立一个或多个判别函数,用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标。
首先,由判别分析定义可知,只有当多个总体的特征具有显著的差异时,进行判别分析才有意义,且总体间差异越大,才会使误判率越小。
因此在进行判别分析时,有必要对总体多元变量的均值进行是否不等的显著性检验。
其次,利用判别分析中的费歇判别和贝叶斯判别进行判别函数的建立。
最后,利用所建立的判别函数进行回判并测得其误判率,以及对其修正。
本文利用SPSS软件实现了对总体间给类变量的均值是否不等的显著性检验并根据样本建立了相应的费歇判别函数和贝叶斯判别函数,最后进行了回判并测得了误判率,从而获得了在临床诊断中模型,给临床上的诊断试验提供了新方法和新建议。
关键词:
判别分析;判别函数;Fisher判别;Bayes判别
一问题的提出
在传统的胃病诊断中,胃癌患者容易被误诊为萎缩性胃炎患者或非胃病患者,为了提高医学上诊断的准确性,也为了减少因误诊而造成的病人死亡率,必须要找出一种最准确最有效的诊断方法。
为诊断疾病,必须从人体中提取4项生化指标进行化验,即血清铜蓝蛋白、蓝色反应、尿吲哚乙酸、中性硫化物。
但是,从人体中化验出的生化指标,必须要确定一个精准的指标来判断疾病所属的类型。
设想,使用判别分析法,利用SPSS软件对各个变量进行系统的分析,使该问题得到有效地解决。
二、问题的分析
由题意可知,目的就是为了建立一种模型,解决医学上的这种误诊问题。
在该问题中,必须确定血清铜蓝蛋白、蓝色反应、尿吲哚乙酸、中性硫化物与胃癌、萎缩性胃炎的关系。
衡量该四项指标的数学要点必然是相应的标准差、方差、均值等,同时,会建立一个或几个函数分析其间关系的正相关或负相关,即其具有一定的相关性,然后利用所给数据求解出一定的数学模型表达式,便可求解出胃病的鉴别方法。
三、符号的说明
X1:
血清铜蛋白
X2:
蓝色反应
X3:
尿吲哚乙酸
X4:
中型硫化物
N:
被调查的样本数
Wilks的lambda:
组内平方和与总平方和之比(当所有观测的组均值相等时,Wilks的lambda值为1;当组内变异与总变异相比小时,Wilks的lambda值接近于0。
因此,Wilks的lambda值大,表示各个组的均值基本相等;Wilks的lambda小表示组间有差异。
在判别分析中,只有组均值不等时,判别分析才有意义)
F:
F值,F分布中的统计检定值
df:
自由度
sig.:
统计显著性,即出现目前样本的机率
P:
p值
四、问题的假设
1.该四项生化指标是分别可以测得的。
2.每个生化指标都不是其他三个指标的线性组合,即两两之间无相关性。
3.被抽取的三类人员中彼此没有任何血缘关系。
4.除了本题研究的疾病外,被调查的人员无任何疾病。
五、模型的建立
根据以上的分析,回忆所学的知识,发现该问题符合判别分析法的要求,因此可以用判别分析法来求解,其中,判别分析法可以分为:
距离判别法、Fisher判别法、Bayes判别法等。
SPSS软件是统计分析软件之一,它可以进行各种统计分析工作。
另外,它所具有的强大的图形输出功能,使运行该软件不仅可以得到各种数字分析结果,还可以得到各种直观、清晰、漂亮的统计图形。
从而利用软件SPSS,将所有的数据输入进去,便可以得到协方差矩阵、自由度、p值、均值、标准差等与该问题相关的有利于分析问题的数据及图形。
现在主要利用Fisher判别法、Bayes判别法来处理该问题。
Fisher判别法的基本思想:
从
个总体中抽取具有
个指标的样品观测数据,借助方差分析的构造一个线性判别函数:
,其中系数
确定的原则是使得总体之间区别最大,而使每个总体内部的离差最小。
有了线性判别函数U后,对于一个新的样品,将它的
个指标值代入以上线性判别函数式中求出
值,然后根据判别一定的规则,就可以判别新的样品属于哪个总体。
Bayes判别法的基本思想:
设有
个总体
,其各自的分布密度函数
互不相同的,假设
个总体各自出现的概率分别为
(先验概率),
,
。
假设已知若将本来属于
总体的样品错判到总体
时造成的损失为
,
。
在这样的情形下,对于新的样品
判断其来自哪个总体。
通过这两种方式利用软件SPSS来求解,得出的数据在分析比较后,就可以得出结果。
六、模型的求解
1.spss操作步骤如下
(1)建立数据文件
在数据窗口中输入上入待分析的数据。
(2)按顺序单击分析→分类→判别菜单项,如图-1所示,系统弹出判别分析的对话框,如图-2所示
图-1先选择菜单进入判别分析对话框
注:
X1:
血清铜蛋白
X2:
蓝色反应
X3:
尿吲哚乙酸
X4:
中型硫化物
(3)选择参与判别分析的变量及其他相关设置
1)分组变量框:
从左侧选入分类变量“类型”于分组变量框中。
2)定义范围按钮:
定义分类变量的取值范围。
单击分类变量按钮,系统弹出一个对话框,如图-3所示。
最小值输入1,最大只输入3.完成设置后,单击继续按钮,返回判别分析主对话框,见图-2.
图-2判别分析的主对话框
图-3指定分类变量范围对话框
3)自变量列表框:
从左侧的变量列表将参与判别分析的变量“X1—X4”于其中,如图-4所示。
4)一起输入变量单按钮:
表示选择所有变量参与判别分析,如图-4所示。
图-4
(4)判别分析的统计输出设置。
单击统计量按钮,系统弹出一个对话框,如图-5所示。
图-5判别分析的统计输出设置
1)描述性框:
描述统计量选项组,包括3个复选框项,复选均值复选框和单变量复选框。
如图-5所示
均值复选框:
各类中个变量的均值、标准差和各自变量总样本的均值、标准差;
单变量复选框:
变量均值的单因子差异假设实验。
2)函数系数框:
判别函数系数选项组,复选Fisher复选框和未标准化复选框,如图-5所示。
Fisher复选框:
给出贝叶斯判别函数的系数。
未标准化复选框:
给出未标准化的Fisher判别函数的系数。
(5)指定判别分析的有关参数及有关输出结果设置。
单击分类按钮,系统弹出一个对话框,如图-6所示。
图-6指定参数与结果对话框
1)先验概率框:
先验概率选项组,包括两个单选项,单选所有组相等框如图-6所示。
所有组相等框:
个二类先验概率相等。
2)输出框:
分类结果选项组,包括三个复选项,复选个案结果、摘要表和不考虑该个案时的分类复选框如图-6所示。
个案结果复选项:
对每个样品输出判别函数值、实际类、预测类和后验概率。
摘要表复选项:
输出分类小结,给出正确分类的样品数、错分样品数和错分率。
不考虑该个案时的分类复选项:
交叉验证的判别分类结果。
3)使用协方差矩阵框:
分类使用的协方差矩阵,单选在组内单选项如图-6所示。
在组内单选项:
使用合并类内协方差矩阵。
4)图框:
复选合并组、分组和区域图复选框如图-6所示。
合并组复选项:
使出包括各个类的散点图。
分组复选项:
每类输出一个散点图。
区域图复选项:
输出领域图。
所有设置完成后,单击继续按钮返回判别分析主对话框。
图-7建立新变量对话框
(6)单击保存按钮,系统弹出一个对话框,复选预测组成员、判别得分和组成员概率复选项如图-7所示。
1)预测组成员复选项:
根据判别函数的值,按后验概率计算预测分类结果。
2)判别得分复选项:
建立判别函数值变量。
3)组成员概率复选项:
建立新变量,表明每一个样品属于某一类的概率。
所有设置完成后,单击继续按钮返回判别分析主对话框。
(7)上述设置完成后,单击确定按钮进行判别分析,得到输出结果。
七、模型的结果
(1)描述性输出
分析案例处理摘要
未加权案例
N
百分比
有效
15
100.0
排除的
缺失或越界组代码
0
.0
至少一个缺失判别变量
0
.0
缺失或越界组代码还有至少一个缺失判别变量
0
.0
合计
0
.0
合计
15
100.0
图-8
图-8表示有效样本及样本变量的实际情况。
组均值的均等性的检验
Wilks的Lambda
F
df1
df2
Sig.
x1
.888
.758
2
12
.490
x2
.426
8.074
2
12
.006
x3
.442
7.564
2
12
.007
x4
.786
1.633
2
12
.236
图-9
由图-9可知显著水平X2、X3最大,而X1、X4显著水平最小。
但是由于判别变量间可能相互关联,仅单独检验是不够的。
但是通过将X1和X4分别与X2和X3联合后发现,他们对判别的提高有很大的贡献。
组统计量
类型
均值
标准差
有效的N(列表状态)
未加权的
已加权的
1
x1
188.6000
57.13843
5
5.000
x2
150.4000
16.50152
5
5.000
x3
.1380
.05933
5
5.000
x4
.2000
.13323
5
5.000
2
x1
163.0000
53.80520
5
5.000
x2
115.0000
14.81553
5
5.000
x3
.0700
.01871
5
5.000
x4
.1360
.07537
5
5.000
3
x1
151.0000
33.80089
5
5.000
x2
121.4000
13.01153
5
5.000
x3
.0500
.01871
5
5.000
x4
.0900
.06782
5
5.000
合计
x1
167.5333
48.47513
15
15.000
x2
128.9333
21.04915
15
15.000
x3
.0860
.05221
15
15.000
x4
.1420
.10094
15
15.000
图-10
上表(图-10)表示各组变量的描述统计情况,给出了各个类型的均值、标准差等统计量。
通过这些数据,可以大致了解3种类型在这4个指标上的差异。
(2)判别函数的检验
特征值
函数
特征值
方差的%
累积%
正则相关性
1
2.768a
93.5
93.5
.857
2
.192a
6.5
100.0
.402
a.分析中使用了前2个典型判别式函数。
图-11
Wilks的Lambda
函数检验
Wilks的Lambda
卡方
df
Sig.
1到2
.223
15.775
8
.046
2
.839
1.847
3
.605
图-12
“特征值”(图-11)表格给出了两个典型判别函数所能解释的方差变异,其中第一个函数解释了所有变异的93.5%,第二个函数解释了余下的6.5%。
因而第二个函数的相对重要性远远小于第一个函数。
“Wilks的lambda”(图-12)表格用来检验各个判别函数有无统计学上的显著意义,根据该表反应的值,这些数据表明,第二个判别函数对判别组仍有显著贡献(犯错概率为60.5%)。
(3)典型判别式函数摘要
标准化的典型判别式函数系数
函数
1
2
x1
.382
.011
x2
.567
-.861
x3
.673
.633
x4
.296
.515
结构矩阵
函数
1
2
x3
.670*
.314
x1
.208*
.178
x2
.673
-.696*
x4
.296
.390*
判别变量和标准化典型判别式函数之间的汇聚组间相关性
按函数内相关性的绝对大小排序的变量。
*.每个变量和任意判别式函数间最大的绝对相关性
图-13
图-14
“标准化的典型判别式函数系数”表格(图-13)是两个判别函数中各个变量的标准化系数,由此可以判断各个函数主要受那些变量的影响;“结构矩阵”(图-14)给出的是判别变量和标准化判别函数之间的相关性数据,同样可以用来判断各个函数受那些判别变量的影响最大。
对于判别函数1,变量X2、X3的判别意义最大,而对判别函数2变量X3、X4的判别意义最大。
(4)未标准化系数和质心函数
典型判别式函数系数
函数
1
2
x1
.008
.000
x2
.038
-.058
x3
17.954
16.880
x4
3.062
5.327
(常量)
-8.204
5.228
非标准化系数
组质心处的函数
类型
函数
1
2
1
2.095
-.053
2
-.873
.505
3
-1.221
-.452
在组均值处评估的非标准化典型判别式函数
图-15图-16
非标准化系数在使用时可以直接通过原始变量进行计算,如图-15所示。
“组质心处的函数”(图-16)表格给出的是各类别的重心在平面上的坐标,如类型一的坐标是(2.095,-0.053).只要根据这里的典型判别函数(未标准化的),计算出每个观测的平面坐标,再计算它们和各类重心的距离,就可以判断其类型归属。
(5)Fisher判别函数
分类函数系数
类型
1
2
3
x1
.127
.104
.101
x2
.715
.569
.611
x3
68.599
24.723
2.328
x4
4.742
-1.376
-7.537
(常量)
-71.993
-43.041
-45.525
Fisher的线性判别式函数
组的先验概率
类型
先验
用于分析的案例
未加权的
已加权的
1
.333
5
5.000
2
.333
5
5.000
3
.333
5
5.000
合计
1.000
15
15.000
图-17
图-18
Fisher判别函数的输出如图-17、图-18所示。
根据分类函数系数表格可得出各类型的Fisher判别函数为:
将某待诊者的四项生化指标分别带入到上述各类型对应的Fisher判别函数,得到三个对应的Fisher函数值,根据Fisher后验概率最大这一判别规则,即所得函数值最大,可以判断某待诊者所属的类型。
(6)典型判别的散点图
图-19
图-20
图-21
以上三图给出的是胃癌、萎缩性胃炎、非胃病三种类型的判别函数值的散点图。
第一个图形表示将类型1,即胃癌的5个样本分别代入两个典型判别函数,得到5对判别函数值,从而构成散点图,其中,横坐标是第一典型判别函数值,纵坐标是第二典型判别函数值。
在用SPSS软件进行判别分析时,都可以得到类似的判别函数值散点图。
以上三点图比较直观地反映了各组观测的分类情况和各组的重心。
图-22
上图给出了三种类型的典型判别函数值总的散点图,同样是把各类的样品分别代入两个典型判别函数,计算得到15对判别函数值,从而构成这样的散点图,其中,横坐标是第一典型判别函数值,纵坐标是第二典型判别函数值。
从图中可以看出,三种类型在图中有各自的分布领域,说明所建立的判别函数的判别精度不太好。
(7)每个个体的判别结果
按照案例顺序的统计量
案例数目
最高组
第二最高组
判别式得分
P(D>d|G=g)
实际组
预测组
p
df
P(G=g|D=d)
到质心的平方Mahalanobis距离
组
P(G=g|D=d)
到质心的平方Mahalanobis距离
函数1
函数2
初始
1
1
1
.273
2
.994
2.597
2
.005
13.074
2.610
1.474
2
1
1
.369
2
.949
1.994
2
.047
8.020
1.834
1.335
3
1
1
.557
2
.998
1.170
2
.001
14.929
2.709
-.944
4
1
3**
.114
2
.597
4.336
1
.237
6.180
.347
-1.821
5
1
1
.658
2
.999
.838
2
.001
15.461
2.974
-.309
6
2
2
.470
2
.487
1.512
3
.330
2.290
.233
-.033
7
2
2
.475
2
.675
1.487
3
.325
2.950
-1.931
1.113
8
2
3**
.907
2
.516
.196
2
.480
.340
-1.130
-.019
9
2
2
.441
2
.564
1.636
1
.243
3.321
.401
.618
10
2
2
.535
2
.616
1.252
3
.384
2.195
-1.939
.844
11
3
2**
.999
2
.611
.003
3
.383
.936
-.897
.460
12
3
3
.910
2
.664
.188
2
.330
1.585
-.910
-.754
13
3
3
.317
2
.778
2.297
2
.190
5.111
-.356
-1.696
14
3
3
.508
2
.619
1.354
2
.381
2.328
-2.304
-.025
15
3
3
.897
2
.614
.218
2
.386
1.147
-1.639
-.244
交叉验证a
1
1
2**
.000
4
.583
38.067
1
.416
38.741
2
1
2**
.005
4
.913
14.950
1
.059
20.424
3
1
1
.390
4
.997
4.119
2
.001
17.190
4
1
3**
.394
4
.855
4.089
2
.145
7.639
5
1
1
.004
4
.999
15.539
2
.001
30.588
6
2
1**
.148
4
.824
6.774
3
.163
10.019
7
2
2
.521
4
.535
3.225
3
.465
3.502
8
2
3**
.975
4
.566
.489
2
.429
1.044
9
2
1**
.193
4
.918
6.084
3
.059
11.580
10
2
2
.699
4
.507
2.198
3
.492
2.258
11
3
2**
.969
4
.723
.546
3
.267
2.541
12
3
3
.874
4
.601
1.222
2
.388
2.096
13
3
3
.328
4
.612
4.626
2
.280
6.189
14
3
2**
.589
4
.526
2.819
3
.474
3.029
15
3
2**
.631
4
.518
2.577
3
.481
2.726
对初始数据来说,平方Mahalanobis距离基于典则函数。
对交叉验证数据来说,平方Mahalanobis距离基于观察值。
**.错误分类的案例
a.仅对分析中的案例进行交叉验证。
在交叉验证中,每个案例都是按照从该案例以外的所有其他案例派生的函数来分类的。
图-23
上表中的案例数目列,是所有个体的编号。
实际组列是每个个体实际上所在的类型。
在最高组(具有最大分辨率)下的预测组列,是按照计算结果的类型。
可以看到编号4经过判别分析后被判到了第三种类型中,即非胃病;编号8经过判别分析后被判到了第三种类型中,即非胃病;编号11经过判别分析后被判到了第二种类型中,即萎缩性胃炎。
上表中的最高组(具有最大分辨率)下的P(D>d|G=g)列和df列,是在样本属于该类型而判别不是相应类型的条件概率及其自由度。
表中P(D=d|G=g)列是判别样本属于相应类型,而样本确实是相应类型的后验概率。
从表中可以看出后验概率还是比较大的。
表中的最高组下的到质心的平方Mahalanobis距离列,是相应个体距类别重心的马氏距离的平方。
上表中的第二最高组(具有第二