高二数学圆锥曲线复习.docx

高二数学圆锥曲线复习.docx

《高二数学圆锥曲线复习.docx》由会员分享，可在线阅读，更多相关《高二数学圆锥曲线复习.docx（51页珍藏版）》请在冰豆网上搜索。

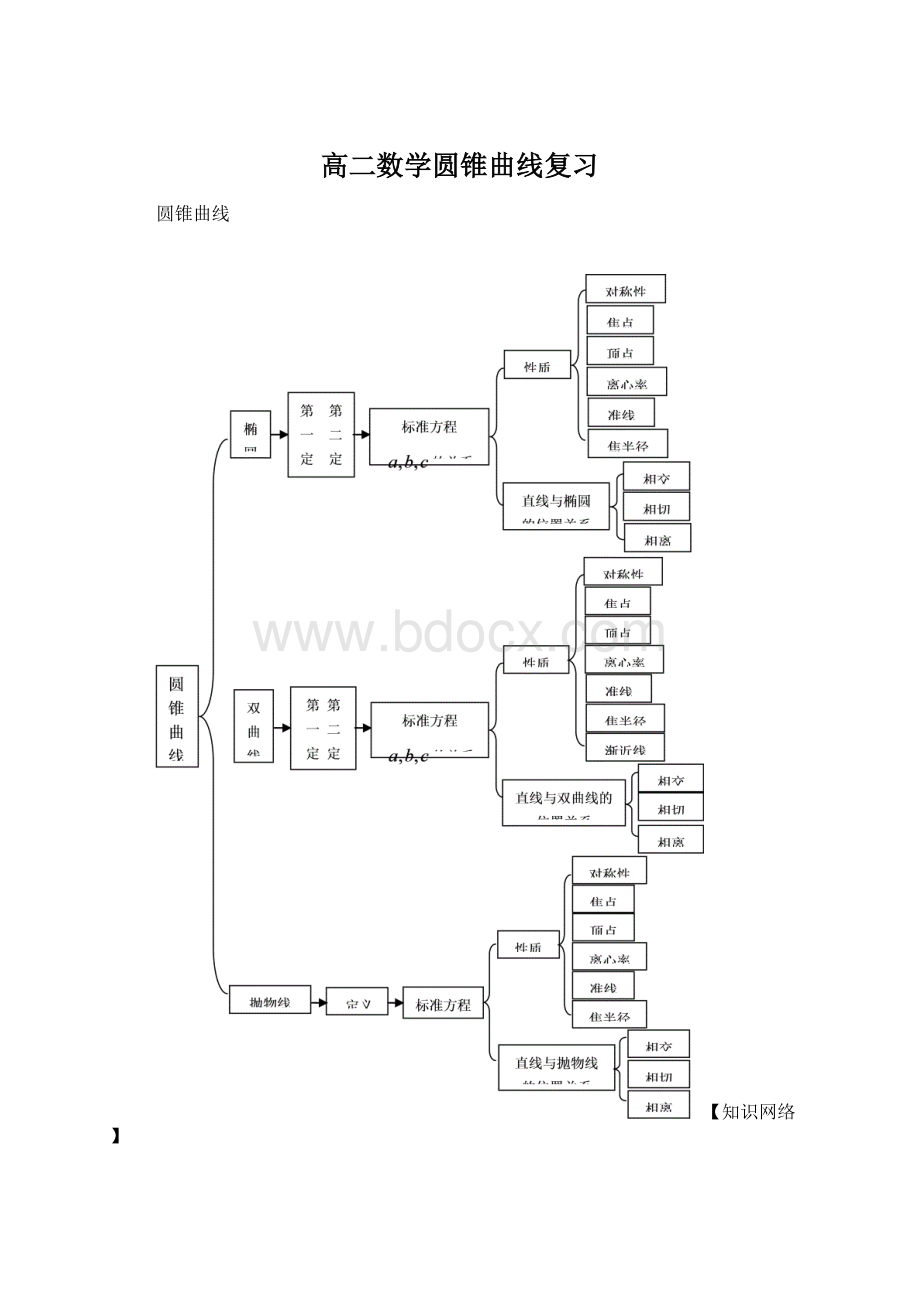
高二数学圆锥曲线复习

圆锥曲线

【知识网络】

3．1椭圆

【考点透视】

一、考纲指要

1．熟练掌握椭圆的定义、标准方程、简单的几何性质及参数方程．

2．考查椭圆的离心率，直线的方程，平面向量的坐标表示，方程思想等数学思想方法和综合解题能力.

二、命题落点

圆锥曲线是解析几何的重点，也是高中数学的重点内容，高考中主要出现三种类型的试题：

①考查圆锥曲线的概念与性质；②求曲线方程和轨迹；③关于直线与圆锥曲线的位置关系的问题，主要考查直线方程,平面向量及椭圆的几何性质等基本知识,考查综合运用数学知识解决问题以及推理能力.

【典例精析】

例1：

（2005·全国1）已知椭圆的中心为坐标原点O，焦点在轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，与共线．

（1）求椭圆的离心率；

（2）设M为椭圆上任意一点，且，证明为定值．

解析:

（1）设椭圆方程为,则直线AB的方程代入,化简得．

令,则．

由与共线,

得　　,又，

．

即,所以，，

故离心率．

（2）由（１）知,所以椭圆可化为

设,由已知得，

在椭圆上,，

即①

由

（1）知，

又代入①，得．

故为定值,定值为1．

例2：

（2005·上海）如图，点、分别是椭圆长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于轴上方，．

（1）求点P的坐标；

（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于，求椭圆上的点到点M的距离的最小值．

解析:

（1）由已知可得点A（－6，0），F（4，0）

设点P的坐标是

，

由已知得

由于

（2）直线AP的方程是

设点M的坐标是（m，0），则M到直线AP的距离是，

于是椭圆上的点到点M的距离d，有

由于

例3：

（2005·福建）已知方向向量为的直线l过点（）和椭圆的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.

（1）求椭圆C的方程；

（2）是否存在过点E（－2，0）的直线m交椭圆C于点M、N，满足cot∠MON≠0（O为原点）.若存在，求直线m的方程；若不存在，请说明理由.

解析:

（1）直线，①

过原点垂直的直线方程为，②

解①②得

∵椭圆中心（0，0）关于直线的对称点在椭圆C的右准线上，

∵直线过椭圆焦点，∴该焦点坐标为（2，0）.

故椭圆C的方程为③

（2）设M（），N（）.

当直线m不垂直轴时，直线代入③，整理得

点O到直线MN的距离．

即

即

整理得

当直线m垂直x轴时，也满足.

故直线m的方程为

或或

经检验上述直线均满足.所以所求直线方程为

或或

【常见误区】

解析几何问题，基本上都与方程思想相结合，因而要注意直线方程与曲线方程联立起来，结合根与系数的关系，或直接解出根，是高考常用的方法，要注意有关方法的练习、归纳，要注意运算的优化，要注意利用数形结合，挖掘隐含性质,这也是考生思维的一个障碍点.

【基础演练】

1．（2005·广东）若焦点在轴上的椭圆的离心率为，则m=（）

A．B．C．D．

2．（2005·福建）设的最小值是（）

A．B．C．－3D．

3．（2005·全国3）设椭圆的两个焦点分别为F1、、F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为等腰直角三角形，则椭圆的离心率是（　　）

A．B．C．　D．

4．（2005·江苏）点在椭圆的左准线上，过点P且方向为的光线经直线反射后通过椭圆的左焦点,则这个椭圆的离心率为

（）

A．B．C．D．

5．（2005·重庆）已知是圆为圆心）上一动点，线段AB的垂直平分线交BF于P，则动点P的轨迹方程为.

6．如图所示,底面直径为的圆柱被与底面成的平面所截，

其截口是一个椭圆，则这个椭圆的长轴长，

短轴长，离心率为．

7．（2005·辽宁）已知椭圆的左、右焦点分别是

、，是椭圆外的动点，满足，

点Ｐ是线段与该椭圆的交点，点Ｔ在线段上，并且

满足．

（1）设为点Ｐ的横坐标，证明；

（2）求点Ｔ的轨迹Ｃ的方程；

（3）试问：

在点Ｔ的轨迹Ｃ上，是否存在点Ｍ，使△的面积．若存在，求∠的正切值；若不存在，请说明理由．

8．（2005·湖南）．已知椭圆C：

＋＝1（a＞b＞0）的左、右焦点为F1、F2，离心率为e.直线l：

y＝ex＋a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设＝λ.

（1）证明：

λ＝1－e2；

（2）若，△PF1F2的周长为6，写出椭圆C的方程；

（3）确定λ的值，使得△PF1F2是等腰三角形.

9．（2005·湖北）设A、B是椭圆上的两点，点N（1，3）是线段AB的中点，线段AB的垂直平分线与椭圆相交于C、D两点.

（1）确定的取值范围，并求直线AB的方程；

（2）试判断是否存在这样的，使得A、B、C、D四点在同一个圆上？

并说明理由.

3．2双曲线

【考点透视】

一、考纲指要

熟练掌握双曲线的定义、标准方程、简单的几何性质．

二、命题落点

1．考查了圆锥曲线中双曲线的渐近线方程与准线方程，以及标准方程中a,b,c之间的关系,两渐近线间的夹角的求法，如例1.

2．双曲线的第一、第二定义在解题中的灵活运用,如例2;

3．考查等边三角形的性质，焦点三角形公式及离心率公式，灵活运用焦点三角形公式避免了繁琐的运算，突出观察研究能力的考查，如例3.

【典例精析】

例1：

（2005·湖南）已知双曲线－＝1（a＞0，b＞0）的右焦点为F，右准线与一条渐近线交于点A，△OAF的面积为（O为原点），则两条渐近线的夹角（）　

A．30º　B．45º　C．60º　D．90º

解析:

双曲线的右焦点F（c,0），右准线方程为x=,一条渐近线方程为y=x，可得点A的坐标（，），△OAF的面积S△OAF=OF│YA│=c=ab,又题意已知S△OAF=a2,所以a=b,两条渐近线间的夹角为900.

答案：

D

例2：

（2005·全国3）已知双曲线的焦点为F1、F2，点M在双曲线上且则点M到x轴的距离为（　　）

A．B．C．D．

解析:

设M到x轴的距离为h，∵，

又∵，

由双曲线定义得，

再由，∴.

答案：

C

例3：

（2005·福建）已知F1、F2是双曲线的两焦点，以线段F1F2为边作正三角形MF1F2，若边MF1的中点在双曲线上，则双曲线的离心率是（）

A．B．C．D．

解析:

令，边MF1交双曲线于点N，连结N易知

答案：

D

例4.（2005·山东）设双曲线的右焦点为，右准线与两条渐近线交于P、两点，如果是直角三角形，则双曲线的离心率.

解析:

如图所示，

且，

在中，

．　　　①

　　②　　　③

将②③代入①式化简得：

答案:

【常见误区】

1．对双曲线离心率、双曲线渐近线等基本知识考察时,应想法利用已知曲线构造等式,从而解出的比值,即双曲线的离心率.这一点考生常不能注意到,致使离心率求解出错,如例3、例4.

2．解题过程中,特别是客观题中,应注意双曲线第一第二定义的应用,此问题考生常会忽视,如例1、例2.

【基础演练】

1．（2006·广东）已知双曲线，则双曲线右支上的点到右焦点的距离与点到右准线的距离之比等于（）

A．B．C．2D．4

2．（2005·天津）设双曲线以椭圆长轴的两个端点为焦点，其准线过椭圆的焦点，则双曲线的渐近线的斜率为（）

A．B．C．D．

3．平面内有两个定点和一动点，设命题甲，是定值，命题乙：

点的轨迹是双曲线，则命题甲是命题乙的（）

A．充分但不必要条件B．必要不充分条件

C．充要条件D．既不充分也不必要条件

4．双曲线和它的共轭双曲线的离心率分别为，则应满足的关系是（　）

A．B．

C．D．

5．（2005·浙江）过双曲线（a＞0，b＞0）的左焦点且垂直于x轴的直线与双曲线相交于M、N两点，以MN为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于_________．

6．（2005·江西）以下几个关于圆锥曲线的命题中：

①设A、B为两个定点，k为非零常数，，则动点P的轨迹为双曲线；②设定圆C上一定点A作圆的动点弦AB，O为坐标原点，若则动点P的轨迹为椭圆；③方程的两根可分别作为椭圆和双曲线的离心率；④双曲线与椭圆有相同的焦点.其中真命题的序号为（写出所有真命题的序号）

7．已知双曲线的左右焦点分别为，左准线为，能否在双曲线的左支上求一点，使是到的距离与的等比中项？

若能，求出的坐标，若不能，说明理由．

8．过双曲线的右焦点作双曲线在第一、第三象限的渐近线的垂线，垂足为，与双曲线的左、右支的交点分别为．

（1）求证：

在双曲线的右准线上；

（2）求双曲线离心率的取值范围．

9．是否同时存在满足下列条件的双曲线，若存在，求出其方程，若不存在，说明理由．

（1）渐近线方程为，

（2）点到双曲线上动点的距离最小值为．

3．3抛物线

【考点透视】

一、考纲指要

掌握抛物线的定义、标准方程和简单的几何性质．

二、命题落点

1．考察抛物线过焦点的性质,如例1;

2．抛物线上张直角问题的探究,考察抛物线上互相垂直的弦的应用，如例2;

3．定值及定点问题是解几问题研究的重点内容,此类问题在各类考试中是一个热点，如例3.

【典例精析】

例1：

（2005·全国3）设两点在抛物线上，是AB的垂直平分线，

（1）当且仅当取何值时，直线经过抛物线的焦点F？

证明你的结论；

（2）当直线的斜率为2时，求在y轴上截距的取值范围.

解析:

（1）∵抛物线，即，∴，

∴焦点为

（i）直线的斜率不存在时，显然有=0;

（ii）直线的斜率存在时，设为k，截距为b,即直线：

y=kx+B．

由已知得：

即的斜率存在时，不可能经过焦点

所以当且仅当=0时，直线经过抛物线的焦点F

（2）设在y轴上截距为b，

即直线：

y=2x+b，AB：

．由得，

∴，且，

∴，

∴．

所以在y轴上截距的取值范围为

例2：

（2005·广东）在平面直角坐标系中，抛物线上异于坐标原点的两不同动点Ａ、Ｂ满足（如图所示）

（1）求得重心（即三角形三条中线的交点）

的轨迹方程；

（2）的面积是否存在最小值？

若存在，请求出

最小值；若不存在，请说明理由．

解析:

（1）∵直线的斜率显然存在，

∴设直线的方程为，

，依题意得

，①

∴，②　③

∵，∴，即，④

由③④得，，∴

∴设直线的方程为

∴①可化为，∴⑤，

设的重心G为，则

⑥，⑦，

由⑥⑦得，即，这就是的重心的轨迹方程．

（2）由弦长公式得

把②⑤代入上式，得，

设点到直线的距离为，则，

∴，

∴当，有最小值，

∴的面积存在最小值，最小值是．

例3：

（2005·江西）M是抛物线上y2=x上的一点，动弦ME、MF分别交x轴于A、B两点，且MA=MB．

（1）若M为定点，证明：

直线EF的斜率为定值；

（2）若M为动点，且∠EMF=90°，求△EMF的重心G的轨迹方程.

解析：

（1）设M（y,y0），直线ME的斜率为k（k>0），

则直线MF的斜率为－k，方程为

∴由，消，

解得，

∴（定值）．

所以直线EF的斜率为定值．

（2）直线ME的方程为

由得

同理可得

设重心G（x,y），则有

消去参数得

【常见误区】

1．运算正确率太低,这是考生在解解析几何问题中常出现的