概率论与数理统计重要公式.docx

概率论与数理统计重要公式.docx

《概率论与数理统计重要公式.docx》由会员分享，可在线阅读，更多相关《概率论与数理统计重要公式.docx（12页珍藏版）》请在冰豆网上搜索。

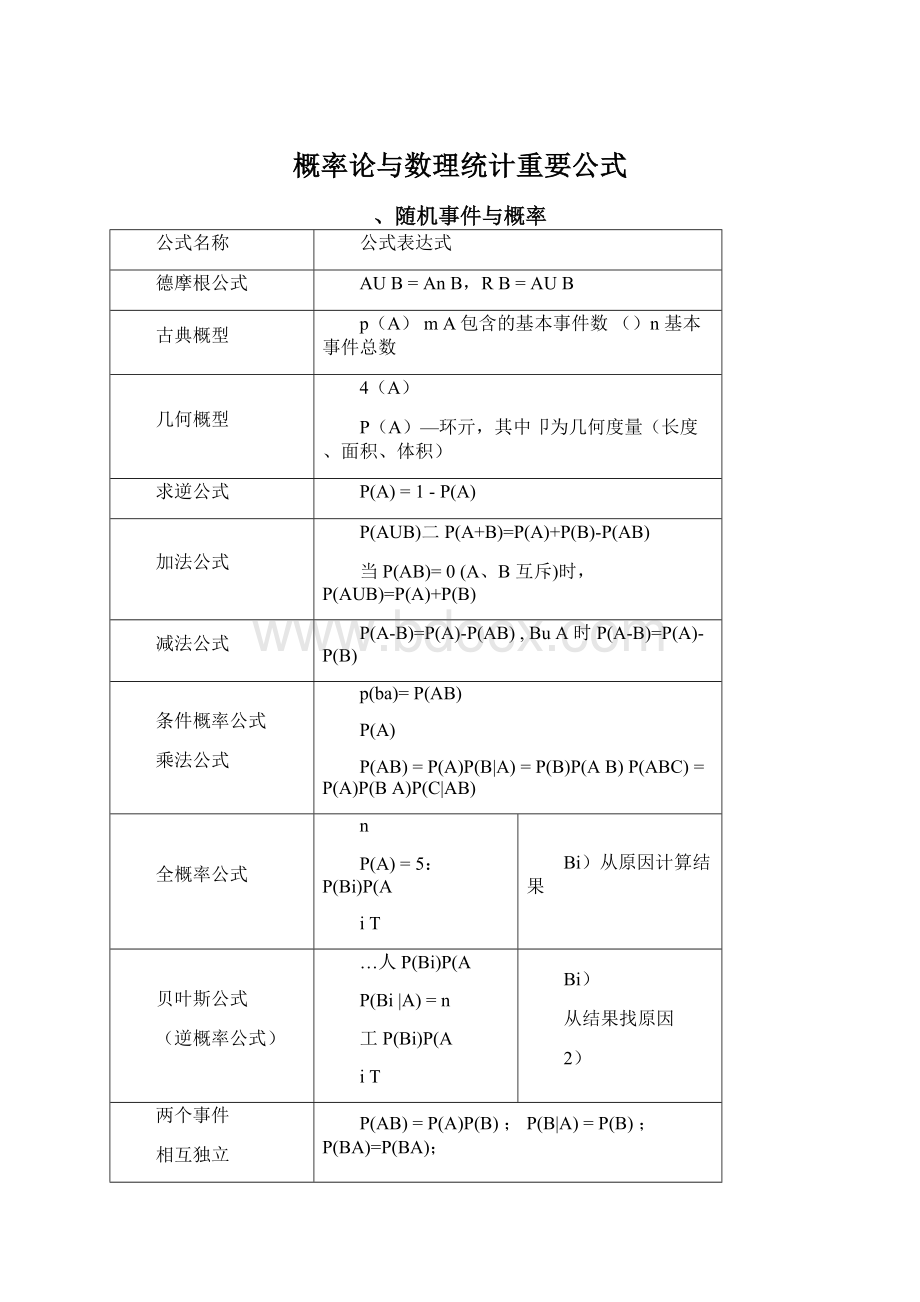
概率论与数理统计重要公式

、随机事件与概率

公式名称

公式表达式

德摩根公式

AUB=AnB，RB=AUB

古典概型

p（A）mA包含的基本事件数（）n基本事件总数

几何概型

4（A）

P（A）—环亓，其中卩为几何度量（长度、面积、体积）

求逆公式

P（A）=1-P（A）

加法公式

P（AUB）二P（A+B）=P（A）+P（B）-P（AB）

当P（AB）=0（A、B互斥）时，P（AUB）=P（A）+P（B）

减法公式

P（A-B）=P（A）-P（AB）,BuA时P（A-B）=P（A）-P（B）

条件概率公式

乘法公式

p（ba）=P（AB）

P（A）

P（AB）=P（A）P（B|A）=P（B）P（AB）P（ABC）=P（A）P（BA）P（C|AB）

全概率公式

n

P（A）=5：

P（Bi）P（A

iT

Bi）从原因计算结果

贝叶斯公式

（逆概率公式）

…人P（Bi）P（A

P（Bi|A）=n

工P（Bi）P（A

iT

Bi）

从结果找原因

2）

两个事件

相互独立

P（AB）=P（A）P（B）；P（B|A）=P（B）；P（BA）=P（BA）；

、随机变量及其分布

'P（x=Xk）

；,P（a：

：

X乞b）=F（b）-F（a）

」（t）dt

2、离散型随机变量及其分布

分布名称

分布律

0-1分布X〜b（1,p）

P（X=k）=pk（1-p）i,k=0,1

二项分布（贝努利分布）

X〜B（n,p）

P（X=k）=Ckpk（1-p）n—k,k=0,1「，n

泊松分布X〜p（人）

k

P（X-k）-e?

k-0,1,2,111

k!

3、续型型随机变量及其分布

分布名称

密度函数

分布函数

均匀分布

x〜U（a,b）

f（x）」

1x

avxcbb-a

0,其他

F（x）■

0,xca

x—a/

a兰xcb

b_a

、1,xZb

指数分布

X〜E（巧

f（x）=

”严,x>0

[0,x兰0

F（x）=丿

1-e~）x,x>0

•0,x兰0

止态分布

x〜N（巴Qj

1-f（x）=f—ev2^▽

—旳

彳（t-円2

1x-2

F（x）=—fe帀dt

V2^=

标准正态分布

x〜N（0,1）

1-竺

®（x）=_e2

-°°

1xJt2

叫F』dt

般正态分布的

概率计算公式

分布函数

对离散型随机变量

对连续型随机变量

a_4II

P（X

:

:

a）

（一）P（X_a）=P（Xa）=U

a

P（aEX乞b）=：

」（b）->（a）

cta

F（x）二P（X乞x）二、P（X=k）

k兰

x

F（x）二P（X乞x）二f（t）dt

分布函数与密度函数的重要关系

F'（x）二f（x）F（x）二P（X乞x）

x

-f（t）dt

4、随机变量函数Y=g（X）的分布

离散型：

P（Y=yj二'Pj,i=1,2,llI，

g（Xj）=y'

连续型：

①分布函数法，

②公式法fY（y）=fx（h（y））h（y）（x=h（y）单调）

h（y）是g（x）的反函数

三、多维随机变量及其分布

1、离散型二维随机变量及其分布

分布律：

P（X二Xi,丫二yj二Pj,i,j=1,2川1联合分布函数F（X,Y）

瓦瓦Pij

xi_xx_y

边缘分布律:

条件分布律:

Pi=P（x=人）二.pijpj二p（y=yj）八Pj

ji

Pi：

P（X=xiY=yj）=,i=1,2,111，P（Y=yjX=Xi）=

Pj

联合密度函数

f（x,y）f（x,y）—0

-be-be

L.」”.J（x,y）dxdy=1

2、连续型二维随机变量及其分布

①分布函数及性质

xy

分布函数：

F（x,y）=_f（u,v）dudv

0乞F（x,y）叮F（x,y）=P{X乞x,Y乞y}

性质：

F（G：

"1,-；jj（x,y）,P（（x,y）"gf（x,y）dxdy

分布函数：

Fx（x）二

y-:

:

FY（y）二f（u,v）dudv

_nO_nO

-Ho

密度函数：

fx（x）「f（x,v）dv

-ho

fY（y）=.f（u,y）du

③条件概率密度

f（x,y）~

fYX（yx）=

-oO

fx（x）'

3、随机变量的独立性

二空也：

:

：

x<:

:

fY（y）

随机变量X、丫相互独立=F（x,y）二Fx（x）FY（y），

离散型：

P{X=i,丫二j}=P{X=i}P{Y=j}Pj二Pi.p.j，连续型

f（x,y）=fx（x）fY（y）

4、二维随机变量和函数的分布（卷积公式）

离散型：

P（Z二zQ二'、P（X二xi,丫二yj）注意部分可加性

连续型：

fz（z）二_f（x,z-x）dx二_f（z-y,y）dy

四、随机变量的数字特征

1、数学期望

E（aX-b）=aE（X）-b，当x、Y相互独立时：

随机变量g（X）的数学期望

②性质：

E（C）=C,E[E（X）]=E（X），E（CX）=CE（X），E（X_Y）=E（X）_E（Y）

E（XY）二E（X）E（Y）（正对逆错）

iJ

2、方差

①定义：

二必护）-[£（七『

2

②性质：

D（C）=0，D（aX士b）=a2D（X），D（X士Y）=D（X）+D（Y）±2Cov（X,Y）当X、Y相互独立时：

D（X-Y）二D（X）D（Y）

3、协方差与相关系数

①协方差：

Cov（X,Y）二E（XY）-E（X）E（Y）,当X、Y相互独立时：

Cov（X,Y）=0

②相关系数：

"爲爲，当X、Y相互独立时」XY=0（X‘Y不相关）

③协方差和相关系数的性质：

Cov（X,X）二D（X）,Cov（X,Y）二Cov（Y,X）

Cov（X1X2,Y）=Cov（X「Y）Cov（X2,Y）,Cov（aXc,bYd）二abCov（X,Y）

Cov（x,a）=0（a为常数）,D（aX_bY）=a2D（X）b2D（Y）_2abCov（X,Y）

4、常见随机变量分布的数学期望和方差

分布

数学期望E（X）

方差D（X）

0-1分布b（1,p）

p

p（1-p）

二项分布b（n,p）

np

np（1-p）

泊松分布P仏）

X

X

均匀分布U（a,b）

a+b

（b-a）

2

12

正态分布N（巴即）

卩

2

CT

指数分布e（^）

1

1

2

nZ.A

五、大数定律与中心极限定理

1、切比雪夫不等式

2D（X）

若E（X）=»,D（X）,对于任意g>0有P{X—E（X）

z

2、大数定律：

①切比雪夫大数定律：

若X

nn

221p1

E（Xi）=#i,D（Xi）=丐且⑴i

②伯努利大数定律：

设nA是n次独立试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则>0,有：

1」号,卩-pv乞=1

3、★中心极限定理

1列维一林德伯格中心极限定理：

独立同分布的随机变量Xi（i=1,2,111），均值为，方差为

▽2>0，当n充分大时有：

Yn=（》Xk-n»）/届_=->n（0,1）

kT/

2棣莫弗一拉普拉斯中心极限定理：

随机变量X〜B（n,p），则对任意x有：

X—npxi

limP{x}-——e^dt=>（x）

np（1-p）二

nh_nP

③近似计算：

P（^Xk^b）—（）-：

-（）

kjJn^Jnu

六、数理统计的基本概念

1、总体和样本的分布函数

n

设总体X〜F（x）,则样本的联合分布函数F（X1，X2…Xn）二i【F（xk）

k

2、统计量

样本均值：

Xi，样本方差：

S2（Xi-X）2=1

nynJ吕

1n_

样本标准差：

S=.（Xi-X）2，样本k阶原点距：

初-—

1n_

样本k阶中心距：

Bk（Xi-X）k,k=1,2,3川

ni二

n一2

、（Xi2—nX）n—1y

1nk

AkXi,k二1,2

ny

3、三大抽样分布

-/2

（1）分布（卡方分布）：

设随机变量X〜B（0,1）（i=1,2,111,n）且相互独立,则称统计量

2=x「x「-x-服从自由度为n的2分布，记为2~2（n）

性质：

①E[2（n）]=n,D[2（n）]=2n②设X~2（m）,Y~2（n）且相互独立，

则XY~2（mn）

⑵t分布：

设随机变量X~N（0,1）,Y~2（n），且X与Y独立，则称统计量

X

自由度为n的t分布，记为T~t（n）

n

性质：

①E（T）=0（n1）,D仃）（n2）

n—2

1

②limh（x）」（x）=e

n一.,2二

2

x

~2

⑶F分布：

设随机变量X~2（m）,Y~2（n），且x与丫独立，则称统计量

F（m,n）

服从第一自由度为m,第二自由度为n的F分布，记为F〜F（m,n）,性质：

设

F~F（m,n），则1F~F（n,m）。

七、参数估计

1.参数估计

①定义：

用巩Xi,X2,L,Xn）估计总体参数「称（Xi,X2丄，Xn）为的估计量,相应的二（X|,X2,川,Xn）为总体V的估计值。

2.点估计中的极大似然估计

设X「X2丄Xn取自X的样本，设X~f（XC）或X~P（XJ），求法步骤：

nn

1似然函数：

L^W.lf（x「）（连续型）或L^W.lP（xD（离散型）

i4i=1

nn

2取对数：

InL（旳八Inf（x.力或InL（力八Tnp/xz）

i4i4

宀r£=f（Xl,X2，川,Xn）

3解方程：

空丄=o,l,虫丄“，解得：

mi

耳"k（Xi,X2,|l（,Xn）

3.估计量的评价标准

估计量的评价标准

无偏性

设0=6（x1,x2,L,xn）为未知参数日的估计量。

右E但）-日，则称$为日的无偏估计量。

有效

性

AAAA

设日1一01（捲必丄,xn）和日2-82（x,,x2,L,xn）是未知参数日的两个无偏估计量。

若D（B1）£D（T2），则称日1比日2有效。

一致性

设日n是日的一串估计量，如寸名＞0，有limPd^n-TK）"则称日n为日的一致wn-^C

估计量（或相合估计量）。

正态总体中，样本均值X是）的无偏估计量

修正样本方差S2是匚2的无偏估计量

5.区间估计单正态总体参数的置信区间

条件

估

计

参数

枢轴量

枢轴量

分布

置信水平为1-a的置信区间

已知

a2

ZX-

N（0,1）

/—CF—CF

x_/〒，x+z/〒1<审27n^2nn丿

未知

2CJ

S/亦

t（n-1）

（-S-S、

「伙心晴”汕一1局

未知

2

2

卡（n-1）S

1一2

CT

仇n—1）

''22、

（n-1）S（n-1）S

未知

2

八町

丿

心n）

rnn

22

送（Xi—4）Z（Xi—4）

i〜i」

京n），心2（门）

1｝

八、假设检验

1.假设检验的基本概念

基本思想

假设检验的统计思想是小概率原理。

小概率事件的概率就是显著性水平a,常取a=0.05,0.01或0.10。

基本步骤

①提出原假设Ho;②选择检验统计量g（X1,L,Xn）；③对于a查表找分位数入，使

P（g（X1丄，Xn）€W）=a，从而定出拒绝域W；

④由样本观测值计算统计量实测值g（xJII,Xn）；并作出判断：

当实测值落入W时拒绝Ho，否则认为接受Ho。

第一类错误：

当Ho为真时，而样本值却落入了拒绝域,应当否定Ho。

弃真错误

P｛拒绝Ho|Ho为真｝=:

第二类错误：

当Hi为真时，而样本值却落入了接受域，应接受Ho。

取伪错误

P｛接受Ho|Hi为真｝=-

2.单正态总体均值和方差的假设检验