3 软件无线电中的信号处理算法及仿真.docx
《3 软件无线电中的信号处理算法及仿真.docx》由会员分享,可在线阅读,更多相关《3 软件无线电中的信号处理算法及仿真.docx(32页珍藏版)》请在冰豆网上搜索。
3软件无线电中的信号处理算法及仿真
第三章 软件无线电中的信号处理算法及仿真
3.1 软件无线电中的正交调制通用模型
软件无线电中的各种调制信号是以一个通用的数字信号处理平台为支撑,利用各种软件来产生的。
每一种调制算法都做成软件模块形式,要产生某种调制信号只需调用相应的模块即可。
而且由于各种调制算法都用软件实现,因此在软件无线电中,可以不断地更新调制模块的软件来适应不断发展的调制体制,具有相当的灵活性、开放性与可发展性。
这里涉及的是信号处理的算法,具体实现可以根据该算法对DSP器件编程。
目前,常用的调制方式分成模拟调制和数字调制。
模拟调制方式有AM,FM,SSB,CW等。
数字调制有ASK,FSK,MSK,PSK,DPSK,QPSK和QAM等。
虽然有如此多的调制方式,但通过对几种调制方式的具体分析后,发现,它们都用到了正交的方法,这样软件无线电中的各种调制完全可以用数字信号处理技术来实现,所以此处称正交调制模型为软件无线电信号调制的通用模型。
。
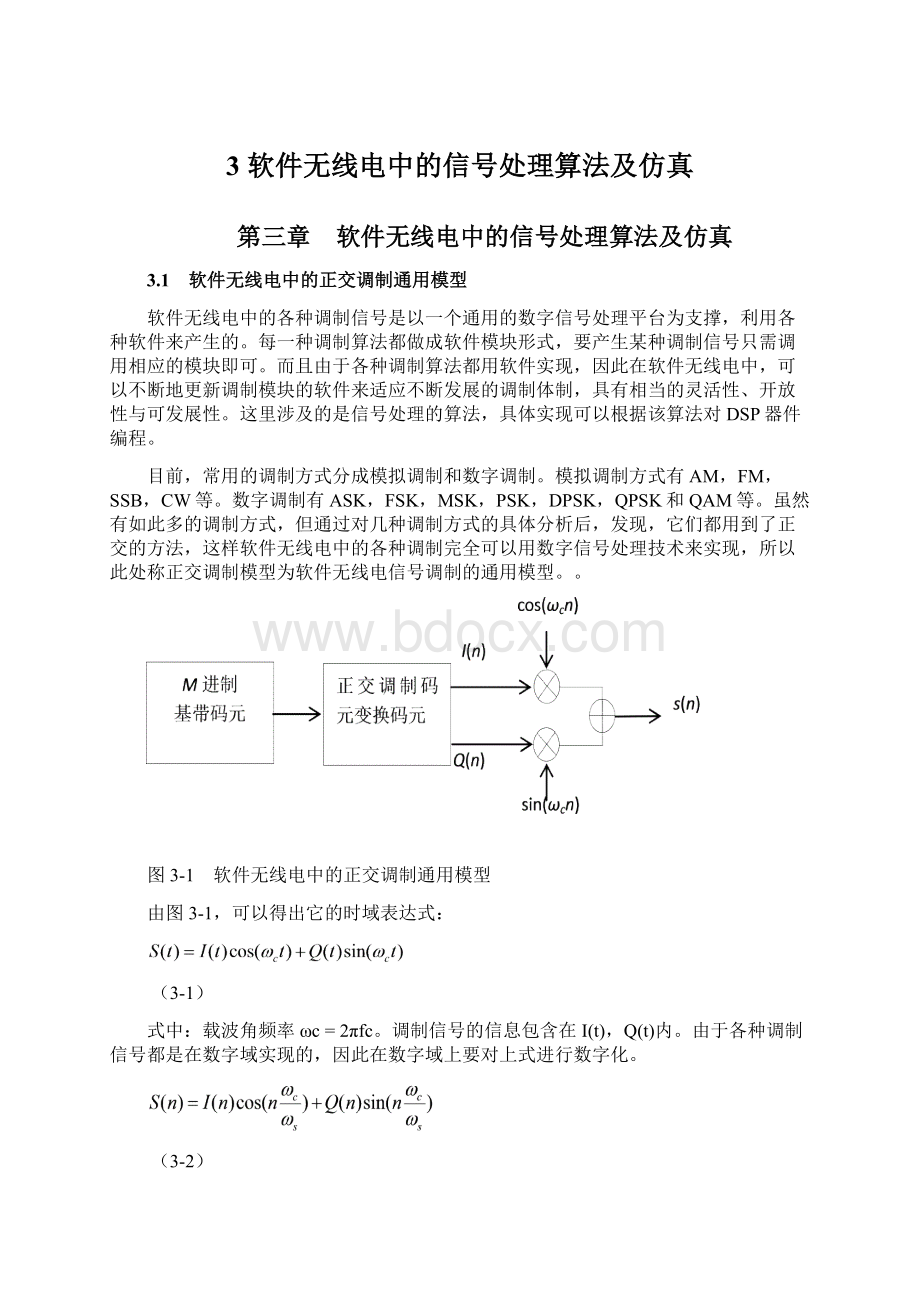
图3-1 软件无线电中的正交调制通用模型
由图3-1,可以得出它的时域表达式:
(3-1)
式中:
载波角频率ωc=2πfc。
调制信号的信息包含在I(t),Q(t)内。
由于各种调制信号都是在数字域实现的,因此在数字域上要对上式进行数字化。
(3-2)
ωs为采样频率的角频率。
下面先对几种信号进行简单的讨论,并给出正交调制的实现方法,最后分别给出MATLAB仿真的调制信号的波形图以及功率谱密度图。
3.2模拟信号的调制算法
1.调幅(AM)
调幅就是使载波的振幅随调制信号的变化规律而变化。
设载波信号为A0cos(ωct+θc),调制信号为f(t),则产生的调幅信号为:
SAM(t)=[A0+f(t)]cos(ωct+θc)
将f(t)=Amcosωmt代入,得
SAM(t)=[A0+Amcosωmt]cos(ωct+θc)
如果将载波信号振幅A0提出,则可得,
SAM(t)=A0[1+βAMcosωmt]cos(ωct+θc)
其中βAM=Am/A0称为调制指数,范围在(0~1)之间,若βAM>1,称为过调幅,已调波的包络会出现严重失真。
若要用式(5-6)用上一节讨论的通用正交模型来替代,则可令
I(t)=A0[1+βAMcosωmt]
Q(t)=0
为了方便起见,可设θc为0。
若将式(5-6)数字化,可得
SAM(n)=A0[1+βAMcosnfm/fs]cos(nfc/fs)(3-3)
最终根据式(3-3)可进行编程。
2.调频(FM)
调频是载波的瞬时频率随调制信号成先行变化的一种调制方式。
设ωFm(t)=ωc+KFmf(t),其中KFm为频移常数。
θ(t)=ωct+KFm∫f(t)dt,则调频信号的时域表达式为:
SFM(t)=Acos[θ(t)]=Acos(ωct+KFm∫f(t)dt)
把上式展开并化简
SFM(t)=Acos(ωct)cos(KFm∫f(t)dt)-Asin(ωct)sin(KFm∫f(t)dt)
=Acos(ωct)cosφ-Asin(ωct)sinφ(3-4)
其中φ=KFm∫f(t)dt。
若要套用通用正交模型,则
I(t)=cosφ
Q(t)=sinφ
从式(3-4)中可见调频的算法比调幅要稍微复杂些,因为需要牵涉到积分运算。
较为严密的处理方法是运用数值求积分方法,它包括机械求积分和插值求积分。
机械求积分中有梯形公式,矩形公式,龙贝格算法等,插值求积分中包括插值求积公式,牛顿柯特斯公式和复化求积公式等等。
在这些算法中,复化求积的算法具有精度高,运算量小,容易得到各样点的积分值等优点。
以下简单介绍。
复化积分法是将求积空间[a,b]分成n等份,步长为h=(b-a)/n,分点为Xk=a+kh,k=0,1~n。
先求各自区间上的积分值Ik,然后再求和。
复化梯形公式为
Tn=∑h[f(k)+f(xk+1)]/2,k=0~n-1(3-5)
采用复化求积公式后,FM的离散数学表达示如下:
SFM(n)=cos[ωcnTs+KFMTs∑[x(iTs)+x[(i-1)Ts]]/2],I=1~n(3-6)
其中Ts为步长(采样时间间隔),相当于式(3-5)中的h,再将式(3-6)展开就是最终的算法表达式。
在实际设计中,为了简单起见,考察调制信号为单音信号,可假设f(t)=cos(ωmt),则表示成
SFM(t)=Acos[ωct+βFMsinωmt]
其中βFM为调频指数=KFmAm/ωm。
上式的数字化形式为
SFM(n)=Acos[nfc/fs+βFMsinnfm/fs](3-7)
最后可根据式(3-7)进行编程。
3.双边带信号(DSB)和单边带信号(SSB)
双边带信号是由调制信号和载波直接相乘得到的,它只有上下边带分量,没有载波分量,如对DSB信号进行滤波,滤除其中一个边带就可以实现单边带调制。
所以DSB信号的时域表达示可以为:
S(t)=f(t)cosωct
处理方法和调幅信号一样,将f(t)用单音展开,再进行数字化即可。
此时可得出:
I(t)=f(t)
Q(t)=0
SSB信号是通过滤除双边带信号的一个边带而得到的。
滤除其上边带就是LSB信号,滤除其下边带就可得到USB信号。
由于单边带信号的频谱宽度仅为双边带信号的一半,一方面可以为日益拥挤的短波频段节约频率资源,另一方面,单边带只传送携带信息的一个边带功率,因而在接收端获得同样信噪比时,单边带能大大节省发射功率。
所以短波频段广泛使用单边带传送信息。
下面给出LSB和USB的时域表达示:
SLSB(t)=(Am/2)cos(ωc-ωm)t
=(Am/2)cosωctcosωmt+(Am/2)sinωctsinωmt(3-8)
SUSB(t)=(Am/2)cos(ωc+ωm)t
=(Am/2)cosωctcosωmt-(Am/2)sinωctsinωmt(3-9)
对(3-8)、(3-9)分别进行数字化后即可实现最终算法。
3.3 几种数字调制技术及其信号特征
1.二进制数字振幅键控(2ASK)
(1)2ASK原理及其实现方法
二进制数字振幅键控是一种最基本的数字调制方式,也是各种数字调制的基础,记作2ASK(BinaryAmplitudeShiftKeying)。
2ASK信号可以表示为一个单极性脉冲与一个正弦载波相乘,即:
(3-10)
式中g(t-nT)是持续时间为T的矩形脉冲,acn为信源给出的二进制符号0,1。
如果令
(3-11)
则
(3-12)
因此,要实现正交调制,只要令I(t)=0
Q(t)=m(t)
就可以实现2ASK调制。
2ASK的时域波形图如图3-2。
图3-2 2ASK信号波形及功率谱密度图
(2)2ASK信号的功率谱及带宽
2ASK的功率谱密度图如图3-2所示。
2ASK的功率谱表达式可以写为
(3-13)
2ASK的功率谱由连续谱与离散谱两部分组成,其中连续谱取决于g(t)经线性调制后的双边带谱,而离散谱则由载波分量确定。
因为2ASK信号的功率谱密度Pe(f)是相应的单极性数字基带信号功率谱密度Ps(f)形状不变地平移至±fc处形成的,所以2ASK的功率谱密度由连续谱与离散谱两部分组成。
它的连续谱取决于数字基带信号的频谱G(f);离散谱是位于±fc处一对频域冲击函数,这表明了2ASK信号中存在着可作载频同步的载波频率fc的成分。
2ASK信号的带宽B2ASK是单极性数字基带信号带宽Bg的两倍。
当数字基带信号的基本脉冲是矩形非归零脉冲时,Bg=1/Tb。
则2ASK信号的带宽B2ASK为:
B2ASK=2Bg=2/Tb=2rs
式中rs为系统的码元速率rs=1/Tb。
2ASK系统的频带利用率为
rB=(1/Tb)/(2/Tb)=rs/2rs=1/2(b/s·Hz)
这表明用2ASK方式传送码元速率为rs的数字信号时,要求该系统的带宽至少为2rs(Hz)。
由此可见,2ASK的频带利用率低,即在给定信道带宽的条件下,它的单位频带内所能传送的数码率较低。
(3)2ASK信号的特点
2ASK信号的主要优点是易于实现,其缺点是抗干扰能力低,主要应用在低速率数据传输中。
2.多进制数字振幅键控(MASK)
(1)MASK原理及其实现方法
多进制数字振幅键控又称为多电平调制。
M进制数字振幅键控信号中,载波振幅有M种取值,每个符号间隔Tb内发送一种幅度的载波信号,其结果是由多电平的数字基带矩形脉冲序列对余弦载波进行振幅调制而成。
M进制数字振幅键控信号MASK信号可表示为:
(3-14)
式中g(t-nT)是持续时间为T的矩形脉冲,acn为信源给出的M进制符号0,1,...,M-1。
MASK信号调制与2ASK调制类似。
M电平的MASK信号S(t)可以看作由振幅互不相等、时间上互不相关的M个2ASK信号叠加而成。
4ASK信号的时域波形图如图3-3。
图3-3 4ASK信号波形及功率谱密度图
(2)MASK信号的功率谱及带宽
2ASK的功率谱密度图如图3-3所示。
根据上面所述可知,MASK信号的功率谱与2ASK信号的功率谱完全相同,它是由M个2ASK信号的功率谱叠加而成,即MASK信号的带宽也可表示为BMASK=2rs。
其中rs为系统多进制码元速率rs=1/Tb。
与2ASK信号相比较,但二者码元速率相等时,两者带宽相等,即:
BMASK=B2ASK。
但频带利用率,rB=Mrs/BMASK=Mrs/2rs=M/2(b/s·Hz)
它是2ASK系统的M倍。
说明在信息速率相等的情况下,MASK系统的频带利用率高于2ASK系统的频带利用率。
(3)MASK信号的特点
a.传输效率高。
与2ASK信号相比,二者码元速率相等时,MASK的信息速率比2ASK的高,是后者的k=log2M倍;二者信息速率相等时,MASK的频带利用率是2ASK系统的k=log2M倍。
b.抗衰落能力差。
因此只宜在恒参信道(如有线信道)中使用。
c.在接收机输入平均信噪比相等的情况下,MASK系统的误码率比2ASK系统的要高。
d.电平数越大,设备越复杂。
3.二进制数字频移键控(2FSK)
(1)2FSK原理及其实现方法
数字频率键控又称频移键控FSK(FrequencyShiftKeying),二进制频移键控记作2FSK。
2FSK信号是用符号0对应载波角频率ω0,符号1对应载波角频率ω1的已调波形。
它可以用一个矩形脉冲对一个载波进行调频实现,其表达式为:
(3-15)
式中a取值为1,g(t-nT)为矩形脉冲,T为码元周期。
ωn取值为ω0,ω1。
2FSK的时域波形图如图3-4。
图3-4 2FSK信号波形及功率谱密度图
(2)2FSK信号的功率谱及带宽
2FSK信号的功率谱也是由连续谱与离散谱构成,其中连续谱由两个双边带谱叠加而成,离散谱出现在两个载波的位置上。
2FSK信号所需最小带宽为B2FSK=|f2–f1|+2rb。
式中rb是基带信号的码元速率,基带信号的带宽为2rb。
h=|f2–f1|/rb为偏移率,即调制指数(或频移指数)。
由于2FSK调制属于非线性调制,所以其频谱特性数学分析比较复杂,这里只给出2FSK的功率谱密度图,如图3-4所示。
(3)2FSK信号的特点
由上面所述2FSK信号最小带宽B2FSK=|f2–f1|+2rb明显比2ASK系统的要大。
因此,从频带宽度或频带利用率上看,2FSK表现最差。
但在2FSK系统中,不需要人为地设置判决门限,它是直接比较两路解调输出的大小来作出判决。
所以在衰落信道中传输数据时,2FSK被广泛使用。
2FSK调制是数字通信中应用较多的一种方式。
在话带内进行数据传输时,国际电报电话咨询委员会(CCITT)推荐在低于1200bit/s数据率时使用2FSK方式。
4.多进制数字频移键控(MFSK)
(1)MFSK原理
MFSK是2FSK的直接推广。
其信号数学表达式为:
(3-16)
式中ωn(n=0,1,...,M-1)为与an相对应的载波角频率偏移。
在实际使用中,通常有ω0=ω1=ωM-1=2rs。
4FSK的时域波形图如图3-5所示。
(2)MFSK信号的功率谱及其带宽
MFSK的功率谱密度图如图3-5所示。
键控法产生的MFSK信号,其相位是不连续的。
设MFSK信号码元速率为rs,即码元宽度为T=1/rs,则MFSK信号的带宽为:
BMFSK=|fmax–fmin|+4rs
其中fmax为最高频率,fmin为最低频率。
由上式易知MFSK信号(M>4)的频带利用率比2FSK信号的要低,且总是低于ASK信号的频带利用率。
(3)MFSK信号的特点
MFSK信号的主要缺点是信号频带宽,频带利用率低。
MFSK一般用于调制速率(载频变化率)不高的短波、衰落信道上的数字通信。
MFSK信号码元加宽后可有效减少由于多径效应造成的码间串扰的影响,从而提高衰落信道上的抗干扰能力。
图3-5 4FSK信号波形及功率谱密度图
5.二进制数字相移键控(2PSK或BPSK)
(1)2PSK原理及其实现方法
数字相位调制又叫相移键控PSK(PhaseShiftKeying)。
二进制相移键控记作2PSK或BPSK。
PSK是利用载波振荡相位的变化来传送数字信息的,其中又分为绝对相移PSK和相对相移DPSK两种。
由于DPSK与PSK以波形形式来看是完全一样的,所以本课题研究只考虑PSK的识别。
2PSK信号形式一般表示为:
(3-17)
式中a取值为1,g(t-nT)为矩形脉冲,T为码元周期。
φn取值为±π/2,分别对应着二进制符号0,1。
2PSK的时域波形图如图3-6所示。
图3-6 2PSK信号的波形及功率谱密度图
(2)2PSK信号的功率谱及带宽
2PSK的功率谱密度图如图3-6所示。
2PSK信号的频谱成分与2ASK信号的相同,也是由连续谱与离散谱构成。
当基带脉冲幅度相同时,其连续谱的幅度是2ASK连续谱幅度的4倍。
当双极性基带信号以相等的概率出现时,没有离散谱分量。
2PSK信号的带宽为B2PSK=2rs。
与2ASK信号一样,是码元速率的两倍。
(3)2PSK信号的特点
2PSK、2DPSK系统在抗噪声性能及频带利用率等方面比FSK与ASK系统优越。
因而广泛应用于数字通信中。
在话带内以中速率传输数据时,2DPSK是CCITT建议选用的一种调制方式。
6.多进制数字相移键控(MPSK或QPSK)
(1)MPSK原理及其实现方法
多进制数字相移键控是利用载波的多种不同相位(相位差)来传送数字信息的调制方式。
和二相调制一样,多进制数字相移键控也可以分为绝对移相和相对(差分)移相两种。
这里只讨论四相绝对相移键控4PSK(或QPSK)。
其一般表达式为:
(3-18)
式中,φn是受信息控制的相位参数,取值为四种相位之一,0,π/2,π,3π/2或者1π/4,3π/4,5π/4,7π/4。
把上式进一步化简可得:
由此,只要令:
就可以实现4PSK调制了。
4PSK信号的时域波形图、功率谱密度图如图3-7所示。
图3-7 4PSK信号的波形及功率谱密度图
7.多进制正交振幅调制(QAM)
(1)QAM原理及其实现方法
由上面MASK与MPSK系统的分析可以看出,在系统带宽一定的条件下,多进制调制的信息传输速率比二进制的高,也就是说,多进制调制系统的频带利用率高。
但这是通过牺牲功率利用率来换取的。
因为随着M值的增加,在信号空间中个信号点间的最小距离减少,相应的信号判决区域也随之减少。
因此,当信号受到噪声和干扰的损害时,接收信号错误概率也将随之增大。
振幅相位联合键控APK(Amplitude-PhaseKeying)调制方式就是为了克服上述问题而提出来的。
在这种调制方式中,当M较大时,可以获得较好的功率利用率,同时利用基于软件无线电的通用正交调制模型也能容易的实现。
正交振幅调制是APK调制方式的一种。
16进制的正交振幅调制记作16QAM(QuadratureAmplitudeModulation),其信号分布图(星座图)如图
3-8所示。
由图可容易看出,16QAM信号可用两个正交调制信号相加而成。
QAM信号的数学表达式为:
(3-19)
式中g(t-nT)是持续时间为T的矩形脉冲,另外:
(3-20)
(3-21)
只要令:
(3-22)
(3-23)
就可以实现QAM调制信号。
16QAM的时域波形图如图3-9所示。
图3-9 16QAM信号的波形及功率谱密度图
(2)16QAM信号的功率谱及带宽
16QAM的功率谱密度图如图3-9所示。
调制过程表明:
QAM信号可以看成是两个正交的抑制载波双边带调幅信号的相加,因此,MQAM与MPSK信号一样,其功率谱都取决于同相和正交基带信号的功率谱。
MQAM与MPSK在相同信号点数时,功率谱相同,带宽均为基带信号带宽的两倍。
(3)16QAM信号的特点
16QAM用16个点的星座位置来代表十六进制的16种数据信号,其信号有12种相位,3种振幅,抗误码能力远大于16PSK信号。
3.4 用于数字调制信号识别的特征参数
特征提取是基于对调制信号的数学分析,从调制信号的功率谱密度、瞬时幅度、瞬时相位及瞬时频率等几方面的信息中提取能用于区分各种调制信号的特征参数。
英国的A.K.Nandi和E.E.Azzouz提出了5个用于数字调制信号识别的特征参数,证明了其有效性,并给出了仿真统计结果。
本课题沿用这5个特征参数,在改进的自动识别流程下,获得了较理想的仿真结果。
下面简要介绍这5个特征参数的定义、原理及判决依据。
3.4.1 瞬时幅度特性
1.中心归一化瞬时幅度功率谱密度的最大值γmax
γmax由式(3-24)定义:
(3-24)
式中N为取样点数,acn(i)为中心归一化瞬时幅度,由下式计算:
(3-25)
(3-26)
(3-27)
式中ma为瞬时幅度a(i)的平均值。
用平均值来对瞬时幅度进行归一化的重要性在于消除信道增益的影响。
γmax表示中心归一化瞬时幅度功率谱密度的最大值,用于FSK信号与其它调制信号的分离。
由于衡包络的FSK信号有稳定的瞬时幅度,所以其中心归一化瞬时幅度为零。
因此其功率谱密度也为零,既不带有任何幅度信息。
PSK信号具有幅度信息是由于受信道带宽的限制,在相位变化时刻将会产生幅度突变,所以会有幅度信息被添加在连续的符号间。
而ASK信号与QAM信号由于本身就具有幅度信息。
而且由于ASK信号与QAM信号有较小的频谱占用率,其能量比较集中。
由ASK信号的功率谱密度图就容易看出,能量大量集中在载频处。
假设其判决门限为t(γmax),则有:
γmaxγmax>t(γmax)2ASK,4ASK,2PSK,4PSK,16QAM
2.中心归一化瞬时幅度绝对值的标准偏差σaa
σaa由式(3-28)定义:
(3-28)
式中acn(i)是中心归一化瞬时幅度,前面已给出它的定义式。
acn(i)主要用于区分2ASK信号和4ASK,16QAM信号。
因为对于2ASK信号其瞬时幅度绝对值是一常数,不含幅度信息,所以从理论上有σaa=0。
而对4ASK、16QAM信号,其瞬时幅度的绝对值不是常数,仍带有幅度信息,所以σaa≠0。
假设其判决门限为t(σaa),则有:
σaaσaa>t(σaa)4ASK,16QAM
3.4.2 瞬时相位特性
1.非弱信号段中心化瞬时相位非线性分量标准偏差σdp
σdp由式(3-29)定义:
(3-29)
式中ΦNL(i)是经中心化处理后的瞬时相位的非线性分量。
在载波完全同步时,有:
ΦNL(i)=φ(i)–φ0(3-30)
式中
,φ(i)为瞬时相位。
而ta是判断弱信号段的一个幅度判决门限电平,低于此电平门限时,信号的相位对噪声很敏感,会造成较大的相位失真。
C是在数据集合{ΦNL(i)}中An(i)>ta即属于非弱信号值的个数。
σdp表示非弱信号段的中心化瞬时相位非线性分量的标准偏差(Standarddeviationofthenormalizeddirectinstantaneousphaseinthenon-weaksegmentsofthesignals),主要用于识别带有相位信息的2PSK、4PSK与16QAM信号。
FSK信号由于其调制原理,频率调制同样反映为相位的变化,所以也带有直接相位信息。
而ASK信号没有直接相位信息,即σdp=0。
假设其判决门限为t(σdp),则有:
σdpσdp>t(σdp)2PSK,4PSK,16QAM,2FSK,4FSK
2.非弱信号段中心化瞬时相位非线性分量绝对值的标准偏差σap[10]
σap的定义:
(3-31)
式中ΦNL(i)定义如上面所述。
σap表示非弱信号段的中心化瞬时相位非线性分量绝对值的标准偏差(Standarddeviationoftheabsolutevalueofthenormalizedinstantaneousphaseinthenon-weaksegmentsofthesignals),主要用于区分2PSK与4PSK,16QAM。
对于2PSK信号,因为其只有两个相位值,故其中心归一化瞬时相位的绝对值为常数,即不带有相位信息,σap而对于4PSK与16QAM,因为它们瞬时相位分别有四个和六个值,取绝对值后仍带有相位信息,所以其中心归一化瞬时相位的绝对值不为常数[11],σap>t(σap)。
假设其判决门限为t(σdp),则有:
σapσap>t(σap)4PSK,16QAM
3.4.3 瞬时频率特性
在瞬时频率特性方面,用于数字调制信号识别的特征参数为非弱信号段中心归一化瞬时频率绝对值标准偏差σaf。
σaf由式(3-32)定义:
(3-32)
式中fN=fm(i)/rs,fm(i)=f(i)-mf,
,其中rs为数字信号的符号速率,f(i)为信号的瞬时频率,fm(i)为中心归一化后的瞬时频率。
σaf表示中心归一化瞬时频率绝对值的标准偏差(Standarddeviationoftheabsolutevalueofthenormalizedinstantaneousfrequencyinthenon-weaksegmentsofthesignals),主要用于区分2FSK与4FSK信号。
对于2FSK信号,其瞬时频率只有两个值,所以经归一中心化后瞬时频率绝对值是常数,即σaf而对于4FSK信号,由于其瞬时频率有四个值,经归一中心化后瞬时频率绝对值仍带有频率信息。
假设其判决门限为t(σaf),则有:
σafσaf>t(σaf)4FSK