幂函数的图像与性质教案与练习.docx

资源描述

幂函数的图像与性质教案与练习.docx

《幂函数的图像与性质教案与练习.docx》由会员分享，可在线阅读，更多相关《幂函数的图像与性质教案与练习.docx（15页珍藏版）》请在冰豆网上搜索。

幂函数的图像与性质教案与练习.docx

幂函数的图像与性质教案与练习

幕函数的图像与性质

【知识整理】

1、幕函数的定义

一般地，形如）uF（xeR）的函数称为幕函数，其中X是自变量，a是常数.如y=/等都是幕函数，幕函数与指数函数，对数函数一样，都

是基本初等函数.

注意：

中，前面的系数为1,且没有常数项。

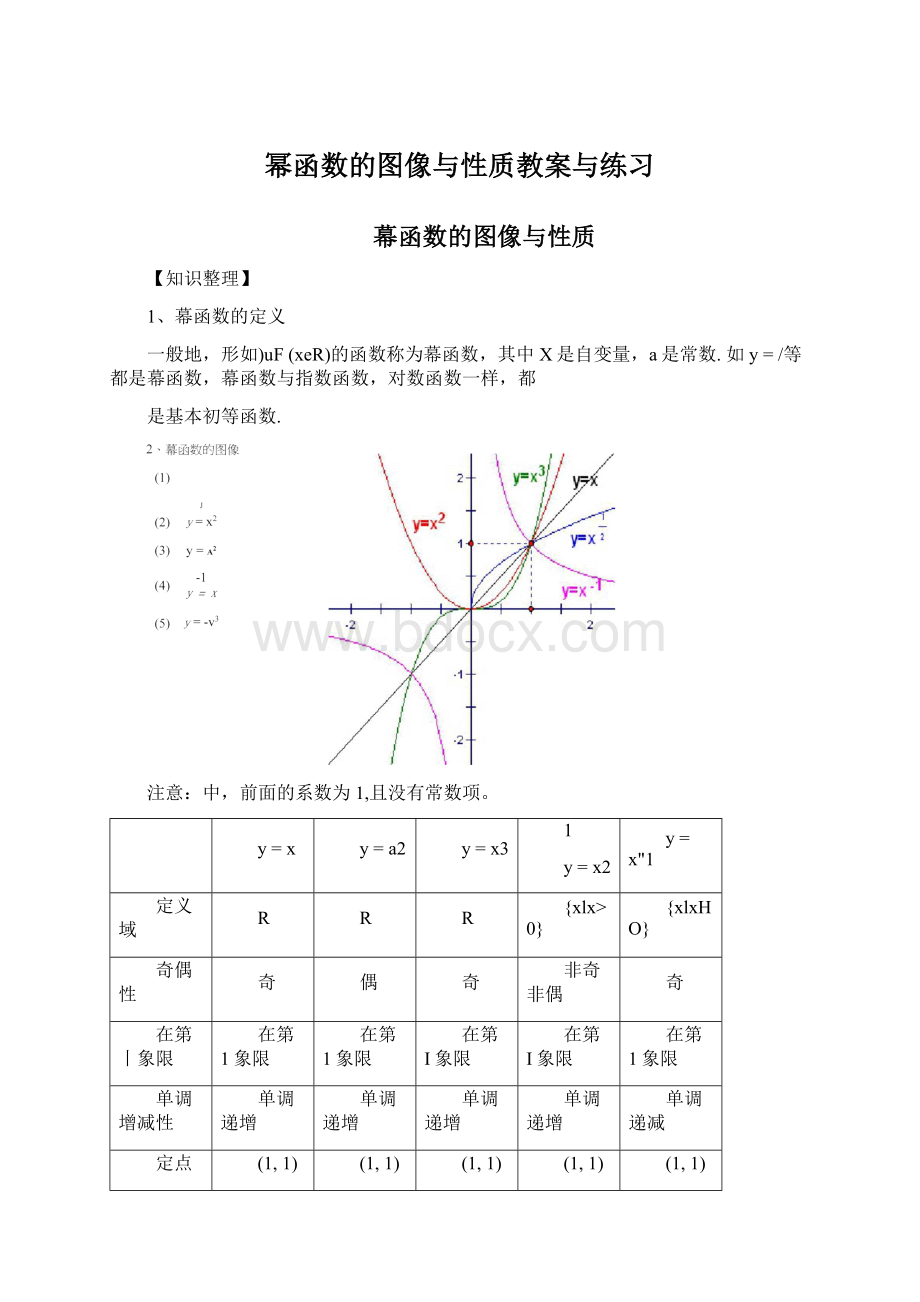
y=x

y=a2

y=x3

y=x2

y=x"1

定义域

{xlx>0}

{xlxHO}

奇偶性

奇

偶

奇

非奇非偶

奇

在第丨象限

在第1象限

在第I象限

在第1象限

单调增减性

单调递增

单调递减

定点

（1,1）

3、幕函数的性质

（1）所有的幕函数在（0,+8）都有定义，并且图象都过点（1,1）（原因：

f=1）；

（2）a>0时，幕函数的图象通过原点，并且在区间［0,+s）上是增函数.特别地,

当a>l时，幕函数的图象下凸；当0vavl时，幕函数的图象上凸；

（3）a<0时，幕函数的图象在区间（0,+s）上是减函数.在第一象限内，当久从右边趋向原点时，图象在y轴右方无限逼近y轴正半轴，当x趋于+oc时，图象在x轴上方无限地逼近x轴正半轴。

基础训练：

1.下列函数是幕函数的是（）

A-y=5ABey=C・y=5x

D.y=（x+l）3

2.已知函数卩=（加2+2加一2）0+2+2〃一3是幕函数，贝ijm=,

n=・

3.已知幕函数f（x）=x°的图象经过点（9,3）,则/（100）=.

4.下列幕函数在（一8,0）上为减函数的是（）

A・y=xB・y=£C.y=x3

D.y=x2

5.下列函数中，定义域为R的是（）

丄

A・y=x~2B・y=x2C・y=x2

D.y=x~l

6.函数y=x3的图象大致是（）

7.下列函数中，既是偶函数，乂在区间（0,+<-）上单调递减的函数是（）

A.y=x_2B.y=x~lC.y=xL

D.y=x3

函数2在区间［*,2］上的值域为

值组成的集合为.

例题精析：

例1.如图，图中曲线是幕函数在第一象限的大致图象.已知a取一2,

一壬，2四个值，则相应于曲线Ci,C2,C3,G的a的值依次为

变式训练：

幕函数）=厂及直线）=兀，）=1,X=1将平面直角坐标系的第一象限分成八个

丄

“卦限”：

①、②、③、④、⑤、⑥、⑦、⑧（如图所示），那么幕函数）=迈的图象经过的“卦限”是・

变式训练：

用“才或y填空:

（3）（-2.1）7（-2.2）-|

例3已知幕函数f（x）=（r—r+1）a1—4/—t2）是偶函数，且在（0,+®）上为增函数，求函数解析式.

变式训练：

若函数ZU）=（〃,一〃?

一1）人厂〃小是幕函数，且在x^（0,+8）上是减函数，求实数加的取值范围.

课后作业：

1一2?

设

1.若幕函数/（X）的图象经过点（2,k则4）=

3},则使幕函数y=xu的定义域为R的所有a的值为

3.幕函数y=/W的图象经过点（2,右），则满足妙=一27的兀值等于

4.函数y=ax~2{a>0且“H1,—1EW1）的值域是[一|,1],则实数a=

7.已知函数＞'=x3.

（1）求定义域；

（2）判断奇偶性;

（3）已知该函数在第一象限的图象如图所示，试补全图象,图象确定单调区间.

&已知幕函数〉=卩「9伽丘2）的图象关于y轴对称，且在（0,+呵上函数值随x的增大而减小，求满足@+1）—吳（3—2“）一扌的a的取值范围.

9.点（迈，2）与点（一2,—*）分别在幕函数/（x）,g（x）的图象上，问当x为何值时，有（lg）>g（x）；（2H（x）=g（x）；（3）/（x）

【题目】如果幕函数y=f（x）的图像经过点（2,4）,则f（3）=

【题目】下列命题中，正确命题的题号为

1幕函数的图像都经过点（1,1）

2图像经过点（-1,1）的幕函数是偶函数

3幕函数的图像不经过第四象限

4当,匸0时，函数y二卍的图像是一条直线

5当〃<0时，函数y二卍在定义域内为减函数

【题目】研究幕函数f（X）=Xj的性质

（1）指出/（Q的定义域和值域；

（2）指出并证明/（Q的奇偶性和单调性；

（3）画出/（X）的图像。

【解答】

（1）定义域为壮尺，值域为_ve［0,+oo）

（2）偶函数，在（y,0］单调减，在［0,+Q单调增

（3）

【属性】高三，幕函数的图像与性质，幕函数的图像与性质，解答题，中，分析问题解决问题

【题目】解不等式（x+2P>（l-2x）~

【解答】兀>3或从冷

【属性】高三，幕函数的图像与性质，恒成立，解答题，难，分析问题解决问题

【题目】已知偶函数/（力=严心在（0,+Q上是减函数（其中加为整数）,

（1）求〃？

的值；

（2）若函数A（A）=<4/a）J2+^U）-3-

【解答】

（1）m=l

（2）-3

【课堂反馈】

【属性】高三，幕函数的图像与性质，幕函数的概念，填空题，易，运算

【题目】幕函数/（x）的图像过点（3,0）,则/⑴的解析式是,

【解答】f（x）=xa,图象过点（3,^/27）,3^=^27=3\«=-

【属性】高三，幕函数的图像与性质，幕函数的图像与性质，选择题，易，逻辑思维

【题目】7.下列命题中正确的是（）

A.当a=0时函数y=的图象是一条直线

B.幕函数的图象都经过（0,0）和（1,1）点

C.若幕函数），=対是奇函数，则y=P是定义域上的增函数

D.幕函数的图象不可能出现在第四象限

【解答】D解析：

A中y=x°（"0）图象是一条直线上去掉点（0,1）；B中幕函数y=T当ovO时，图像不经过（0,0）点；C中=X-1不是定义域上

的增函数。

【属性】高三，幕函数的图像与性质，幕函数的图像，选择题，易,逻辑思维

【题目】函数y=x3和y=G图象满足（）

A.关于原点对称B.关于x轴对称

C.关于y轴对称D.关于直线y=x对称

【解答】D

【属性】高三，幕函数的图像与性质，幕函数的图像与性质，解答题，中，运算

【题目】解不等式（x+2p>（l-2xp

【解答】A-e（-2-i）U（^,+oo）

【属性】高三，幕函数的图像与性质，幕函数的图像与性质，解答题，中，分析问题解决问题

【题目】已知幕函数y=（/2-^l）/7+3，_2，：

）（/eZ）为偶函数，且在（0,+QO）上为增函数

（1）求整数/的值；

（2）作出这个幕函数的图像。

【解答】

（1）匸1

（2）

【课堂小结】

1•幕函数的概念:

y*（R为常数,kwQ）

2•幕函数尸"的鹵像与性质

先画出第一象限图像，其它象限山幕函数性质定

【课后作业】

【属性】高三，幕函数的图像与性质，幕函数的图像，填空题，易，逻辑思维

【题目】当。

日一1，£，1，3^1,幕函数y=x°的图象不可能经过第象限.

【解答】当00时，y>0,故不过第四象限

当X0时，go或无意义.

故不过第二象限.综上，不过二、四象限.也可画图观察.

答案：

二、四

【属性】高三，幕函数的图像与性质，基函数的概念，选择题，易，逻辑思维

【题目】y==（*）',y=W,y=F+l,y=（x—l）',y=x,y="（a>1）上述

函数是幕函数的个数是（）

A,0个B1个C2个

【解答】C

【属性】高三，冨函数的图像与性质，幕函数的图像，选择题，易，逻辑思维

【题目】若四个幕函数〉=/在同一坐标系中的图象

如右图，则a、b、c、d的大小关系是（

A.cl>c>b>aB.a>b>c>d

C.d>c>a>bD.a>b>d>c

【解答］B

【属性】高三，幕函数的图像与性质，幕函数的图像，选择题，易，逻辑思维

【题目】函数y=的图象是（）

【解答】A

【属性】高三，幕函数的图像与性质，幕函数的图像与性质，填空题，中，逻辑思维

【题目】幕函数y=gN5,互质）图象在一、二象限，不

过原点，则k.mj!

的奇偶性为・

【解答】〃讥为奇数，"是偶数

【属性】高三，幕函数的图像与性质，需函数的图像与性质，解答题，中，分析问题解决问题

【属性】高三，幕函数的图像与性质，幕函数的概念，解答题，中，运算

【题目】已知函数用）=伽2一加一1）.严，加为何值时，

⑴是正比例函数；

（2）是反比例函数；

（3）是二次函数；

（4）是幕函数・【解答】⑴若fd）是正比例函数，

则一5加一3=1,解得加=—二，

止匕时历■—加一1H0,故m=—~

（2）若現动是反比例函数，则一5也一3=—1,

2八2

则m=_w此时zzf—加一1工0,故m=—t.

（3）若現力是二次函数，则一5也一3=2,

卩m=—1,此时in—m—1H0,故m=—1,

（4）若f（x）是幕函数，则nf—a—l=l9

即m—m—2=0,解得m=2或m=—1.

综上所述，

（1）当加=一呂时，f（0是正比例函数.

（2）当加=一总时，fg是反比例函数.

（3）当加=一1时，f{x）是二次函数.

⑷当m=2或m=—l时，f（*）是幕函数.

【属性】高三，幕函数的图像与性质，幕函数的图像与性质，解答题，难，分析问题解决问题

【题目】函数fix）=2^和g（x）=3的图象的示意图如图所示，设两函数的图象交于点A（x\,yi）9Bg力），且药5・

（1）请指出示意图中曲线C|,C2分别对应哪一个函数？

•']:

卜

（2）若Ale[a,a+1],疋丘2，b+1]，且“，/

£[1,2,3,4,5,6,7,8,9,10,11,12],指出a,b的值，并说明理由；&j

（3）结合函数图象的示意图，判断/（6）,g（6）,/（2011）^（2011）折_

的大小，并按从小到大的顺序排列.尹―

【解答】⑴G对应的函数为g（x）=/G对应的函数为f3=2：

（2）8=1,b=9.

理由如下：

令03==2’一玄，则瞪，疋为函数03的零点,

由于0⑴=1>0,。

（2）=—4〈0,0（9）=29-93<0,0（10）=2‘°一10$>0,则方程0（x）=f（x）~g{x）的两个零点必丘（1,2）,;r：

e（9,10）,因此整数a=l,b=9.

（3）从图象上可以看出，当xi

・°・f（6）〈g（6）.当xX时，f（x）〉g（x）,

・•・g（2011）

・•・f（6）〈g（6）

【题目资源】

【属性】高三，幕函数的图像与性质，幕函数的图像，填空题，易，逻辑思维

【题目】当时，幕函数y二X11的图象不可能经过第象限

【解答】四

【属性】高三，幕函数的图像与性质

展开阅读全文