勒让德函数.docx
《勒让德函数.docx》由会员分享,可在线阅读,更多相关《勒让德函数.docx(24页珍藏版)》请在冰豆网上搜索。
勒让德函数
在特殊函数中的应用
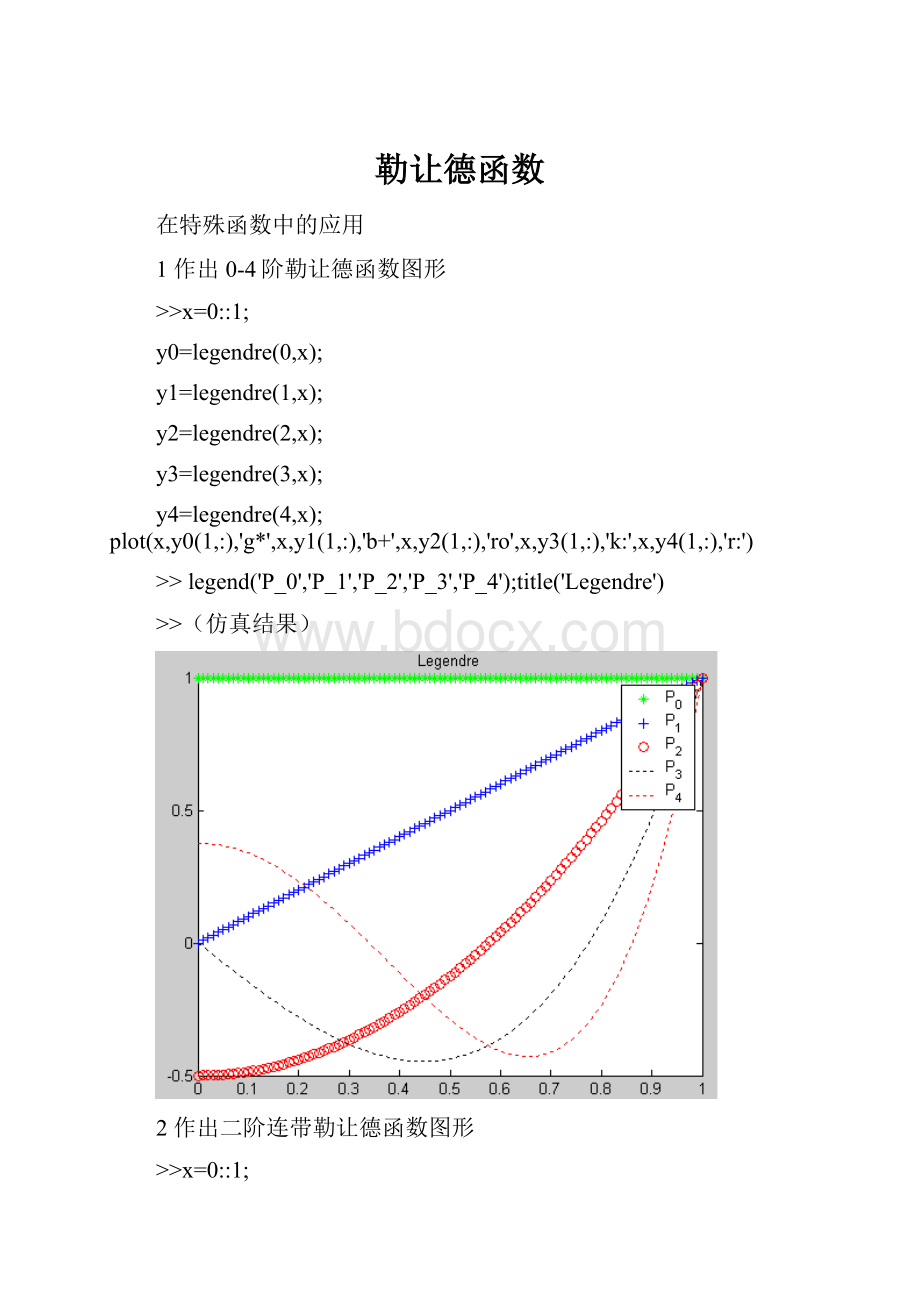
1作出0-4阶勒让德函数图形
>>x=0:
:
1;
y0=legendre(0,x);
y1=legendre(1,x);
y2=legendre(2,x);
y3=legendre(3,x);
y4=legendre(4,x);plot(x,y0(1,:
),'g*',x,y1(1,:
),'b+',x,y2(1,:
),'ro',x,y3(1,:
),'k:
',x,y4(1,:
),'r:
')
>>legend('P_0','P_1','P_2','P_3','P_4');title('Legendre')
>>(仿真结果)
2作出二阶连带勒让德函数图形
>>x=0:
:
1;
y=legendre(2,x);
plot(x,y(1,:
),'g*',x,y(2,:
),'b+',x,y(3,:
),'ro')
>>legend('P_2^0','P_2^1','P_2^2')
3作出三阶连带勒让德函数图形
>>x=0:
:
1;
y=legendre(3,x);
plot(x,y(1,:
),'g*',x,y(2,:
),'b+',x,y(3,:
),'ro',x,y(4,:
),'k:
')
>>legend('P_3^0','P_3^1','P_3^2','P_3^3')
4作出整数阶贝塞尔函数的图形
>>clear
y=besselj(0:
5,(0:
:
10)');
plot((0:
:
10)',y)
ylabel('j_v(x)')
xlabel('x')
legend('J_0','J_1','J_2','J_3','J_4','J_5')
text(1,,'J_0(x)')
text(2,,'J_1(x)')
text(3,,'J_2(x)')
text,,'J_3(x)')
text,,'J_4(x)')
>>text,,'J_5(x)')
Legendre函数
2007年12月13日星期四01:
00
Legendre函数在解圆平台上电势场时必然遇到的,是在极坐标下考察纬度变量时必然会遇到的。
1.氢原子波函数的角度部分:
用MATLAB来画一画:
l=0,m=0,即s轨道角度部分:
t=0:
:
2*pi;
y0n=legendre(0,cos(t),'sch');
polar(t,y0n(1,:
).^2);
l=1,m=0,+1,-1即p轨道角度部分:
t=0:
:
2*pi;
y1n=legendre(1,cos(t),'sch');
polar(t,y1n(1,:
).^2,'r');
holdon;
polar(t,y1n(2,:
).^2,'g');
l=2,m=0,+1,-1,+2,-2即d轨道角度部分:
t=0:
:
2*pi;
y2n=legendre(2,cos(t),'sch');
polar(t,y2n(1,:
).^2,'r');%d(z^2)
holdon;
polar(t,y2n(2,:
).^2,'g');
polar(t,y2n(3,:
).^2,'b');
Legendre多项式
函数
()
由于展开式
()
而称为Legendre(勒让德)多项式的母函数。
展开项系数
称为Legendre多项式,下节将证明它满足Legendre方程式()。
称为阶。
将式()左边利用二项式定理展开,有
在上式中,含有
的项只出现在含
的项和以前各项中。
在这些项中,将含
的各项展成幂级数,并找出所有含
的项,其系数合为
()
其中,
这是因为当
时,求和中最低幂项是
,当
时,最低幂项是
。
Legendre多项式的具体形式写成
()
Legendre多项式的另一微商表达式是Rodrigues(洛德利格)公式
()
()式和()的正确性可以代入Legendre方程式()直接证明。
由式()和()可得出前几阶Legendre多项式具体形式
图显示
在区间〔-1,1〕上的图形,一般有
图Legendre函数
第二类Legendre函数
值得一提的式,Legendre方程()应有另一个独立的解,这个解称为第二类Legendre函数,记为
。
其形式为
等一般的形式是
由于
的对数形式,第二类Legendre函数在边界
是无界的(并非全部
)。
因此不能构成Legendre方程的本征函数系,所以,对
将不在作讨论。
Legnedre多项式的零点
的零点都是一阶的,全部位于区域〔-1,1〕内。
且
与
的零点相互穿插,在
的两个相邻零点之间必有一个
的零点;反之亦然。
Legnedre多项式的性质
Legendre多项式的性质如下:
递推公式
①
②
对称性
③
特殊点的值
④
⑤
⑥
积分表达形式
⑦
Laplace第一积分
⑧
取
,由式()得
取
,由式()得
⑨
Laplace第二积分
⑩
积分公式
()
()
()
利用Rodrigues公式()可证明积分公式,下面证明方程()。
利用式(),有
将积分作
次分部积分,然后设
,并利用积分公式
得
下面由母函数入手,证明Legendre多项式得递推公式,将母函数式()写下
()
对式()两边取
导数,得
用
乘上两边,得
将上式左边中母函数再作展开,得等式
()
比较()式两边项得系数,得递推关系。
这是式()的结果。
同理,对式()两边的求导,得
将上式两边乘以
,并将左边母函数展开,得
()
比较
项的系数,得
这就是式()。
其它递推公式可依此导出,这里不再证明。
利用母函数,已证明Legendre式多项式()满足递推公式()~(),则式()是Legendre方程()的解。
下面证明定理。
定理设函数是
在〔-1,1〕区间上有一、二阶连续倒数的连续函数,
若
满足递推公式()和式()~(),则
是Legendre方程
的解。
将递推公式()两边对
求导,得
()
再将式()乘以
,得
()
将式()乘以
,并与式()相加,得
()
由式(),将
换
成,有
()
将式()两边对
求导,得
()
或写成
()
将式()代入式(),得
()
再由式()将式()中的
项替代,最后,得到Legendre方程
Fourier-Legendre级数
第6章§讨论了区间〔-1,1〕上,Legendre方程的本征值为
()
相应的本征函数是Legendre多项式
()
由Legendre方程()知
,
。
在
边界,
因而Legendre方程的解满足自然边界条件,因而有本征函数正交性
()
第6章§还讨论了函数
在区间〔-1,1〕上用Legendre函数展成的广义Fourier级数,称为Fourier-Lengendre级数。
模计算如下:
将母函数式()两边平方,得
()
Fourier-Lengendre级数展开定理
若在区间〔-1,1〕上连续,或有限第一类间断点,那么,Fourier-Lengendre级数
()
其中
()
()
在〔-1,1〕上的连续点收敛于
;在
的间断点,则收敛于平均值
;在
,收敛于
;在
,级数收敛于
。
将方程()两边对
从-1到1积分,并利用正交关系式()可知式()右边的第二项积分等于零。
于是,有
()
式()左边的积分可完成为
()
将式()与式()的右边相比较,得
【例】在〔-1,1〕区间上,试求
展成Fourier-Lengendre级数。
解设
根据积分公式()可知,当
时,所有积分等于零,即
利用式(),计算得
(被积函数是奇函数)
于是有
由上述计算可得出以下结论:
在的Fourier-Lengendre级数中,若是奇数,只含奇数阶Lengendre多项式;若为偶数,只含偶数阶Lengendre多项式。
且Lengendre多项式的阶数最高阶为。
下面列出部分的Fourier-Lengendre多项式的阶数:
具有轴对称性的物理问题举例
由本章§1的讨论可归纳出具有轴对称性的物理问题的形式解。
把对称轴取作求坐标的轴,Helmholtz方程描写的轴对称问题形式解为
()
Laplace方程描写的轴对称问题的形式解:
对于球内问题,有
对于球外问题,
应为零。
【例】半径为的均匀带电圆环,总电量为
,如图,求圆环周围空间的电势。
图带电的圆环
解先由Coulomb(库仑)定律求在
轴上的电势,
()
将式()作Laurant(罗朗)展开,得
()
势()可看成是形式解()在
的边界条件。
比较两式,且有
,得
【例】半径为的半球导体,球面温度保持在,底面温度保持为,如图,求半导体球内的稳定温度分布。
图半圆形导体
解稳定时,导体内的温度分布满足Laplace方程。
温度分部具有轴对称性。
对于球内问题,由式()有
()
边界条件是
()
()
由式(),有
显然,只有当
为奇数
时才有
。
因而,式()成为
()
由式(),有
利用Fourier-Legendre级数展开定理,有
()
最后一步积分是利用习题第3①题的结果求得的。
将式()换写成
表达式,并代入式(),有
()
§3*连带LEGENDRE多项式
连带LEGENDRE多项式
上节讨论了对称的定解问题,当
时,式()转变成Legendre方程()。
当物理问题是非轴对称时,
将式()写下:
()
类似地,作代换,令
,式()变成连带Legendre方程
()
式()的本征值是
,只有当
取
等整数时,式()才有本征函数解。
设
()
于是,有
将上述结果代入式()得
()
另则,由Legendre方程()对
作
次求导,得
()
比较式()与()有
()
由式()得到满足方程()的连带Legendre多项式
()
在以上推导中,
阶导数表示为
特别是
连带LEGENDRE多项式的性质
积分表达式
①
()
递推公式
②
()
③
④
()
⑤
()
对称性
⑥
()
⑦
()
⑧
()
正交关系
⑨
()
⑩
()