《大学物理》概念.docx
《《大学物理》概念.docx》由会员分享,可在线阅读,更多相关《《大学物理》概念.docx(19页珍藏版)》请在冰豆网上搜索。
《大学物理》概念
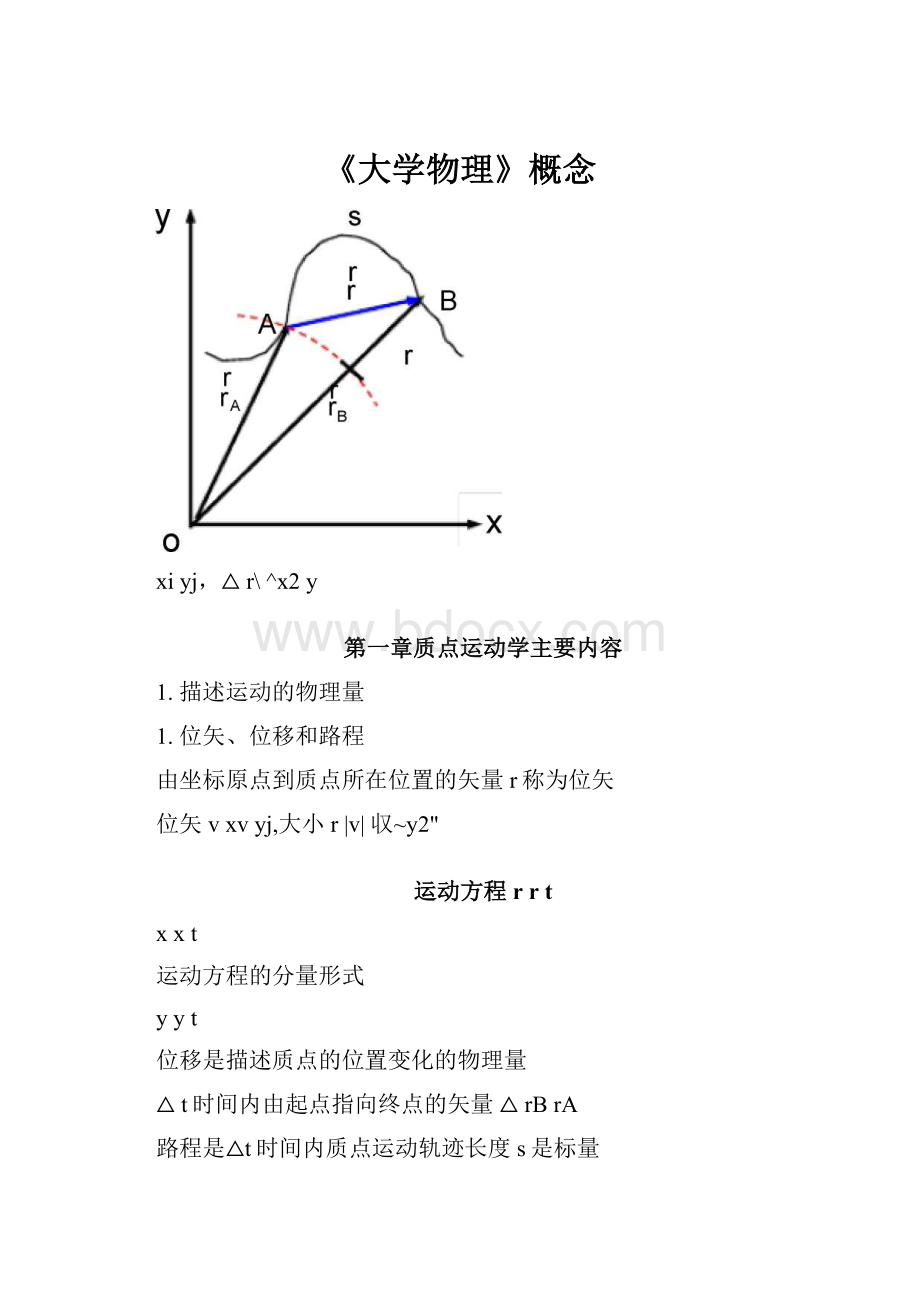
xiyj,△r\^x2y
第一章质点运动学主要内容
1.描述运动的物理量
1.位矢、位移和路程
由坐标原点到质点所在位置的矢量r称为位矢
位矢vxvyj,大小r|v|収~y2"
运动方程rrt
xxt
运动方程的分量形式
yyt
位移是描述质点的位置变化的物理量
△t时间内由起点指向终点的矢量△rBrA
路程是△t时间内质点运动轨迹长度s是标量
明确F、r、s的含义(rrs)
2.速度(描述物体运动快慢和方向的物理量)
平均速度UDt
Dr=Vxr+Dyjr
VtDC=Uxi+Uyj
瞬时速度(速度)v
呱知速度方向是曲线切线方向)
VxiVyj,v
dr
dt
dxdt
2
dy
dt
2
Vy
ds
dt
dr
dt
速度的大小称速率。
3.加速度(是描述速度变化快慢的物理量)
平均加速度a—瞬时加速度(加速度)
t
△叫
r
d
dt
d2r
dt2
a方向指向曲线凹向a2竽
.2,2
dx.dy
2i2dt2dt2
22
axay
2
dVx
dt
dVy2
dt
2222
d2xdy
.dt2dt2
二.抛体运动
运动方程矢量式为
rr1r2rVot-gt
xv0cost(水平分运动为匀速直线运动)
分量式为
12
v0sint-gt(竖直分运动为匀变速直线运动)
y
2
三.圆周运动(包括一般曲线运动)
ds
1.线量:
线位移s、线速度V—
dt
切向加速度at
法向加速度an
2.角量:
角位移
(单位rad)、角速度
知单位rad
s1)
dV(速率随时间变化率)dt
2
即(单位radS2
角速度&
卷(速度方向随时间变化率
第二章牛顿运动定律主要内容
、牛顿第二定律
物体动量随时间的变化率罟等于作用于物体的合外力f
Fi壬即:
rdPdmvF=—
dtdt
r
常量时F
rma
dt
说明:
(1)只适用质点;
(2)F为合力
(3)a与f是瞬时关系和矢量关系;
(4)解题时常用牛顿定律分量式
(平面直角坐标系中)
rrFxmax
FmaFymay(一般物体作直线运动情况)
2
(自然坐标系中)Fma
Fnmanm#-(法向)
(物体作曲线运动)
Ftmatm-(切向)
dt
运用牛顿定律解题的基本方法可归纳为四个步骤
运用牛顿解题的步骤:
1)弄清条件、明确问题(弄清已知条件、明确所求的问题及研究对象)
2)隔离物体、受力分析
对研究物体的单独画一简图,进行受力分析)
3)建立坐标,列运动方程(一般列分量式);
4)文字运算、代入数据
举例:
如图所示,把质量为m10kg的小球挂
在倾角300的光滑斜面上,求
1
(1)当斜面以a1g的加速度水平向右运动时,
3
⑵绳中张力和小球对斜面的正压力解:
1)研究对象小球
2)
隔离小球、小球受力分析
3)建立坐标,列运动方程(一般列分量式)
x:
Ftcos30°Nsin30°ma
(1)
y:
FtSin30°Ncos30°mg0
(2)
4)文字运算、代入数据
x:
、、3FtN2ma(a£g)(3)
y:
Ft、3N2mg(4)
77.3N
11
Ft-mg
(1)一109.81.577
232
mg
cos30°
FT9tg30°
109.8
0.866
77.30.57768.5N
(2)由运动方程,N=0情况
o
y:
Ftsin30=mg
o
a=ggctg30
9.8^317%
x:
Ftcos300ma
第三章动量守恒和能量守恒定律主要内容
1.动量定理和动量守恒定理
1.冲量和动量
rt2v
IFdt称为在t1t2时间内,力F对质点的冲量。
质量m与速度v乘积称动量PmJ
2.质点的动量定理:
1
t2rr
Fgjtmv2
t1
rmw
质点的动量定理的分量式:
Ix
t2
tFxdtmv2xmv1x
彳
Iy
t2
Fydtmv2ymv1y
t1
Iz
h
t2
Fzdtmv2zmv1z
t1
3.质点系的动量定理:
t2nr
Fexdt
t1i
nrnr
mMmiovio
ii
rrPP°
Ix
Px
P
1ox
质点系的动量定理分量式
Iy
Py
Poy
Iz
Pz
Poz
动量定理微分形式,在dt时间内
r
:
Fdt
dP或F二dP
dt
4.动量守恒定理:
当系统所受合外力为零时,系统的总动量将保持不变,称为动量守恒定律
nn「n「
F外=Fi0,贝UmM=mi°Vi0=恒矢量
i1ii
若Fx
0,
则
mMx
G
恒量
动量守恒定律分量式:
若Fy
0,
则
I
I
C2
恒量
若Fz
0,
则
my
C3
恒量
i
2.功和功率、保守力的功、势能
1.功和功率:
一一bvrb
质点从a点运动到b点变力F所做功WFdrFeosds
aa
恒力的功:
WFeosrr
r
功率:
p■dwFeosvFgV
dt
2•保守力的功
一rr
物体沿任意路径运动一周时,保守力对它作的功为零?
Fgdr0
l
3.势能
保守力功等于势能增量的负值,wEpEp0VEp
物体在空间某点位置的势能Epx,y,z
W|ex
W|In
i
mv
2
2
2mv10
11
万有引力作功:
wGMm—
「bra重力作功:
wmgybmgya
弹力作功:
w-kx/-kx^
22
三.动能定理、功能原理、机械能守恒守恒
1.动能定理
11
质点动能定理:
W-mv2-mv^
22
质点系动能定理:
作用于系统一切外力做功与一切内力作功之和等于系统动能的增量
ex
Wnc"
exin
当WWnc0
机械能守恒定律:
只有保守内力作功的情况下,质点系的机械能保持不变
WexW,n(EkEp)(Ek0Epo)
第五章机械振动主要内容
一.简谐运动
振动:
描述物质运动状态的物理量在某一数值附近作周期性变化机械振动:
物体在某一位置附近作周期性的往复运动。
简谐运动动力学特征:
Fkx
简谐运动运动学特征:
a简谐运动方程:
x=Acos(wt+j)
简谐振动物体的速度:
v=空=-wAsin(wt+j)dt
加速度a=密=-w2Acos(wt+j)dt2
速度的最大值Vm=wA,加速度的最大值am=w2A
2.描述谐振动的三个特征物理量
2
1.振幅A:
A=Jx:
+淫,取决于振动系统的能量。
Vw
3.相位wt+j
,它决定了振动系统的运动状态
(x,v)
x00,v00,在第四象限’即取(即2)
3.旋转矢量法简谐运动可以用一旋转矢量(长度等于振幅)的矢端在Ox轴上的投影点运动来描述
rr
1.A的模A二振幅A,
2.角速度大小=谐振动角频率
3.t0的角位置是初相
4.t时刻旋转矢量与x轴角度是t时刻
振动相位t
5.矢端的速度和加速度在Ox轴上的投影点速度和加速度是谐振动的速度和加速度。
4.简谐振动的能量
2
A
以弹簧振子为例:
EEkEp-mv2-kx2-m
p222
5.同方向同频率的谐振动的合成
设XiA-cost-
x2A2cost2
xx1x2Acos(t)
合成振动振幅与两分振动振幅关系为:
AA1A22A1A2cos(21)
A1sin1A2sin2tg—---
A1cos1A2cos2
合振动的振幅与两个分振动的振幅以及它们之间的相位差有关。
2kk012LA从;A2A1A2A1A2
(2k1)k012LA,A2A2A1A2AA2
一般情况,相位差21可以取任意值|A1A2A|A1A2
第六章机械波主要内容
1.波动的基本概念
1.机械波:
机械振动在弹性介质中的传播。
2.波线——沿波传播方向的有向线段。
波面一一振动相位相同的点所构成的曲面
3.波的周期T:
与质点的振动周期相同。
4.波长:
振动的相位在一个周期内传播的距离
5.振动相位传播的速度。
波速与介质的性质有关
2.
质点的振动加速度
2Acos[(t-)]
u
简谐波
沿ox轴正方向传播的平面简谐波的波动方程
yAcos[(tX)
u
]Acos[2(半X)]
质点的振动速度
vyASin[
(t
x
—)
u
这是沿ox轴负方向传播的平面简谐波的波动方程
tx
yAcos2()
3.波的干涉
相遇区域内出现有的
两列波频率相同,振动方向相同,相位相同或相位差恒定,地方振动始终加强,有的地方振动始终减弱叫做波的干涉现象。
两列相干波加强和减弱的条件:
(1)2122k(k0,1,2,)时,AA2
(振幅最大,即振动加强)
212■r2_2k1(k0,1,2,)时,AA1A2
(振幅最小,即振动减弱)
(2)若21(波源初相相同)时,取「2「1称为波程差。
「2「12k(k0,1,2,)时,AA1A2(振动加强)
「2「12k1-(k0,1,2,)时,AA1A2(振动减弱);
其他情况合振幅的数值在最大值A1A2和最小值A1A2之间。
第七章气体动理论主要内容
PVC
PV1
PV2.
J
m
PnkT
PV
RT;
T
T1
T2
M
.理想气体状态方程:
R8.31Jkgmol;k1.381023Jk;Na6.0221023mol1;RNa*
2.理想气体压强公式
21~2
p-n匚_kt-mv分子平均平动动能
32
3.理想气体温度公式
匚1mv23kT
22
4.能均分原理
1.自由度:
确定一个物体在空间位置所需要的独立坐标数目。
4.一个分子的平均动能为:
k2kT
2.气体分子的自由度
单原子分子(如氦、氖分子)i3;刚性双原子分子i5;刚性多原子分子i6
3.能均分原理:
在温度为T的平衡状态下,气体分子每一自由度上具有的平均动都相等,其值为1kT
2
五.理想气体的内能(所有分子热运动动能之和)
1.1mol理想气体E-RT
2
3.一定量理想气体E-RT(m)
2M
第八章热力学基础主要内容
1.准静态过程(平衡过程)
系统从一个平衡态到另一个平衡态,过程。
2.热力学第一定律
中间经历的每一状态都可以近似看成平衡态
QEW;dQdEdW
1.气体WPdv
2.Q,E,W符号规定
国2
m
3.dEMCV^T
「m—、
或E2E1CVgmCT2T1)
M
CVgm
3.热力学第一定律在理想气体的等值过程和绝热过程中的应用
1.等体过程
W0
QEcvgm(T2T1)
2.等压过程
Wp(V2V1)R(T2T1)
QEWCpgm(T2T1)
CpgmCvgmR字R,热容比=1
2CVgm
3.等温过程
E2E10
mV2mP2
QtWtRTln」RTln-
MV1Mp1
4.绝热过程
Q0
WECvgm(T2T1)
绝热方程PVC1,V-1TC2,PTC3。
4.循环过程
特点:
系统经历一个循环后,E0
系统经历一个循环后Q(代数和)W(代数和)
1.正循环(顺时针)-----热机逆循环(逆时针)-----致冷机
2.热机效率:
WQQ21鱼
Q1Q1Q1
式中:
Q1------在一个循环中,系统从高温热源吸收的热量和;
Q2------在一个循环中,系统向低温热源放出的热量和;
3.卡诺热机效率:
□
T1
W=Q1-Q2——在一个循环中,系统对外做的功(代数和)
式中:
T1——高温热源温度;T2——低温热源温度;
4.
制冷机的制冷系数:
卡诺制冷机的制冷系数:
五•热力学第二定律
1.开尔文表述:
从单一热源吸取热量使它完全变为有用功的循环过程是不存在
的(热机效率为100是不可能的)。
2.克劳修斯表述:
热量不能自动地从低温物体传到高温物体
两种表述是等价的