菱形的性质与判定提高练习含答案.docx
《菱形的性质与判定提高练习含答案.docx》由会员分享,可在线阅读,更多相关《菱形的性质与判定提高练习含答案.docx(11页珍藏版)》请在冰豆网上搜索。
菱形的性质与判定提高练习含答案
菱形的性质与判定提高练习
、选择题:
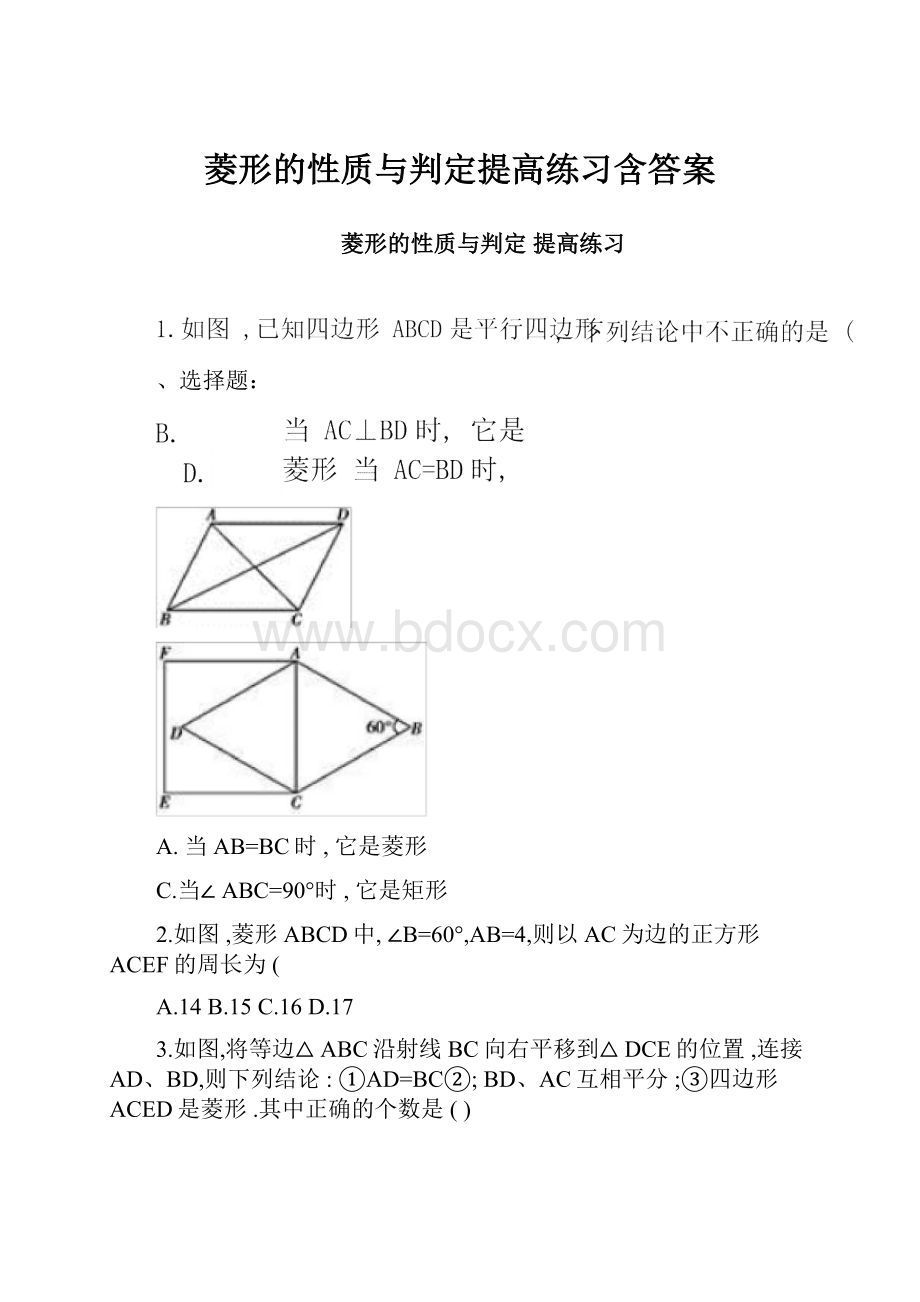
A.当AB=BC时,它是菱形
C.当∠ABC=90°时,它是矩形
2.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为(
A.14B.15C.16D.17
3.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC②;BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是()
A.0B.1C.2D.3
4.下列命题中错误的是()
A.平行四边形的对角线互相平分B.菱形的对角线互相垂直
C.同旁内角互补D.矩形的对角线相等
5..如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为()
A.22B.422C.6D.82
6.菱形的两条对角线长分别是6和8,则此菱形的边长是()
A.10B.8C.6D.5
7.如图所示,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()
或60°D.30°或60°
8.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状()
9.
A.仅仅只是平行四边形
9.已知?
ABCD,给出下列条件?
ABCD成为菱形的条件是(
B.是矩形C.是菱形D.无法判断
:
①AC=BD②;∠BAD=90°;③AB=BC;④AC⊥BD,添加其中之一能使)
A.①③B.②③C.③④D.①②③
10.如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为
A.4B.2.4C.4.8D.5
11.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),四边形ABCD是()
A.矩形B.菱形C.正方形D.梯形
12.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是()
A.163B.16C.83D.8二、填空题:
13.如图,已知矩形ABCD中,AB=8cm,AD=10cm,E、F、G、H分别是AB、BC、CD、DA的中点,
2
则四边形EFGH的面积等于cm2.
14.如图,在菱形ABCD中,AC=6,BD=8,则这个菱形的边长为
15.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是(写出一个即可).
16.如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于cm.
17.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为.
18.如图所示,在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm.那么,菱形ABCD的面积是,对角线BD的长是.
19.在图中所示的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个小
正方形的边长均为1,则该菱形的面积为.
20.如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点.若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为.
三、解答题:
21.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:
四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则当BE=时,四边形BFCE是菱形.
22.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:
四边形ADCF是菱形.
23.如图,已知在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:
△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
24.
(1)如图,纸片?
ABCD中,AD=5,S?
ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为()
A.平行四边形B.菱形C.矩形D.正方形
(2)如图,在
(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D.
①求证:
四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长
图1
图2
25.已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有AF=DE,AF⊥DE成立.
试探究下列问题:
(1)如图17①,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论是否仍然成立?
(请直接回答“成立”或“不成立”,不需要证明)
(2)如图17②,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论是否仍然成立?
若成立,请写出证明过程,若不成立,请说明理由;
(3)如图17③,在
(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
参考答案
1.答案为:
D;
2.答案为:
C;
3.答案为:
D;
4.答案为:
C;
5.答案为:
A;
6.答案为:
D;
7.答案为:
D;
解析:
画出所剪的图形示意图如图
8.答案为:
C;
9.答案为:
C;
10.答案为:
C;
11.答案为:
B;
12.答案为:
C;
13.答案为:
40
14.答案为:
5;
15.答案为:
C;B=BF或BE⊥CF或∠EBF=60°或BD=BF(答案不唯一)
16.答案为:
16.
17.答案为:
24;
18.答案为:
83cm;43cm;
19.答案为:
12;
20.答案为:
23-2
解析:
当等腰△PBC以∠PBC为顶角时,点P在以B为圆心,BC为半径的圆弧AC上.连接AC、BD相交于点O.若使PD最短,则点P在如图所示的位置处.
11
∵四边形ABCD是菱形,∴AC⊥BD,∠ABO=∠ABC=30°,∴AO=AB=1,∴BO=3,∴BD=2BO=23,∵PB=BC=2,∴PD=BD-PB=23-2.
当等腰△PBC以∠PCB为顶角时,易知点P与点D重合(不合题意,舍去)或点P与点A重合,则PD=2.
当等腰△PBC以BC为底边时,如图,作BC的垂直平分线交BC于点E,易知该直线过点A,则点P在线段AE上(不含点E).当P与A重合时,PD最短,此时PD=2.
∵2-2<2,∴PD的最小值是2-2.
21.
(1)证明:
∵AB=DC∴,AB+BC=DC+BC∴,AC=DB.
在△AEC和△DFB中,AC=DB,∠A=∠D,AE=DF∴△AEC≌△DFB(SAS),∴EC=BF,∠ACE=∠DBF.∴EC∥BF,∴四边形BFCE是平行四边形.
(2)4.当四边形BFCE是菱形时,BE=CE,∵AD=10,AB=CD=3,∴BC=10-3-3=4,∵∠EBD=60°,∴BE=BC=4,∴当BE=4时,四边形BFCE是菱形.
22.证明:
∵AF∥BC,∴∠EAF=∠ECD,∠EFA=∠EDC,又∵E是AC的中点,∴AE=CE,∴△AEF≌△CED.∴AF=CD,又AF∥CD,∴四边形ADCF是平行四边形.
∵AC=2AB,E为AC的中点,∴AE=AB,由已知得∠EAD=∠BAD,又AD=AD,∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.∴四边形ADCF是菱形.
23.解:
(1)证明:
∵四边形ABCD是矩形,∴AB=DC∠,A=∠D=90°.∵M为AD的中点,∴AM=DM.
在△ABM和△DCM中,AM=DM,∠A=∠D,AB=CD∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
∵N、E、F分别是BC、BM、CM的中点,11
∴NE∥CM,NE=CM,MF=CM,∴NE=FM∴,四边形MENF是平行四边形22
∵△ABM≌△DCM∴,BM=CM.
11
∵E、F分别是BM、CM的中点,∴ME=BM,MF=MC,∴ME=MF,22
∴平行四边形MENF是菱形.
(3)2:
1.
24.解:
(1)C.
(2)①证明:
∵AD=BC=5,S?
ABCD=15,AE⊥BC,∴AE=3.如图,∵EF=4,∴在Rt△AEF中,AF=5.∴AF=AD=5.又△AEF经平移得到△DE'F',∴AF∥DF',AF=DF',∴四边形AFF'D是平行四边形.又AF=AD,∴四边形AFF'D是菱形.
②如图,连接AF',DF.
在Rt△DE'F中,∵E'F=E'E-EF=5-4=1,DE'=3,∴DF=10.
在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,∴AF'=310.
∴四边形AFF'D的两条对角线长分别为10,310.
25解:
(1)成立.
(2)成立.理由:
∵四边形ABCD为正方形,∴AD=DC∠,BCD=∠ADC=90°.在△ADF和△DCE中,DF=CE,∠ADC=∠BCD,AD=C∴D△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE.
∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE.(3)四边形MNPQ是正方形.
理由:
如图,设MQ交AF于点O,PQ交DE于点H,∵点M,N,P,Q分别为AE,EF,FD,AD的中点,
11∴MQ=PN=DE,PQ=MN=AF,MQ∥DE∥PN,PQ∥AF∥MN,
22∴四边形GHQO是平行四边形,∵AF=DE,∴MQ=PQ=PN=M∴N,四边形MNPQ是菱形.∵AF⊥DE,∴∠AGD=90°,∴∠HQO∠=AOQ∠=AGD=90°,∴四边形MNPQ是正方形.