理力答案第六章.docx
《理力答案第六章.docx》由会员分享,可在线阅读,更多相关《理力答案第六章.docx(41页珍藏版)》请在冰豆网上搜索。
理力答案第六章
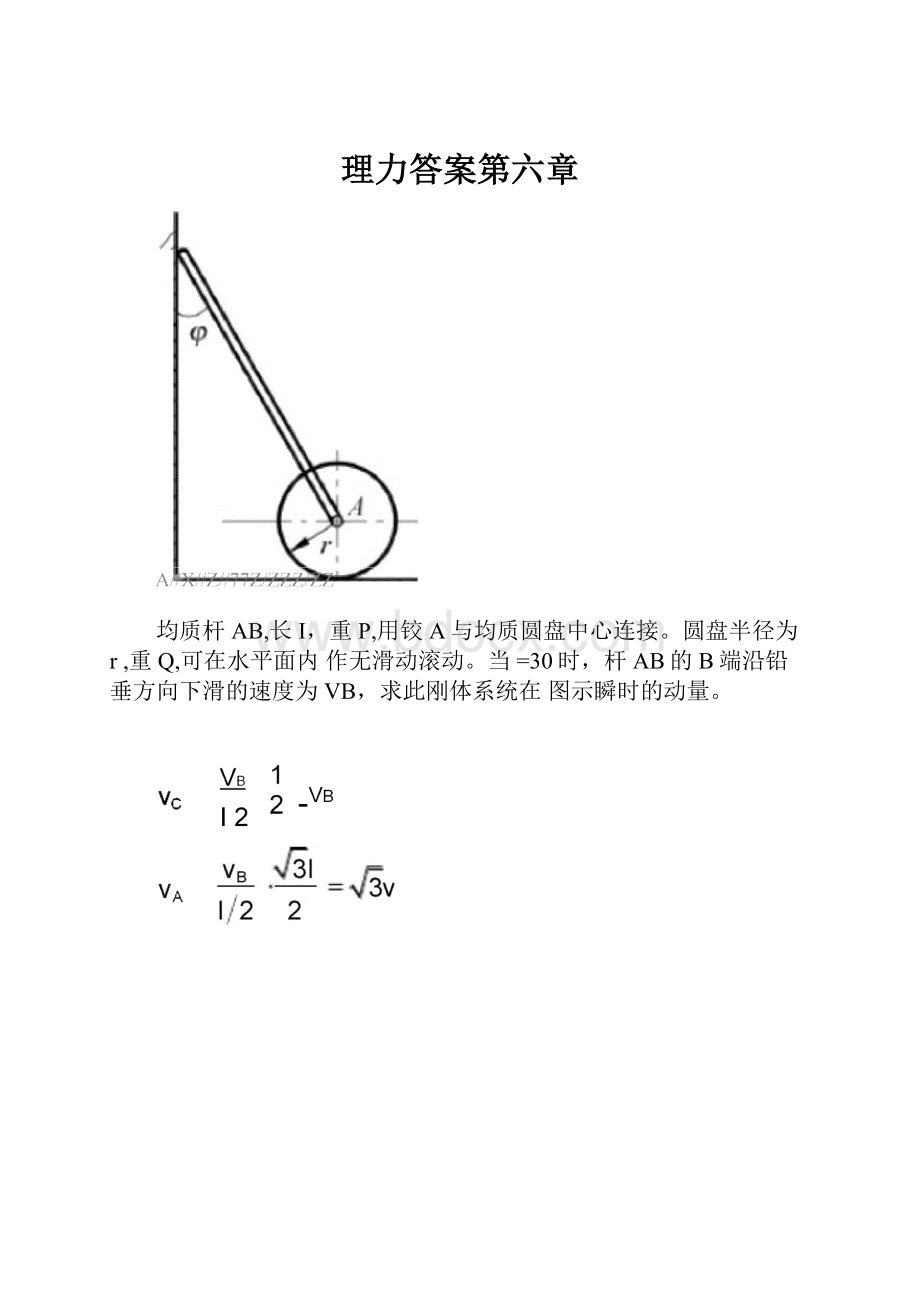
均质杆AB,长I,重P,用铰A与均质圆盘中心连接。
圆盘半径为r,重Q,可在水平面内作无滑动滚动。
当=30时,杆AB的B端沿铅垂方向下滑的速度为VB,求此刚体系统在图示瞬时的动量。
解:
AB杆的瞬心D如图所示,故其质心C的速度为
Vb
2g
往复式水泵的固定外壳部分D和基础E的质量为mi,均质曲柄0A长为r,质量为m2。
导杆B和活塞C作往复运动,其质量为m3。
曲柄0A以匀角速度,绕0轴转动。
求水泵基础
给地面的压力。
D和基
解:
建立坐标系,x轴水平向右为正方向,y轴竖直向上为正方向。
系统中外壳础E固定,曲柄0A作匀速转动,并带动导杆和活塞平动。
系统的总动量为:
r
p=m2costisinj亠m3r■sin,tj
由y方向的动量定理得:
S'Fy
dt
r22
m2costm3r,cos二N-[milm2m3g2
12
N=m!
m2m3gm22m3r■cost
2
图示凸轮机构中,凸轮半径为r、偏心距为e。
凸轮绕A轴以匀角速•’转动,带动滑杆D在套筒E中沿水平方向作往复运动。
已知凸轮质量为m1,滑杆质量为m2。
试求在任意瞬时机
座螺栓所受的动反力。
解:
取凸轮、滑杆
和机座组成的系
统为研究对象。
由于只
求动反力,故不
考虑重力,受力图如图
示。
凸轮质心的加速
度为:
aC1x--e■2cost
aciy=-e■2sint
滑杆质心的加速度为:
aC2x--e-2costaC2y=0
由质系动量定理得:
-me2cost-m2e2cost=F
2
-m1esint=N
所以:
2
F--(mhm2)e■cost
N=-mi|e2sint
图示小球P沿大半圆柱体表面由顶点滑下,小球质量为m2,大半圆柱体质量为m,半径为
R,放在光滑水平面上。
初始时系统静止,求小球未脱离大半圆柱体时相对图示静止坐标系的运动轨迹。
解:
根据题意,视小球为质点,大半圆柱体作平动。
系统在水平方向动量守恒。
设小球水平方向的位移为x,竖直方向的位移为y,则大半圆柱体质心在水平方向的位移为
(m2/mi)x,由图示几何关系,有,
222
(x(m2/mi)x)yR
化简为,
miR
即小球运动轨迹为一椭圆。
图示系统中,物块A的质量为m,小车B的质量为M,弹簧刚度系数为k,斜面光滑。
不计轮子的质量,试建立系统的运动微分方程。
解:
取系统为研究对象。
系统具有两个自由度,取x和s为广义坐标,其中s的原点取
在物块A的静平衡位置处。
系统在水平方向不受力,故由动量定理在x方向的投影式得:
m(XScos:
•)MX=0
再取物块A为研究对象,列写牛顿第二定律在s方向的投影式,得:
m(SXcos:
)=mgsin—ks
\k
将两式整理后得:
(mM)Xmgcos:
=0
msmXcosx,ks=0
两质量都等于M的小车,停在光滑的水平直铁轨上。
一质量为m的人,自一车跳到另一车,并立刻自第二车跳回第一车。
证明两车最后速度大小之比为M:
(M+m)。
解:
根据题意,这系统(人和两小车)在水平方向上动量守恒。
设最终状态两车的速度
大小分别为⑷和口v2,则由动量守恒定理知
Mvj-(Mm)v2=0
于是,两车最后的速度大小之比为
v2:
M=M:
(Mm)
如图所示,质量为m的偏心轮在水平面上作平面运动。
轮子轴心为A,质心为C,AC=e;
轮子半径为R,对轴心A的转动惯量为JA;C、A、B三点在同一铅直线上。
(1).当轮子只滚不滑时,若VA已知,求轮子的动量和对地面上B点的动量矩。
(2).当轮子又滚又滑时,若VA和已知,求轮子的动量和对地面上B点的动量矩。
解:
(1)轮子只滚不滑时轮子的动量为:
R+e
p=mv:
二RRemvA
对地面上B点的动量矩,利用Lb二LCrBCP,投影后为:
L^Lcm(Re)2;R
:
Ja=Jcme2
Lc=(Ja-me2)*
故有:
Lb二[Ja-me2m(Re)2]巻R
(2)轮子又滚又滑时轮子的动量为:
p二mvc二m(VAe)
对地面上b点的动量矩:
Lb二Lcm(Re)(VAe)
Lc=(Ja-me2)•
Lb=(JameRr、亠(Re)mvA
水平圆盘可绕铅垂轴z转动,如图所示。
其对z轴的转动惯量为Jz。
一质量为m的质点,
在圆盘上作匀速圆周运动,圆周半径为r,速度为v0,圆心到盘心的距离为I。
开始运动时,
质点在位置A,圆盘角速度为零。
试求圆盘角速度■与角「间的关系。
轴承摩擦略去不计。
V
■r
系统在初始时刻对z轴的动量矩为:
L°i=m(lr)Vo
系统在任意时刻对z轴的动量矩为:
Lo2=Jz■[Pm(vevr)]k
其中:
Ve二亍■,Vr二V
:
:
二.l2r22lrcos
2
[pmve]k=m?
-■
[pmvr]k=mv0cos(Ircos)mv0sinrsin
二mv0(lcos「r)
由LO1=Lo2得:
2
m(l+r)v0=J乙㈢+mP国+mv0(lcos®+r)
mv0I(1-cos®)
Jzm(l2r22rlcos:
)
故有
Jo;^m1gl1/2
由质心运动定理
m|XC1m2xC2二X—;
miycim2yc2=丫-mp-m2g
Y=m^gm2ggyCim2yC2二(m^m2)g-mJi;/2-m2l2;-449.167N
2求杆EC在A处的弯矩
取杆OA为研究对象,将其惯性力系向O点简化,受力图如图示,其中惯性力S和惯性力偶
矩Ms分别为
l1/3
mug
2
S=口初;/2Mm1l1J3
对A点列写力矩平衡方程
l1
MAMSm1g-(YS)h=0
解得
Ma=(Y+S)I「Ms-
=272.225Nm
匀质滚子的质量为m,半径为R,放在粗糙的水平地板上,如图所示。
在滚子的鼓轮上绕以绳,在绳子上作用有常力T,作用线与水平方向夹角为:
•。
已知鼓轮的半径为r,滚子对轴
O的回转半径为匚,滚子由静止开始运动。
试求滚子轴O的运动方程。
解法一:
列写刚体平面运动微分方程
mXO二Tcos:
-F
0=Tsin:
-mgN
m-O--TrFR
补充运动学方程:
Xo=R;
联立求解,得:
□TR(Rcos。
—r)
=m(R2韦)
将上式积分两次,并考虑到滚子初始静止,得:
2
TR(Rcos。
-r)t
冷-m(R2弋)空
图示重物A的质量为m,当其下降时,借无重且不可伸长的绳使滚子C沿水平轨道纯滚动。
绳子跨过定滑轮D并绕在滑轮B上。
滑轮B与滚子C固结为一体。
已知滑轮B的半径为R,滚子C的半径为r,二者总质量为M,其对与图面垂直的轴0的回转半径为「。
求重物A的加速度。
解:
重物A作平动,滚子C作平面运动。
分别取重物A和滚子C为研究对象,列出其运动微分方程。
对重物A
ma二mg-T
对滚子C
mXo二T-F
MY;=Fr-TR
滚子只滚不滑
Xo二r;
取O为基点,分析E点的加速度
联立求解
mg(R-r)
222
Mr2:
mR-r
图示匀质圆盘的质量为16kg,半径为0.1m,与地面间的动滑动摩擦系数」二0.25。
若盘
心O的初速度vO=0.4m/s,初角速度-■=2rad/s,试问经过多少时间后球停止滑动?
此时盘心速度多大?
解:
圆盘作平面运动,运动微分方程为
mxo=_F
myo=0=N-mg
1mR2;=FR
2
由于圆盘又滚又滑,故有
F
Xo—g「,;=2g」/R
(1)求经过多少时间后盘停止滑动。
盘停止滑动的条件是
Xq=R-
由初始条件可得t时刻
Xq=Vq'Xqt,■~~'Q
.t=-(Rqvq)/(Xq-R;)=(Rqvq)/3g」=0.0816s
(2)求此时盘心的速度
Xq=Vq-g.Lt=0.2m/s
图示匀质细长杆AB,质量为m,长度为I,在铅垂位置由静止释放,借A端的小滑轮沿倾
角为二的轨道滑下。
不计摩擦和小滑轮的质量,试求刚释放时点A的加速度。
在光滑的水平面上平放着一半径为a、质量为M的圆环。
环上有一质量为m的甲虫,原来
静止,后甲虫沿圆环爬行,求甲虫和圆环中心的轨迹。
解:
设甲虫的运动速度为V1,圆环的运动速度为V2,系统质心速度为vq,由动量守恒
得:
mqMv2=(mM)Vo=0
所以系统质心速度为0。
以圆环中心为原点,圆环中心和甲虫的连线为x轴建立坐标系,由系统质心计算可得:
ma=(mM)x
ma
x=
m+M
若圆环圆心不动,则系统质心的轨迹随甲虫爬动为一半径为
ma
的圆。
现在系统质心不
mM
的圆。
mM
5:
..21o
为一圆,圆心在O,半径为卫do
m+M
问哪个球
均质的空心球壳和实心圆球,沿着同一斜面自同一高度同时无初速无滑动地下滚,滚得快一些?
证明:
它们经过相等距离所需的时间之比为
证明:
本问题中球体具有一个自由度,取x为广义坐标。
其受力图如题中所示。
由刚体平面运动微分方程得到:
rnijXj=mgsina-Fi
M-mgcos。
=o
JiXFiR
由纯滚动,补充运动学方程:
对i=1或2,方程
(1)—(4)中分别为球壳和圆球的运动方程。
联立四个方程得到:
gsin:
mJi
2
j+mR
^gsin:
对于球壳和圆球有:
J2=—m2R
5
从而,
2
1
X1
J1gR;
1境
21
X2■
2'
m2R2
_1'
-25
J2m2R;
1艺
即实心圆球比空心球壳下降得快。
由于球沿斜面的加速度为常数,初始速度为零,因此
12
xxt。
经过相等的距离所需时间之比为:
2
&_-.J?
__5_
t2顶、、歹
即证。
球1速度Vi=6m/s,方向与静止球2相切,如图所示。
两球半径相同、质量相等,不计摩
n和切线
解:
两球碰撞时位置如图所示,将两球碰撞前后的速度向两球接触面的公法线
t上投影,设碰撞后两球的速度为u和u2,则法向分量记为v1n,u1n,u2n,切向分量记为
由几何关系知v-30,故v1n=6cost-3.3m/s,v1=6sin-3m/s。
V
碰撞前后质系在法向上动量守恒,两小球各自在切向上动量守恒,因此两球碰撞的动力
学方程为:
由
(2)(3)可解出:
又根据恢复系数有:
(1)、(4)式联立解得:
mv^=mu^
U1=3m/s,U2=0
u1n=—V3m/s
5
u?
n—3m/s
5
即:
Ui=3.175m/s,氏=4.157m/s。
质量为0.2kg的球以水平方向的速度v=48km/h打在一质量为2.4kg的匀质木棒上,木棒
的一端用细绳悬挂于天花板上。
若恢复系数为0.5,试求碰撞后木棒两端A、B的速度。
解:
设碰撞后小球的速度为U1,木棒质心C点的速度为U2,其角速度为「。
取整体系统为研究对象,设球与杆的撞击点为D,绳的上方悬挂点为0。
系统对0点的动量矩守恒,且在水平方向动量守恒,即
m-ivOD=m1u1ODJCm2u2OC
m^=m1u1m2u2
补充运动学方程:
恢复系数的定义:
联立求解得:
,罟rad/s
U2=1.5m/s
从而木棒两端A、B的速度分别为:
uA=u2-AC•-0uB=u2CB=3m/s
匀质杆长为I,质量为m,在铅垂面内保持水平下降并与固定支点E碰撞。
碰撞前杆的质心
速度为vC,恢复系数为e。
试求碰撞后杆的质心速度uC与杆的角速度「。
解:
杆在碰撞前作平动,碰撞后作平面运动。
受力图如图示。
列写平面运动动力学方程,得:
muC-mvC=_S
-0=-S-
4
由恢复系数的定义,得:
联立求解得:
质量为mi的直杆A可以自由地在固定铅垂套管中移动,杆的下端搁在质量为m2,倾角为:
的光滑楔子B上,楔子放在光滑的水平面上,由于杆子的重量,楔子沿水平方向移动,杆下落,如图所示。
求两物体的加速度大小及地面约束力。
解:
系统为一自由,取整体系统为研究对象。
由运动学关系得
根据动量定理,对于A杆
联立
(1)和
(2)得
m^g
m2mi|sec2:
m2mi|tan2:
■
质量为30kg的小车B上有一质量为20kg的重物A,已知小车在120N的水平力P作用2s后
移过5m。
不计轨道阻力,试计算A在B上移过的距离。
解:
已知mA=20kg,mB=20kg,P=120N,t=2s,sB=5m。
由质点运动学公式有
aB=2爭=225=2.5m/s2t222
若将小车B和质量A看作一个系统,在水平方向,由质系动量定理
m^aA+m^aB=P
于是
aA=PFBaBJ20—30°5=2.25m/s2mA20
这样
1212
sA=—aAt=—x2.2^2=4.5m
22
则A在B上移过的距离
Sab=SB一SA=5一4.5=0.5m
如图所示,水平面上放一均质三棱柱A。
此三棱柱上又放一均质三棱柱B,两三棱柱的横截
面都是直角三角形,三棱柱A比三棱柱B重两倍。
设三棱柱和水平面都是绝对光滑的。
(1)
试列写系统运动微分方程
(3)求水平面作用于三棱柱A的反力。
解:
取水平向右为X轴正方向,系统具有两个自由度,取A的绝对位移X和B的相对位移xr为广义坐标。
设mB=m,则mA=3m,由水平方向动量守恒,得
・・・・・・・・・・
mBxcosh"xmAx=0,即4xxrcosa=0
(1)
对B沿斜面方向由动量定理得:
mBxrxcos:
=mBgsin:
,即xcosaxr-gsina=0
(2)
上两式即为系统运动微分方程。
当B沿A下滑至水平面时,绝对位移冰A二-s,.ixB=a-b-s
由mAXamB%=0
1
得三棱柱A的位移s(a-b)。
4
在竖直方向由动量定理:
N-mAg「mBg=-mBXrsin〉
即n=12mg
4-cos2a
如图所示均质圆盘,半径为R,质量为m,不计质量的细杆长丨,绕轴o转动,角速度,,求下列三种情况下圆盘对固定轴O的动量矩。
(1)圆盘固结于杆;
(2)圆盘绕A轴转动,相对于杆的角速度为;
(3)圆盘绕A轴转动,相对于杆的角速度为■o
解:
(1)圆盘固结于杆:
Lo-LA'rOAP
一12
圆盘对质心A的动量矩为:
一mR2国
2
质心A对固定轴O的动量矩为:
ml2-
所以圆盘对固定轴O的动量矩为:
(丄mR2ml2)■
2
(2)圆盘绕A轴转动,相对于杆的角速度为—:
圆盘平动,圆盘对固定轴O的动量矩为:
ml2.
(3)圆盘绕A轴转动,相对于杆的角速度为-■:
同
(1)可得圆盘对固定轴O的动量矩为:
(丄mR2+ml2)们+2mR2们=ml2⑷+mR2o
22
B点,杆开始保持如图所示垂
均质杆AC质量为30kg,有一水平力240N突然作用于杆上直位置。
(1)若不考虑水平表面与杆之间的摩擦力,试决定此瞬时杆端C的加速度;
(2)若AC杆与水平表面之摩擦系数为0.30,试求C点的初加速度。
解:
根据题意
(1)无水平摩擦力的情况
240=ma°x
N—mg=ma°y
12
240ml2;
12
:
=6rad/s2
acxiacyj=aoxiaoyj—(l/2)二'i
联立以上各式,解得
S二-4m/s2
(2)考虑水平方向有摩擦力的情况
240-mg0.3二maox
240—0.6mg=gml2;
联立解得
2
比乂=1.88m/s
半径为r的均质圆盘在铅垂平面内绕水平轴A摆动(如图示)。
设圆盘中心O至A的距离为
b,问b为何值时,摆动的周期为最小?
求此最小周期。
解:
圆盘绕A点的转动惯量为
2122
J=JOmbmrmb
2
根据动量矩定理,可以得到
J,mgbsin二-0
因为是小转角,所以sinv,所以
1
(mrmb)亠mgb〒-0
小值,
一圆环由绳AB和光滑斜面支承。
圆环质量为10kg、半径为2m,质量为3kg的质点D与
圆环固结如图所示。
求当绳子剪断的瞬时质点D的加速度。
解:
如图,建立平动参考系Oxy。
绳AB剪断的瞬时,圆环的受力如图所示。
此瞬时圆环的角速度为零,角加速度为;,圆环中心C的速度为零,加速度为aO。
D点速度为零,加速度aD为:
(1)
ad=ae-a「=a。
;Rt
其中T沿圆环切线方向。
圆环和质点组成的系统对圆环中心O点的动量矩为:
2
L。
一mR•‘kEdm2Vd
其中,
从而,
L。
=—gRbk+r°D汉m,(Vo+®Rt)=一m|R2⑷k-mtR2⑷k-m2RvOcosl5k
由公式:
在初始时刻vO=0,有:
(5)(6)代入
(1)得到D的加速度aD为:
.(m+叫)2cos30‘-m;sin45m2gsin45-m2aOcos15
ad=a。
i-Rt22giRt
(m+mD-m|cosi5(m+m2)R
=0.8733gi-0.0315g^0.8429gi-0.0082gj
^0.4144g|1-0.734®=4.06^-7.19j1
解:
杆作平面运动,受力图如下所示,取二为广义坐标。
先假
设B端不滑动,在该瞬时杆绕B点作定轴转动,则质心C坐标为
1.1.
xClcos:
yClsin二
22
质心加速度为
yc^sin"2IcosZ
22
Xc二_fcos"'2-〔sind
由刚体平面运动微分方程得
1_2■■■
_m(cos=sin二v)=F
2
1'2
m-(-sin门cosn)=N-G
2
12…l
ml-Gcosv
32
代入v-30-0到上式,得
73、3
N=G,F二G
1616
其中F/N=3、、3/7.0.3,可知B端必然滑动。
在任意时刻,质心C的y方向坐标满足
yC=-】sin"2-cos丁口
22
由刚体平面运动微分方程得
12
m—(—sinrcos门)=N-G
2
代入当前瞬时v-30-0,到上式,得
m~1N(f-一3)
124
解得
N=35N,F=10.5N,也=-14.7rad/s2(顺时针方向)
如图所示,一球放在水平面上,其半径为r。
在球上作用一水平冲量S,求当接触点A无滑动时,冲量距水平面的高度h应为多少?
不考虑摩擦力的冲量。
解:
对质心分别运用动量定理和动量矩定理
S=mvc
S(h-r)=J•
22
其中球体的转动惯量为Jmr2
5
由于球体没有滑动,所以
vC=r
22Vc
j‘5mr~77
hr二5rr
SmVd5
三根杆开始为静止,AB=BD=2CD二丨,彼此用铰链连接,AB、CD铅垂,BD水平。
AB、
BD质量为m,CD质量为1m,在AB杆上有一水平冲量S作用,求AB杆的角速度。
假设
铰链都是光滑的。
Sbb
B%
注意到BD杆瞬时平动且速度为:
BD=用1,CD角速度为「CD=2.,由动量矩定理的有限形
式有:
12
Sh-Sgl二Jabrnl■■-
3
S^_SD-mVB^-ml'
。
I1“ml2①
SDJDC'CD-
212
于是
2Sh
3ml2
两球的质量各为m、m2,分别用长为ii、I2的两根不可伸长的绳子平行地挂起,使两球的
中心在同一水平上并且紧挨着。
今使m-j球与竖直线偏离角,然后无初速地释放,若恢复
系数为e,求第二个球的最大偏角:
-°
解:
对球1,设碰撞前的速度为v1,则:
12
ggh1-cosm1v1
2
2g|1吒
设碰撞后球1的速度为u1,球2的速度为U2。
由水平方向动量守恒:
my二m)u1m2u2
由恢复系数:
求得
garcsiJmUjTsinT
jm^m2Yl22
n角,自高处无初速地落下时与光滑水平面作完全非弹性碰
一长为2a的均匀杆与竖直线成撞。
证明:
若杆中心下落高度
22
Ha(13sinRH
18sin日cos日
则杆的下端与地面接触后又立刻离开地面。
证明:
设碰撞前瞬间杆子速度为Uo,碰撞后瞬间杆子质心C速度为Ucx,UCy,转动角速度
为•1。
碰撞后的动力学方程为
muc^Ie=0
m(u°-Ucy)=I
ee-i
Jc(1-0)=Jc1=Mc(l)=lyasin^
杆与地面发生完全非弹性碰撞,故碰撞后瞬间
UAy=0,即只有水平方向速度,而质心只有
Ucy
竖直方向的速度,杆转动瞬心为图示点E,可知-一—,代入运动方程得
asin0
JeC^=^ma2—Cy—=Iyasin日=m(u0—uCy)asin日
3asinG
2
3u0sinr
UCy
2
3sin「1
3sins•、顽(方向竖直向下)
3sin二T