极限的概念.ppt

极限的概念.ppt

《极限的概念.ppt》由会员分享，可在线阅读，更多相关《极限的概念.ppt（37页珍藏版）》请在冰豆网上搜索。

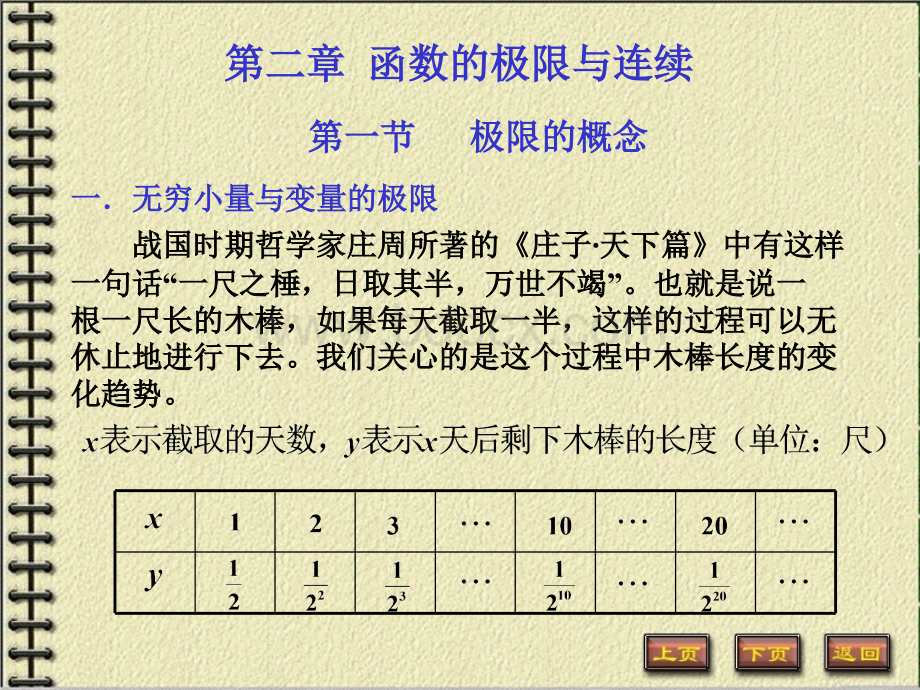
第二章第二章函数的极限与连续函数的极限与连续战国时期哲学家庄周所著的战国时期哲学家庄周所著的庄子庄子天下篇天下篇中有这样中有这样一句话一句话“一尺之棰，日取其半，万世不竭一尺之棰，日取其半，万世不竭”。

也就是说一。

也就是说一根一尺长的木棒，如果每天截取一半，这样的过程可以无根一尺长的木棒，如果每天截取一半，这样的过程可以无休止地进行下去。

我们关心的是这个过程中木棒长度的变休止地进行下去。

我们关心的是这个过程中木棒长度的变化趋势。

化趋势。

一一无穷小量与变量的极限无穷小量与变量的极限第一节第一节极限的概念极限的概念从表中可以看到，当截取的天数越来越多时，剩余木从表中可以看到，当截取的天数越来越多时，剩余木棒的长度越来越小，并且随着天数的无限增大，剩余长度棒的长度越来越小，并且随着天数的无限增大，剩余长度可以无限的减小，其绝对值可以小于任意给定的正数。

可以无限的减小，其绝对值可以小于任意给定的正数。

如要如要只需只需，即截取，即截取1010天天如要如要只需只需，即截取，即截取2020天天如果某个变量如果某个变量的变化趋势是：

其绝对值的变化趋势是：

其绝对值越来越越来越小，可以小于任意事先给定的正数，则称此变量小，可以小于任意事先给定的正数，则称此变量无限趋无限趋近于近于00，记为，记为。

如果某个变量如果某个变量的变化趋势是：

其绝对值的变化趋势是：

其绝对值越来越越来越大，可以大于任意事先给定的正数，则称此变量大，可以大于任意事先给定的正数，则称此变量趋近于趋近于无穷大，记为无穷大，记为。

定义：

定义：

设设是一个变量，是一个变量，是一个常数是一个常数

（1）

（1）如果如果无限趋于无限趋于00，则称，则称的极限为的极限为00，并称，并称为无穷为无穷小量，记为小量，记为；

（2）

（2）如果如果无限趋于无限趋于00，则称，则称的极限为的极限为，记为，记为；（3）（3）如果如果趋于趋于，则称，则称的极限不存在，并称的极限不存在，并称为无穷为无穷大量，记为大量，记为。

表示变量表示变量无限趋于无限趋于00表示变量表示变量无限趋于常数无限趋于常数表示变量表示变量沿着沿着轴正向趋于轴正向趋于表示变量表示变量沿着沿着轴负向趋于轴负向趋于当当是是的函数时，的函数时，的变化趋势由的变化趋势由的变化趋势决定的变化趋势决定例例11：

判断下列函数当判断下列函数当和和时，是否为无穷小量？

时，是否为无穷小量？

（1）

（2）（3）（4）解：

解：

由函数图形可知由函数图形可知为无穷小量为无穷小量为无穷大量为无穷大量由函数图形可知由函数图形可知为无穷小量为无穷小量为无穷大量为无穷大量由函数图形可知由函数图形可知由函数图形可知由函数图形可知为无穷大量为无穷大量为无穷小量为无穷小量为无穷小量为无穷小量为无穷大量为无穷大量例例22：

指出当指出当趋于何值时，趋于何值时，是无穷小量？

是无穷小量？

（1）

（2）（3）为无穷小量为无穷小量为无穷小量为无穷小量为无穷小量为无穷小量说明：

说明：

（1）自变量不同的变化趋向得出因变量的变化趋向是不一自变量不同的变化趋向得出因变量的变化趋向是不一样样的。

的。

（2）看函数的变化趋势主要是从函数的图像上去看，所以要看函数的变化趋势主要是从函数的图像上去看，所以要熟悉函数的图像。

熟悉函数的图像。

“割之弥细，所失弥割之弥细，所失弥少，割之又割，以少，割之又割，以至于不可割，则与至于不可割，则与圆周合体而无所失圆周合体而无所失矣矣”11、割圆术：

、割圆术：

播放播放刘徽刘徽二、二、时，函数时，函数的极限的极限正十二边形的面积正十二边形的面积正正形的面积形的面积所失面积所失面积所失面积所失面积所失面积所失面积正六边形的面积正六边形的面积定义：

定义：

如果当如果当时，函数时，函数与常数与常数的差的差为无穷小量，即为无穷小量，即，则称，则称时，函数时，函数以常数以常数为极限，记为：

为极限，记为：

类似可定义当类似可定义当时以及时以及时，函数时，函数的极限的极限一般地一般地例例3：

求下列极限（求下列极限（常用要记住的！

常用要记住的！

）解：

解：

例例4：

求下列极限（求下列极限（常用要记住的！

常用要记住的！

）解：

解：

极限不存在或者无穷大量极限不存在或者无穷大量三、三、时，函数时，函数的极限的极限定义：

定义：

如果当如果当时，函数时，函数与常数与常数的差的差为无穷小量，即为无穷小量，即，则称，则称时，函数时，函数以常数以常数为极限，记为：

为极限，记为：

例例5：

求下列极限求下列极限以上几个都是有定义且有极限的情况以上几个都是有定义且有极限的情况此例是无定义而有极限的情况此例是无定义而有极限的情况-0.4-0.20.20.4-1-0.50.51（6）（6）如果如果，求求不存在不存在此例是有定义而无极限的情况此例是有定义而无极限的情况第二节第二节极限的运算法则极限的运算法则一一极限的四则运算法则极限的四则运算法则定理定理推论推论11常数因子可以提到极限记号外面常数因子可以提到极限记号外面.推论推论22该法则成立的前提是：

该法则成立的前提是：

都存在都存在例例1:

1:

求下列极限求下列极限解解:

定理：

初等函数在其定理：

初等函数在其定义区间内任一点的定义区间内任一点的极限值等于函数值。

极限值等于函数值。

二、计算有理分式极限的运算法则二、计算有理分式极限的运算法则（11）计算有理分式在）计算有理分式在极限的运算极限的运算例例22：

求下列极限求下列极限解解:

因为分母的极限为因为分母的极限为00，而分子极限为，而分子极限为88所以极限的四则运算法则不能用所以极限的四则运算法则不能用从而可以总结出下列从而可以总结出下列规律：

规律：

当当时，时，（代入即可）（代入即可）当当时，时，当当时，时，约去零因子约去零因子后的有理分式的极限（分子分母都要分解因式）后的有理分式的极限（分子分母都要分解因式）例例33：

利用上面的规律求下列极限利用上面的规律求下列极限解解:

分子分母分解因式分子分母分解因式（22）计算有理分式在）计算有理分式在极限的运算极限的运算例例44：

求下列极限求下列极限解解:

由于当由于当时，分子分母均趋于无穷大，极限不存在时，分子分母均趋于无穷大，极限不存在所以极限的四则运算法则不能用所以极限的四则运算法则不能用在分子分母中同时除以在分子分母中同时除以的最高次幂，可化为极限存在的情况的最高次幂，可化为极限存在的情况从而可以总结出下列从而可以总结出下列规律：

规律：

例例5：

利用以上规律求下列极限利用以上规律求下列极限解解:

三、无穷小量的运算法则三、无穷小量的运算法则

（1）非零无穷小量的倒数是无穷大量，反之亦然。

非零无穷小量的倒数是无穷大量，反之亦然。

（2）无穷小量与有界变量的乘积还是无穷小量。

无穷小量与有界变量的乘积还是无穷小量。

（3）有限个无穷小量之和还是无穷小量。

有限个无穷小量之和还是无穷小量。

例例6：

求下列极限求下列极限解解:

例例7:

求下列极限求下列极限解解: