数据库范式与关系模式示例Word格式文档下载.docx
《数据库范式与关系模式示例Word格式文档下载.docx》由会员分享,可在线阅读,更多相关《数据库范式与关系模式示例Word格式文档下载.docx(33页珍藏版)》请在冰豆网上搜索。
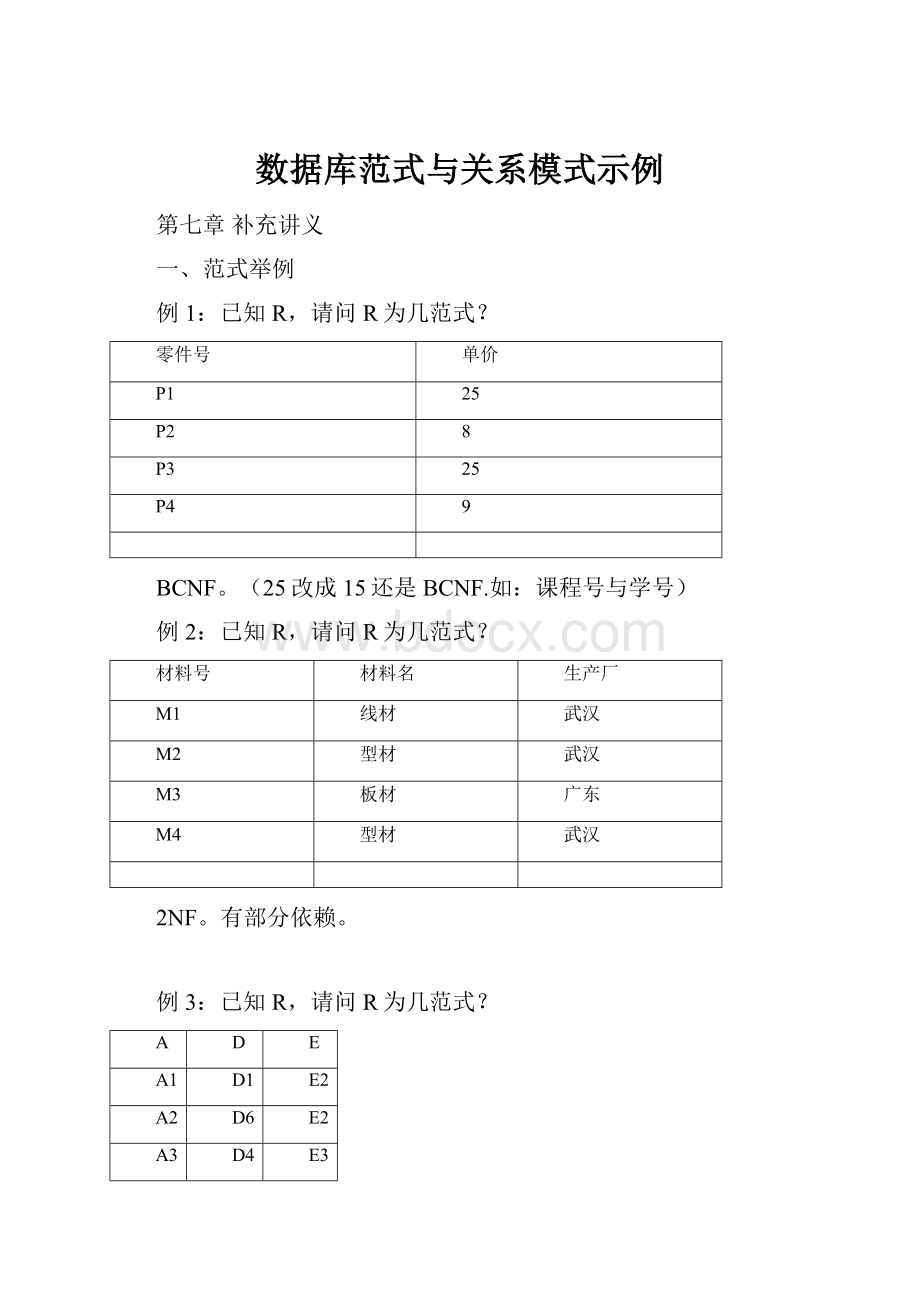
E3
A4
E4
例4:
R(X,Y,Z),F={XY->
Z},R为几范式?
BCNF。
例5:
R(X,Y,Z),F={Y->
Z,XZ->
Y},R为几范式?
3NF。
R的候选码为{XZ,XY},(R中所有属性都是主属性,无传递依赖)
二、求闭包
数据库设计人员在对实际应用问题调查中,得到的结论往往是零散的、不规范的(直观问题好办,复杂问题难办了),所以,这对分析数据模型,达到规范化设计要求,还有差距,为此,从规范数据依赖集合的角度入手,找到正确分析数据模型的方法,以确定关系模式的规范化程度。
例1.已知关系模式R(U、F),其中,U={A,B,C,D,E};
F={ABC,BD,ECB,ACB},求(AB)+F.
解:
设X(0)=AB
计算X
(1),在F中找出左边为AB子集的FD,其结果是:
ABC,BD
∴X
(1)=X(0)UB=ABUCD=ABCD显然,X
(1)≠X(0)
计算X
(2),在F中找出左边为ABCD子集的FD,其结果是:
CE,ACB
∴X
(2)=X
(1)UB=ABCDUBE=ABCDE显然,X
(2)=U
所以,(AB)+F=ABCDE.(等于U,所以AB是唯一候选关键字)
例2.设有关系模式R(U、F),其中U={A,B,C,D,E,I};
F={AD,ABE,BE,CDI,EC},计算(AE)+
令X={AE},X(0)=AE
在F中找出左边是AE子集的FD,其结果是:
AD,EC
∴X
(1)=X(0)UB=X(0)UDC=ACDE显然,X
(1)≠X(0)
在F中找出左边是ACDE子集的FD,其结果是:
CDI
∴X
(2)=X
(1)UI=ACDEI
显然,X
(2)≠X
(1),但F中未用过的函数依赖的左边属性已含有X
(2)的子集,所以不必再计算下去,即(AE)+=ACDEI.
因为,X(3)=X
(2),所以,算法结束。
三、求最小依赖集
最小依赖集是对函数依赖集合进行规范的结果,这样才能对一般关系模式进行准确分析。
例1.设函数依赖集F={ABCE,AC,GPB,EPA,CDEP,HBP,DHG,ABCPG},求与F等价的最小函数依赖集。
解:
将F中依赖右部属性单一化:
F1=ABCABE
HBPAC
DHGPB
DGEPA
ABCPCDEP
ABCG
由于有AC,所以ABC为多余成份:
所以F2=ABEHBP
ACDH
GPBDG
EPAABCP
CDEPABCG
经过分析认为F2中无多余依赖,则:
Fmin=F2为最小函数依赖集。
即Fmin={ABE,HBP,AC,DH,GPB,DG,EPA,ABCP,CDEP,ABCG}.
例2.已知F={AB,BA,BC,AC,CA},求Fmin.
解:
F1=ABAC
BABC
CA
Fmin1=ABAC
BACA
Fmin2=ABCA
BC
例3.已知F={AC,CA,BAC,DAC},求Fmin。
将F中依赖的右部属性单一化:
F1=ACCA
DADC
由于BA,AC,所以BC是多余成份。
又由于DA,AC,所以DC是多余成份。
所以F2=ACCA
BADA
因为F2中所有依赖的左部都是单属性,所以不存在依赖左部的有多余属性。
所以Fmin=ACCA
即Fmin={AC,CA,BA,DA}.
例4.设有关系模式R(U,F),其中:
U={E,F,G,H},F={EG,GE,FEG,HEG,FHE},求F的最小依赖集。
F1=EGHE
GEHG
FEFHE
FG
由于有FE,FHE为多余成份:
(不是因为有HE,而是,F后面加一个H和不加一样)
所以F2=EGHE
FEFG
由于F2中,FE和FG以及HE和HG之一为多余,则:
Fmin1={EG,GE,FG,HG}
Fmin2={EG,GE,FE,HE}Fmin3,Fmin4同理。
四、求候选码
1.候选关键字求解理论
对于给定的关系R(A1,A2,…,An)和函数依赖集F,可将其属性分为四类:
●L类:
仅出现在F的函数依赖左部的属性
●R类:
仅出现在F的函数依赖右部的属性
●N类:
在F的函数依赖左右两边均未出现的属性
●LR类:
在F的函数依赖左右两边均出现的属性
定理1:
对于给定的关系模式R及其函数依赖集F,若X(X∈R)是L类属性,则X必为R的任一候选关键字成员。
推论1:
对于给定的关系模式R及其函数依赖集F,若X(X∈R)是L类属性,且X包含了R的全部属性,则X必为R的唯一候选关键字。
定理2:
对于给定的关系模式R及其函数依赖集F,若X(X∈R)是R类属性,则X不在任何候选关键字中。
定理3:
设有关系模式R及其函数依赖集F,若X是R的N类属性,则X必包含在R的任一候选关键字中。
推论2:
对于给定的关系模式R及其函数依赖集F,若X是R的N类和L类组成的属性集,且X+包含了R的全部属性,则X必为R的唯一候选关键字。
2.单属性依赖集图论求解法(多属性不行)
I:
关系模式R,R的单属性函数依赖集F。
O:
R的所有候选关键字。
算法:
求F的最小依赖集Fmin。
构造FDG(函数依赖图)。
从图中找出关键属性集X(X可为空)。
查看G中有无独立回路,若无则输出X即为R的唯一候选关键字,转
,若有,则转
。
从各独立回路中各取一结点对应的属性与X组合成一候选关键字,并重复这一过程取尽所有可解的组合,即为R的全部候选关键字。
结束。
3.多属性依赖集候选关键字求解法
关系模式R及其函数依赖集F。
O:
将R的所有属性分为L,R,N和LR四类,并令X代表L,N两类,Y代表LR类。
求X+,若X包含了R的全部属性,则X即为R的唯一候选关键字,转
,否则,转
在Y中取一属性A,求(XA)+.若它包含了R的全部属性,则转
,否则,调换一属性反复进行这一过程,直到试完所有Y中的属性。
若已找出所有候选关键字,则转
,否则在Y中依次取2个,3个…,求它们的属性闭包,直到其闭包包含R的全部属性。
停止,输出结果。
例1.设R=(O,B,I,S,Q,D),F={SD,DS,IB,BI,BO,OB},求R的所有候选关键字。
Fmin={SD,DS,IB,BI,BO,OB}.
构造FDG.
关键属性集{Q}.(原始点和孤立点统称关键点。
)
有两个独立回路,SDS,IBOBI.
所以R的所有候选关键字为:
QSI,QSB,QSO,QDI,QDB,QDO.
例2.设R={X,Y,Z},F={XY,YX},求R的所有候选关键字。
Fmin={XY,YX}。
构造FDG
关键属性{Z}.
有1个独立回路,
1).候选关键字个数=各独立回路中结点个数乘积=2(1个回路,2个结点)。
2).候选关键字所含属性个数=关键属性个数+独立回路个数=1+1=2。
所以R的所有候选关键字为:
ZX,ZY.
例3.设有关系模式R(A,B,C,D),其函数依赖集F={DB,BD,ADB,ACD},求R的所有候选关键字。
经考虑F发现,A,C两属性是L类属性,由定理知,AC必是R的一候选关键字字成员。
又因(AC)+=ABCD,所以AC是R的唯一候选关键字。
例4.设有关系模式R(A,B,C,D,E,P),F={AD,ED,DB,BCD,DCA},求R的所有候选关键字。
经考察发现,C,E两属性是L类属性,故C,E必在R的任何候选关键字中,又P是N类属性,故P也必在R的任何候选关键字中。
又因(CEP)+=ABCDEP所以CEP是R的唯一候选关键字。
五、模式分解
对存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理。
在分解处理中会涉及一些新问题,为使分解后的模式保持原模式所满足的特性,要求分解处理具有无损联接性和保持函数依赖性。
即分解后的关系模式子集,应能通过自然连接运算恢复原状。
1、关系模式规范化时一般应遵循以下原则:
(1)关系模式进行无损连接分解。
关系模式分解过程中数据不能丢失或增加,必须把全局关系模式中的所有数据无损地分解到各个子关系模式中,以保证数据的完整性。
(2)保持原来模型的函数依赖关系。
因为这些函数依赖关系是数据模型反映的客观事物的固有属性,一般是不能舍弃的。
(3)合理选择规范化程度。
考虑到存取效率,低级模式造成的冗余度很大,既浪费了存储空间,又影响了数据的一致性,因此希望一个子模式的属性越少越好,即取高级范式;
若考虑到查询效率,低级范式又比高级范式好,此时连接运算的代价较小,这是一对矛盾,所以应根据情况,合理选择规范化程度。
2、对模式分解的两个基本要求:
模式分解可以提高关系模式的规范化程度,但是必须考虑如下问题:
避免信息丢失:
简单的说,就是模式R分解为R1,R2,…,Rn后,将R1,R2,…Rn自然连接还应该等于模式R。
这就是“无损失联接”准则。
避免数据关系丢失:
简单地说,就是模式R分解为R1,R2,…,Rn后,函数依赖集合F也被对应分解为F1,F2,…,Fn,应满足F与各Fi(i=1,2,…n)的并集等价,即满足F+=(UFi)+。
这就是“保持函数依赖”准则。
关系模式的规范化过程是通过对关系模式的分解来实现的,但是把低一级的关系模式分解为若干个高一级关系模式的方法并不是唯一的。
在这些分解方法中,只有能够保证分解后的关系模式与原关系模式等价的方法才有意义。
3、关系模式分解的三个定义:
(1)分解具有“无损联接性”。
(2)分解要“保持函数依赖”。
(3)分解既要“保持函数依赖性”,又要具有“无损连接性”。
规范化理论提供了一套完整的模式分解算法,按照这套算法可以做到:
●若要求分解具有无损联接性,那么模式分解一定能够达到4NF。
●若要求分解保持函数依赖,那么模式分解一定能够达到3NF,但不一定能达到BCNF。
●若要求分解具有无损联接性又保持函数依赖,则模式分解一定能够达到3NF,但不一定能达到BCNF。
我们希望最好能够既要“保持函数依赖”,又要具有“无损联接性”,从上面结论可以看到只能达到3NF,至于能否达到BCNF或更高,要看具体情况。
这就是在数据库设计中一般采用“基于3NF的数据设计方法”的根本原因。
4、模式设计方法的原则:
关系模式R相对于函数依赖集F分解成ρ={R1,R2,…Rk},应具有以下特性:
(1)ρ中每个关系模式Ri上应有某种范式性质(3NF或BCNF)
(2)无损联接
(3)保持函数依赖集
(4)最小性(ρ中模式个数应最少和模式中属性总数应最少)
一个好的设计方法应符合下列3个原则:
表达性,分离性,最小冗余性。
5、模式分解的算法:
算法一:
把关系模式无损分解成BCNF
输入:
关系模式R和函数依赖集F
输出:
R的一个无损分解ρ={R1,R2,…,Rk}
方法:
设关系模式R(U,F)
(1)置初值:
ρ={R}。
(2)对于关系模式R的分解ρ(初始时ρ={R}),如果ρ中有一个关系模式Ri相对于∏Ri(F)不是BCNF。
由定义可知,Ri中存在一个非平凡FDXY,有X不包含码。
此时把Ri分解成XY和Ri-Y两个模式。
重复上述过程,一直到ρ中每一个模式都是BCNF。
(3)算法结束,ρ就是分解结果。
R(U,F),U=ABCDEF={ABC,BD,DE},码是AB。
分解过程如下:
(1)先分出DE,ρ={R1(ABCD),R2(DE)}
(2)再从R1中分出BD,ρ={R1(ABC),R2(DE),R3(BD)}
(3)R1,R2,R3都属于BCNF,分解完成。
设有关系模式R(U,F),其中:
U={C,T,H,R,S,G}F={CSG,CT,THR,HRC,HSR}
将其无损联接地分解为BCNF。
R上只有一个侯选键HS。
(1)令ρ={CTHRSG}。
(2)ρ中的模式不是BCNF。
(3)考虑CSG,这个函数依赖不满足BCNF条件(CS不包含侯选键HS),将CTHRSG分解为CSG和CTHRS。
计算∏CSG(F)和∏CTHRS(F),前者的最小覆盖是:
CS
G;
后者的最小覆盖是:
CT,HRC,THR,HSR。
模式CTHRS的侯选关键字是HS。
CSG已是BCNF,进一步分解CTHRS。
选择CT,把CTHRS分解成CT和CHRS,计算∏CT(F)和∏CHRS(F),前者的最小覆盖是:
CT;
HCR,HSR,HRC。
模式CHRS的侯选关键字是HS。
CT已是BCNF,再分解CHRS。
选择HCR,把CHRS分解成CHR和CHS,计算∏CHR(F)和∏CHS(F),前者的最小覆盖是:
CHR,HRC;
HSC。
这时CHR和CHS均为BCNF。
(4)ρ={CSG,CT,CHR,CHS}。
(HSR,HSHRHRC=>
HSC)
算法二:
把一个关系模式分解为3NF,使它具有依赖保持性。
关系模式R和R的最小依赖集Fmin。
R的一个分解ρ={R1,R2,…Rk},Ri为3NF(i=1,…,k),ρ具有依赖保持性。
达到3NF保持函数依赖分解的方法:
设关系模式R(U,F):
(1)将F化为最小函数依赖集,令F=Fmin。
(2)把在F中不出现的属性从U中去掉,属性集合仍然为U。
(3)对照F中的函数依赖集,将所有函数依赖左端相同的划为一组,相应的右端以及函数依赖均归入该组。
(4)这些分组就是分解后的模式组成。
(5)这种分解方法得到的就是达到3NF且保持函数依赖的分解。
F={B—>
G,CEB,CA,CEG,BD,CD},码是CE,分解成三个模式。
R1:
U1=BDG,F1={BG,BD}
R2:
U2=ACD,F2={CA,CD}
R3:
U3=BCEG,F3={CEB,CEG}
分解后,R1,R2,R3均达到3NF,且分解符合保持函数依赖的规则。
例2:
设有关系模式R(U,F),其中:
U={C,T,H,R,S,G}F={CSG,CT,THR,HRC,HSR},将其保持依赖性分解为3NF。
(1)求出F的最小依赖集,Fmin={CSG,CT,THR,HRC,HSR}。
(2)无。
(3)R1:
U1=CSG,F1={CSG}
U2=CT,F2={CT}
U3=THR,F3={THR}
U4=HRC,F4={HRC}
U5=HSR,F5={HSR}
(4)ρ={CSG,CT,THR,HRC,HSR}
算法三:
把一个关系模式分解为3NF,使它既具有无损联接性又具有依赖保持性。
①对于关系模式R和R上成立的FD集F,先求出F的最小依赖集,然后再把最小依赖集中那些左部相同的FD用合并性合并起来。
②对最小依赖集中,每个FDXY去构成一个模式XY。
③在构成的模式集中,如果每个模式都不包含R的候选键,那么把候选键作为一个模式放入模式集中。
这样得到的模式集是关系模式R的一个分解,并且这个分界既是无损分解,又能保持FD。
检验无损联接性的方法:
关系模式R(A1,A2,…,An),它的函数依赖集F以及分解ρ={R1,R2,…,Rk}。
确定ρ是否具有无损联接性。
(1)构造一个k行n列的表,若i行对应于关系模式Ri,第j列对应于属性Aj。
如果Aj∈Ri,则在第i行第j列上放符号aj,否则放符号bij。
(2)逐个检查F中的每一个函数依赖,并修改表中的元素。
其方法如下:
取F中一个函数依赖X—>
Y,在X的分量中寻找相同的行,然后将这些行中Y的分量改为相同的符号,如果其中有aj,则将bij改为aj;
若其中无aj,则改为bij。
这样反复进行,如果发现某一行变成了a1,a2,…,ak,则分解ρ具有无损联接性;
如果F中所有函数依赖都不能再修改表中的内容,且没有发现这样的行,则分解ρ不具有无损联接性。
对于上例的关系模式R(U,F),将其无损联接性和依赖保持性分解为3NF。
依据算法:
(1)由上例求出依赖保持性分解为:
ρ={CSG,CT,THR,HRC,HSR}
(2)判断其无损联接性如下图所示:
Ri
C
T
H
R
S
G
CSG
a1
b12
b13
b14
a5
a6
CT
a2
b23
b24
b25
b26
THR
b31
a3
a4
b35
b36
HRC
b42
b45
b46
HSR
b51
b52
b56
(在已知F={CSG,CT,THR,HRC,HSR}
①看CS上相同的,再改G的成分——没有
看C上相同的,再改T的成分——2个a2①
看TH上相同的,再改R的成分——没有
看HR上相同的,再改C的成分——2个a1①
看HS上相同的,再改R的成分——没有
②再看CS上相同的,再改G的成分——有一个a6②
看C上相同的,再改T的成分——有一个a2②,其它未发生变化,略)
a2①
a1①
a2②
a6②
(3)不执行。
(4)由于表中有一行从a1,a2,…,a6全满,由此可知,ρ具有无损联接性,
输出ρ={CSG,CT,THR,HRC,HSR}。
例2:
已知,U={A,B,C,D},F={A—>
B,A-->
C,BC—>
D,D-->
A}
判断一个分解ρ={AB,AC,BCD,DA}是否具有无损联接性。
B
AB
AC
b22
BCD
b41
DA
b43
由于,A—>
B,b22a2,b42a2
A-->
C,b13a3,b23a3,b43a3
BC—>
D,b14a4
D-->
A,b41a1
所以,ρ={AB,AD,BCD,DA}具有无损联接性。
例3:
U={A,C,B},F={A—>
B,C-->
B}
判断一个分解ρ={AC,BC}是否具有无损联接性。
ρ的无损联接性判断结果表如下所示:
由此判断具有无损联接性。
BC
b21
B没有变化,C-->
所以,ρ={AC,BC}具有无损联接性。
例4:
设有关系模式R(A,,B,C,D),其上的函数依赖集:
F={A→C,C→A,B→AC,D→AC}
(1)计算(AD)+。
(2)求F的最小等价依赖集Fm。
(3)求R的关键字。
(4)将R分解使其满足BCNF且无损连接性。
(5)将R分解成满足3NF并具有无损连接性与保持依赖性。
(1)令X={AD},,X(0)=AD,X
(1)=ACD,X
(2)=ACD,故(AD)+=ACD。
(2)将F中的依赖右部属性单一化:
A→CC→A
F1=B→A
D→A
在F1中去掉多余的函数依赖:
∵B→A,A→C∴B→C是多余的。
又∵D→A,A→C∴D→C是多余的。
F2=B→AD→A
函数依赖集的最小集不是惟一的,本题中还可以有其他答案。
∵F2中所有依赖的左部却是单属性,∴不存在依赖左部有多余的属性。
∴
Fˊ=B→AD→A
(3)∵BD在F中所有函数依赖的右部均未出现,∴候选关键字中一定包含BD,而(BD)+=ABCD,因此,BD是R惟一的候选关键字。
(4)考虑A→C,∵AC不是BCNF(AC不包含候选关键字BD),将ABCD分解为AC和ABD。
AC已是BCNF,进一步分解ABD,选择B→A,把ABD分解为AB和BD。
此时AB和BD均为BCNF,∴ρ={AC,AB,BD}。
(5)由
(2)可求出满足3NF的具有依赖保持性的为ρ={AC,BA,DA}。
判断其无损连接性如图4.10所示的表,由此可知ρ不具有无损连接性。
令ρ=ρ∪{BD},BD是R的候选关键字,∴ρ={AC,BA,DA,