完整版概率论与数理统计知识点总结Word格式.docx
《完整版概率论与数理统计知识点总结Word格式.docx》由会员分享,可在线阅读,更多相关《完整版概率论与数理统计知识点总结Word格式.docx(23页珍藏版)》请在冰豆网上搜索。
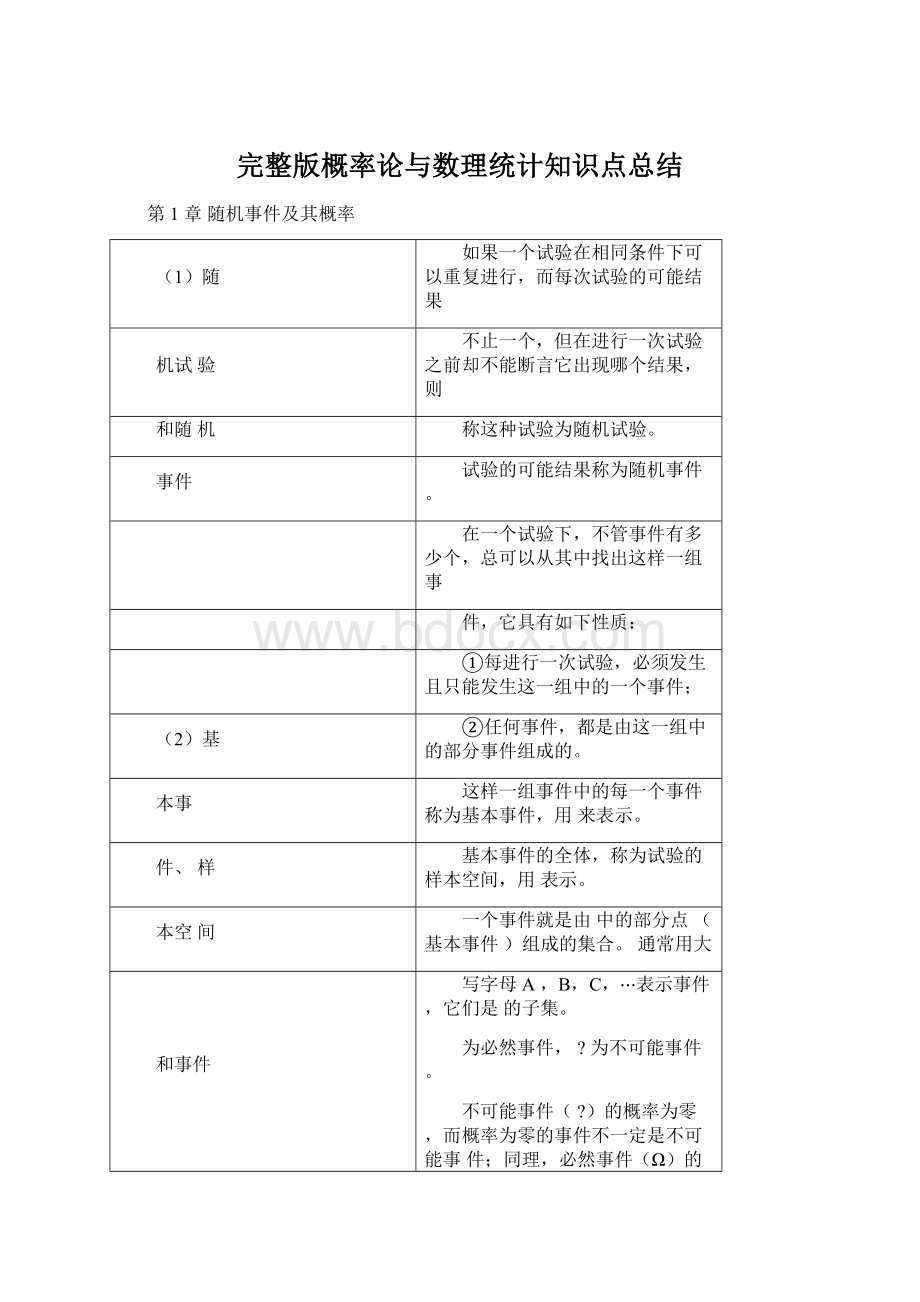
(AB)∪C=(A∪C)∩(B∪C)(A∪B)∩C=(AC)∪(BC)
AiAi
德摩根率:
i1i1ABAB,ABAB
(4)概率的公理化定义
设为样本空间,A为事件,对每一个事件A都有一个实数P(A),若满足下列三个条件:
1°
0≤P(A)≤1,
2°
P(Ω)=13°
对于两两互不相容的事件A1,A2,⋯有
PAiP(Ai)
i1i1则称P(A)为事件A的概率。
(5)古典概型
1,2n,
2°
P
(1)P
(2)P(n)1。
n
设任一事件A,它是由1,2m组成的,则有P(A)=
(1)
(2)(m)=P
(1)P
(2)P(m)
mA所包含的基本事件数n基本事件总数
(6)几何概型
若随机试验的结果为无限不可数并且每个结果出现的可能性均匀,同时样本空间中的每一个基本事件可以使用一个有界区域来描述,则称此随机试验为几何概型。
对任一事件A,P(A)L(A)。
其中L为几何度量(长度、面积、体积)。
L()
(7)加法公式
P(A+B)=P(A)+P(B)-P(AB)
当AB不相容P(AB)=0时,P(A+B)=P(A)+P(B)
当AB独立,P(AB)=P(A)P(B),P(A+B)=P(A)+P(B)-P(A)P(B)
(8)减法公式
P(A-B)=P(A)-P(AB)
当BA时,P(A-B)=P(A)-P(B)当A=Ω时,P(B)=1-P(B)
(9)条件概率
定义设A、B是两个事件,且P(A)>
0,则称PP((AAB))为事件A发生P(A)条件下,事件B发生的条件概率,记为P(B/A)PP((AAB))。
P(A)条件概率是概率的一种,所有概率的性质都适合于条件概率。
例如P(Ω/B)=1P(B/A)=1-P(B/A)
(10)乘法公式
乘法公式:
P(AB)P(A)P(B/A)更一般地,对事件A1,A2,⋯An,若P(A1A2⋯An-1)>
0,则有
P(A1A2⋯An)P(A1)P(A2|A1)P(A3|A1A2)⋯⋯P(An|A1A2⋯An1)。
(11)独立性
①两个事件的独立性
设事件A、B满足P(AB)P(A)P(B),则称事件A、B是相互独立的。
若事件A、B相互独立,且P(A)0,则有
P(AB)P(A)P(B)
P(B|A)P(B)
P(A)P(A)
若事件A、B相互独立,则可得到A与B、A与B、A与B也都相互独立。
必然事件和不可能事件?
与任何事件都相互独立。
?
与任何事件都互斥。
②多个事件的独立性
设ABC是三个事件,如果满足两两独立的条件,
P(AB)=P(A)P(B);
P(BC)=P(B)P(C);
P(CA)=P(C)P(A)并且同时满足P(ABC)=P(A)P(B)P(C)那么A、B、C相互独立。
对于n个事件类似。
(12)全概公式
设事件B1,B2,,Bn满足
1°
B1,B2,,Bn两两互不相容,P(Bi)0(i1,2,,n),
ABi
i1,则有
P(A)P(B1)P(A|B1)P(B2)P(A|B2)P(Bn)P(A|Bn)。
全概率公式解决的是多个原因造成的结果问题,全概率公式的题型:
将试验可看成分为两步做,如果要求第二步某事件的概率,就用全概率公式;
(13)贝叶斯公式
设事件B1,B2,⋯,Bn及A满足
B1,B2,⋯,Bn两两互不相容,P(Bi)>
0,i1,2,⋯,n,
i1,P(A)0,
则
P(Bi/A)nP(Bi)P(A/Bi),i=1,2,⋯n。
P(Bj)P(A/Bj)
j1
此公式即为贝叶斯公式。
P(Bi),(i1,2,⋯,n),通常叫先验概率。
P(Bi/A),(i1,2,⋯,n),通常称为后验概率。
贝叶斯公式反映了“因果”的概率规律,并作出了“由果朔因”的推断。
将试验可看成分为两步做,如果求
在第二步某事件发生条件下第一步某事件的概率,就用贝叶斯公式我们作了n次试验,且满足
每次试验只有两种可能结果,A发生或A不发生;
(14)伯努利概型
n次试验是重复进行的,即A发生的概率每次均一样;
每次试验是独立的,即每次试验A发生与否与其他次试验A发生与否是互不影响的。
这种试验称为伯努利概型,或称为n重伯努利试验。
用p表示每次试验A发生的概率,则A发生的概率为1pq,用Pn(k)
表示n重伯努利试验中A出现k(0kn)次的概率,
Pn(k)Cknpkqnk,k0,1,2,,n
第二章随机变量及其分布
1)设离散型随机变量X的可能取值为Xk(k=1,2,⋯)且取各个值的概率,
即事件(X=Xk)的概率为P(X=xk)=pk,k=1,2,⋯,则称上式为离散型随机变量X的概率分布或分布律。
有时也用分布列的形式给出:
X|x1,x2,,xk,P(Xxk)p1,p2,,pk,。
显然分布律应满足下列条件:
pk1
1)pk0,k1,2,,
(2)k1
2)设F(x)是随机变量X的分布函数,若存在非负函数f(x),对任意实数
x,有
x
F(x)f(x)dx,
则称X为连续型随机变量。
f(x)称为X的概率密度函数或密度函数,简称概率密度。
密度函数具有下面4个性质:
分布1、f(x)0
x2
3、P(x1Xx2)F(x2)F(x1)2f(x)dx
x1
4、P(x=a)=0,a为常数,连续型随机变量取个别值的概率为0
(3)
设X
为随机变量,x是任意实数,则函数
分布
F(x)
P(Xx)
函数
称为随机变量X的分布函数,本质上是一个累积函数。
P(a
Xb)F(b)F(a)可以得到X落入区间(a,b]的概率。
分布函
数F(x)表示随机变量落入区间(–∞,x]内的概率。
分布函数具有如下性质:
0F(x)1,x;
F(x)是单调不减的函数,即x1x2时,有F(x1)F(x2);
3°
F()limF(x)0,F()limF(x)1;
xx
4°
F(x0)F(x),即F(x)是右连续的;
5°
P(Xx)F(x)F(x0)。
对于离散型随机变量,F(x)pk;
xkx
x对于连续型随机变量,F(x)f(x)dx。
(4)
0-1分
P(X=1)=p,P(X=0)=q
六大
布
二项分
在n重贝努里试验中,设事件A发生的概率为p。
事件A发生
的次数是随机变量,设为X,则X可能取值为0,1,2,,n。
P(Xk)Pn(k)Cnkpkqnk,其中q1p,0p1,k0,1,2,,n,
则称随机变量X服从参数为n,p的二项分布。
记为
X~B(n,p)。
当n1时,P(Xk)pkq1k,k0.1,这就是(0-1)分布,所
以(0-1)分布是二项分布的特例。
泊松分
设随机变量X的分布律为
k
P(Xk)e,0,k0,1,2,k!
则称随机变量X服从参数为的泊松分布,记为X~()或者P()。
泊松分布为二项分布的极限分布(np=λ,n→∞)。
均匀分
设随机变量X的值只落在[a,b]内,其密度函数f(x)在[a,1
b]上为常数1,即
ba
1,a≤x≤b
f(x)0b,a其他,
则称随机变量X在[a,b]上服从均匀分布,记为X~U(a,
b)。
分布函数为
0,x<
a,
xa
baa≤x≤b
F(x)f(x)dx
1,x>
b。
当a≤x1<
x2≤b时,X落在区间(x1,x2)内的概率为
x2x1
P(x1Xx2)21。
指数分
xe,x0,f(x),
0,x0,
其中0,则称随机变量X服从参数为的指数分布。
正态分
设随机变量X的密度2函数为
(x)2
f(x)
122
e2,x,
2
其中、
0为常数,则称随机变量X服从参数为、的2
正态分布或高斯(Gauss)分布,记为X~N(,)。
f(x)具有如下性质:
f(x)的图形是关于x对称的;
当x
时,f()1为最大值;
22
若X~N(
2),则X的分布函数为
F(x)21
xe(t22)2dt
参数
0、1时的正态分布称为标准正态分布,记为
X~N(0,1)1,其x密2度函数记为
(x)
2e2,x,
分布函数为xt2
(x)12
e2dt。
(x)是不可求积函数,其函数值,已编制成表可供查用。
Φ(-x)=
1-Φ(x)且Φ(0)=1。
如果X~
2X2
N(,2),则X~N(0,1)。
P(x1X
x2)21。
(6)
下分位表:
P(X
)=;
分位
上分位表:
)=。
数
(7)
离散型
已知X的分布列为
X
x1,x2,,xn,
P(X
xi)p1,p2,,pn,
Yg(X)
的分布列(yig(xi)互不相等)如下:
的分
Y
g(x1),g(x2),,g(xn),,
布函
P(Yyi)若有某些i
g(xi)相等,则应将对应的pi相加作为g(xi)的概率。
连续型
先利用
X的概率密度fX(x)写出Y的分布函数FY(y)=
P(g(X)≤
y),再利用变上下限积分的求导公式求出fY(y)。
第三章二维随机变量及其分布
(1)联离散型
合分布
如果二维随机向量(X,Y)的所有可能取值为至多可列个有序对(x,y),则称为离散型随机量。
设=(X,Y)的所有可能取值为(xi,yj)(i,j1,2,),且事件{=(xi,yj)}的概率为pij,,称P{(X,Y)(xi,yj)}pij(i,j1,2,)
为=(X,Y)的分布律或称为X和Y的联合分布律。
联合分布有时也用下面的概率分布表来表示:
YX
y1
y2
⋯
yj
p11
p12
p1j
p21
p22
p2j
xi
pi1
pij
这里pij具有下面两个性质:
1)pij≥0(i,j=1,2,⋯);
2)pij1.
ij
对于二维随机向量(X,Y),如果存在非负函数f(x,y)(x,y),使对任意一个其邻边分别平
行于坐标轴的矩形区域D,即D={(X,Y)|a<
x<
b,c<
y<
d}有
P{(X,Y)D}f(x,y)dxdy,
D
则称为连续型随机向量;
并称f(x,y)为=(X,Y)的分布密度或称为X和Y的联合分布密度。
分布密度f(x,y)具有下面两个性质:
(1)f(x,y)≥0;
(2)f(x,y)dxdy1.
2联合
设(X,Y)为二维随机变量,对于任意实数x,y,二元函数
F(x,y)P{Xx,Yy}
称为二维随机向量(X,Y)的分布函数,或称为随机变量X和Y
的联合分布函数。
分布函数是一个以全平面为其定义域,以事件
{(1,2)|X
(1)x,Y
(2)y}的概率为函数值的一个实值函数。
分布函数F(x,y)具有以下的基本性质:
(1)0F(x,y)1;
(2)F(x,y)分别对x和y是非减的,即
当x2>
x1时,有F(x2,y)≥F(x1,y);
当y2>
y1时,有F(x,y2)≥F(x,y1);
(3)F(x,y)分别对x和y是右连续的,即
F(x,y)F(x0,y),F(x,y)F(x,y0);
(4)F(,)F(,y)F(x,)0,F(,)1.
(5)对于x1x2,y1y2,
P(x1<
x≤x2,y1<
y≤y2)=F(x2,y2)F(x2,y1)F(x1,y2)F(x1,y1)0
3边缘
离散型X的边缘分布为
Pi?
P(Xxi)pij(i,j1,2,);
j
Y的边缘分布为
P?
jP(Yyj)pij(i,j1,2,)。
i
X的边缘分布密度为fX(x)f(x,y)dy;
Y的边缘分布密度为fY(y)f(x,y)dx.
4条件分布
在已知X=xi的条件下,Y取值的条件分布为pij
P(Yyj|Xxi)ij;
pi?
在已知Y=yj的条件下,X取值的条件分布为pij
P(Xxi|Yyj)ij,
p?
在已知Y=y的条件下,X的条件分布密度为f(x,y)
f(x|y);
fY(y)
在已知X=x的条件下,Y的条件分布密度为f(x,y)
f(y|x)
fX(x)
5独立性
一般型
F(X,Y)=FX(x)FY(y)
pijpi?
p?
有零不独立
f(x,y)=fX(x)fY(y)直接判断,充要条件:
①可分离变量②正概率密度区间为矩形
二维正
态分布
1x12(x1)(y2)y2
12(12)1122
f(x,y)12e,
21212
=0
随机变量的函数
若X1,X2,⋯Xm,Xm+1,⋯Xn相互独立,h,g为连续函数,则:
h(X1,X2,⋯Xm)和g(Xm+1,⋯Xn)相互独立。
特例:
若X与Y独立,则:
h(X)和g(Y)独立。
例如:
3X+1和5Y-2独立。
6二维均匀分布
设随机向量(X,Y)的分布密度函数为
1(x,y)D
SD
f(x,y)
0,其他
其中SD为区域D的面积,则称(X,Y)服从D上的均匀分布,记
为(X,Y)~U(D)。
图3.2
7正态
1x12(x1)(y2)y2
12(12)1122
2e,
1212
其中1,2,
10,20,||1是5个参数,则称(X,Y)服从二维正
态分布,
记为(X,
Y)~N(1,2,12,22,).
由边缘密度的计算公式,可以推出二维正态分布的两个边缘分布仍
为正态分布,
即X~N(
1,12),Y~N(2,22).
但是若X~
N(1,12),Y~N(2,22),(X,Y)未必是二维正态分布。
8函数
Z=X+Y
根据定义计算:
FZ(z)P(Zz)P(XYz)
的分布
对于连续型,fZ(z)=f(x,zx)dx
两个独立的正态分布的和仍为正态分布(12,1222)。
n个相互独立的正态分布的线性组合,仍服从正态分布。
Cii,2Ci2i2
iiiiii
Z=max
若X1,X2Xn相互独立,其分布函数分别为
min(X1
Fx1(x),Fx2(x)Fxn(x),则Z=max,min(X1,X2,⋯Xn)的分布
X2,⋯
函数为:
Xn)
Fmax(x)Fx1(x)?
Fx2(x)Fxn(x)
Fmin(x)1[1Fx1(x)]?
[1Fx2(x)][1Fxn(x)]
第四章随机变量的数字特征
(1)一
维随机
期望
设X是离散型随机
设X是连续型随机变量,其概率密
变量的
期望就是
变量,其分布律为
度为f(x),
数字特
平均值
P(Xxk)=pk,
E(X)xf(x)dx
征
k=1,2,⋯,n,
E(X)xkpk
k1
(要求绝对收敛)
函数的期
Y=g(X)
望
E(Y)g(xk)pk
E(Y)g(x)f(x)dx
方差
D(X)=E[
X-E(X)]2
标准差
D(X)[xkE(X)]2pk
D(X)[xE(X)]2f(x)dx
(X)D(X)
(2)期
(1)E(C)=C
望的性
(2)E(CX)=CE(X)
质
(3)E(X+Y)=E(X)+E(Y)
nn
,E(CiXi)CiE(Xi)
i1i1
(4)E(XY)=E(X)E(Y),充分条件:
X和Y独立;
充要条件:
X和Y不相关。
(3)方
(1)
D(C)=0;
E(C)=C
差的性
(2)
D(aX)=a2
D(X);
E(aX)=aE(X)
D(aX+b)=a
2D(X)
E(aX+b)=aE(X)+b
D(X)=E(X
2)-E2(X)
(5)
D(X±
Y)=D(X)+D(Y)
,充分条件:
X和Y独立;
X和Y不相关。
±
2E[(X-E(X))(Y-E(Y))],无条件
成立。
而E(X+Y)
=E(X)+E(Y)
,无条件成立。
B(1,p)
p
p(1p)
B(n,p)
np
np(1p)
泊松
P()
(4)常
U(a,b)
ab
(ba)2
12
见分布
指数
1
的期望
和方差
e()
N(,2)
(5)二维随机变量的
E(X)xipi?
i1
E(Y)yjp?
E(X)xfX(x)dx
E(Y)yfY(y)dy
E[G(X,Y)]=
的期
G(xi,yj)pijij
G(x,y)f(x,y)dxdy
D(X)[xiE(X)]2pi?
D(X)[xE(X)]2fX(x)dx
D(Y)