半角模型旋转变换几何练习Word文件下载.docx

半角模型旋转变换几何练习Word文件下载.docx

《半角模型旋转变换几何练习Word文件下载.docx》由会员分享，可在线阅读，更多相关《半角模型旋转变换几何练习Word文件下载.docx（24页珍藏版）》请在冰豆网上搜索。

•

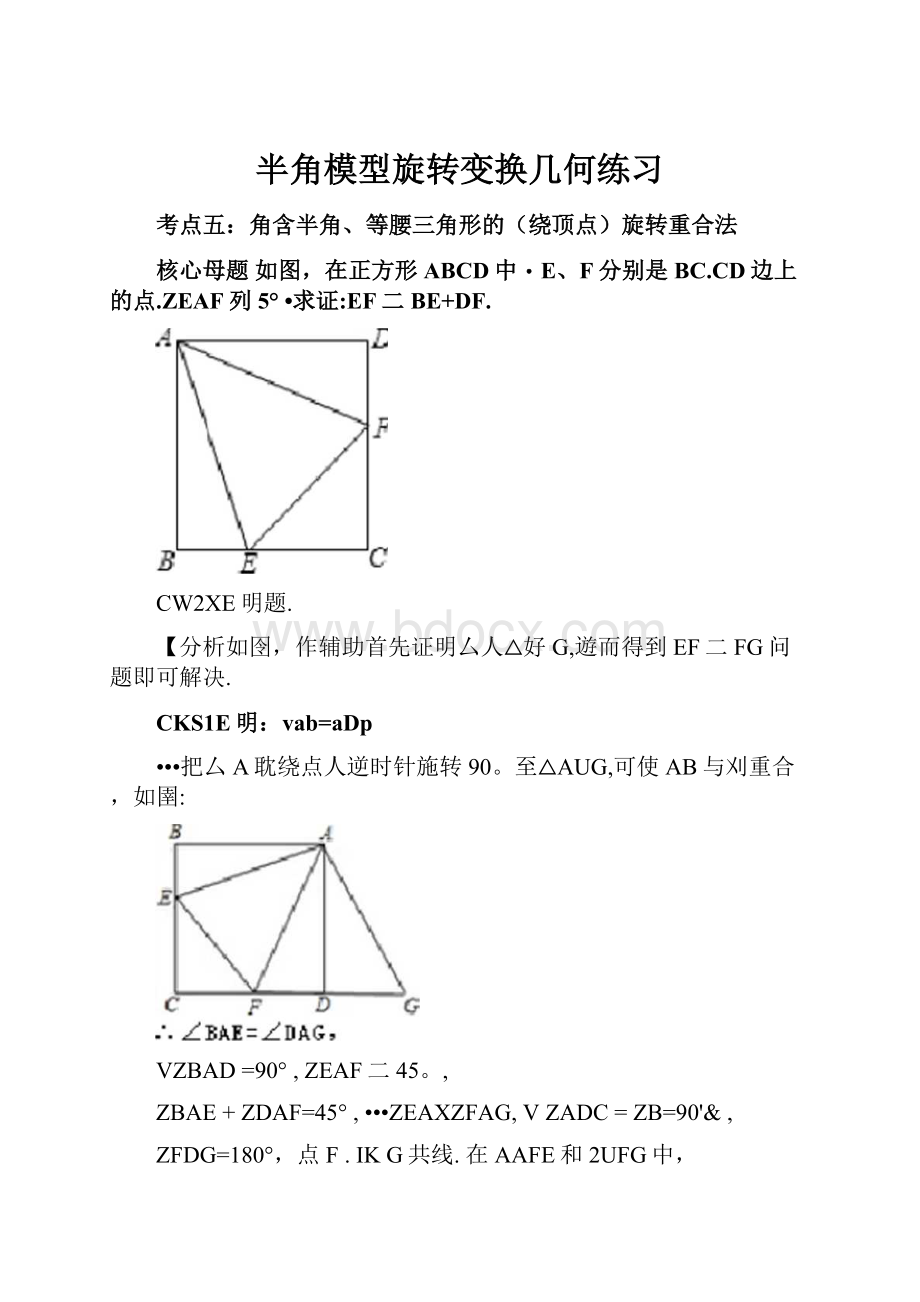
/.ZEAF=45°

.

【点评苹题考查了全等三角形的判走，考察了全等三角形对应角相等的性质，本题中求证AAJE^AkFK是解题的关健.

变式二：

如图，在正方形ABCD中，E、F分别是BC、CD边上的点，ZEAF=45°

AG丄EF,求证：

AG=AB.

【考点就转的性质,全等三角形的判走与性质,正方形的性质•

【专題证明题.

【分析洗根据正方形的性质箒吩AD,ZBAT=90°

则可杷△ADE续点晰时軒施转90。

得到△ABQ,如圉，根拥施转的性质得AQ=AE,ZEAQ=90Q,ZABQ=ZD=90°

则可判断点Q在CB的延长线上，由ZEAF二45。

得到Z&

Af二90。

-ZEAF二屿°

然后根据叱判断△AFQWZiAFE.得到FQ=FE,再根拥全等三角形对应边上的高相等得到结论.

【第咅证明：

丫四边形ABCD为正方形，

AAB=AD,ZBAJ=90°

.•.把△ADE绕点A顺时针社转90°

得S'

JAABQ,如囹,

AAQ=AE,ZIAQ=9O°

ZABQ=ZH=90°

而ZABC=90°

•••空Q在CB的延长线上，

•••ZEAF=45°

AZQAF=90°

-ZEAF=45°

AZEAF=ZQAF,

在AATQ和AAFE中，

fAF^AF

｛乙QAF=ZEAF,

AAFQ^AAFE（SAS〉,

afq=fe5

VAB±

FQ»

AG丄FE,

••-AB-AG・

【点评茸题考查了旋转的性质：

对应点到血转中心的距鬲相等；

对应点与就转中心所连线段的夹角等于旋转角；

验转前、后的囹形全等.也考查了全等三角形的判定与性质・正方形的性质.

综合：

在正方形宓9中，若弘片分别在边应；

仞上移动，且满足MN=BM+ZZV；

求证：

©

.^MAN=^®

.C^cwv=2AB®

.AM.4V分别平分刁tfV和ZDNM.

练习

1、如图，在四边形ABCD中，AB=BC,ZA=ZC=90°

ZB二135°

K、N分别是AB、BC上的

点，若△BKN的周长是AB的2倍，求ZKDN的度数？

2、己知：

正方形ABCD中，ZMAN=45°

ZMAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点'

I、N.当ZMAN绕点A旋转到BM=DN时（如图1）,易证BM+DN二MN・

（1）当ZMAN绕点A旋转到BMHDN时（如图2）,线段BM、DN和MN之间有怎样的数量关系？

写出猜想，并加以证明；

（2）当ZMAN绕点A旋转到如图3的位遂时，线段BM、DN和MN之间又有怎样的数量关系？

请直接写出你的猜想.

【考点】龍转的性质；

全等三角形的判定2性质；

【分析】

（1）BM^DN=WN咸立，证得B、E、M三点共线即可得到△AEM^AANM＞从而证得ME=MN.

（2）DN-BM=MN・证明方法与

（1）类并

K解苔】解：

（1）BM+DNMN成立•

证明：

如图，吃AADN线点AI帧旳针谁转90。

，

猬到AAEE.则可证得E、B、M三点共线（图形瓯正确）・

ZEAM=90°

-ZKAM=90o-45°

=45°

>

又VZNAM=45°

）

AE=AN

Zeam=Anam

AM=AM

•••△AEM空△ANM〈SAS），

・•・ME-MN^

•••ME=BE4-BM=DN+EM，

ADn+BM=MN；

（2）DM-BM=MN・

右线段DN上载取DQ=BM，右ZiADQ与AABM中，

1AD=AB

Z-ADO-AaBM»

DQ=BM

AAADQSAABM（SAS），

••・NDAQ二ZtAM，

AZQAW=ZNAN.

15^AMN^flAAQN4>

AO=AM

ZQAN=Z3L4X

AN=AN

AAAMN^AAQN（SAS），••・MN=QN，

・・・DNBM=MN・

【点评】本题考查了族转的性质，解决此类问题的关键是正礦的利用施转不变蛍.

3.如图，在四边形ABCD中，AB=AD-ZB+ZD二180°

•E、F分别是边BC.CD上的点，且2

ZEAF二ZBAD,

（1）求证：

EF二BE+FD

（2）如果E、F分别是边BC、CD延长线上的点，共他条件不变，结论是否仍然成立？

说明

理由。

B

D

C

（1）延长CB至阳，使BM=DF,连按Wb证/LADF^AABM,iJAFAE^AMAE,即可得出營案；

囹1

®

2

（2）在CB上截取BM二DF,连接AM,证厶ABM^AADF,推出AF=AM,ZDAF=ZBAM,求出ZEA»

4=^EAF,证厶FAE^AMAE,推出EF二EM即可.

【解音】

（1〉证明：

延长CB至M,使BM=DF,连接⑷

9

•••ZABC+ZD=180°

ZABC4-ZABM=180°

•••ZD=ZA.BM,

在厶ABM^flAADF中，

{AB-AD

zabm=zz>

BM=DF

AABM^AADF（SAS）,

••・AF二AM,ZDAF=ZBAf^

•・•ZBAD=22EAF,

•••ZDAF+ZBAE=ZEAF,

•••ZEAB+ZBAM=ZEAM=ZEAF,在AFAE和△MAE中，fAE=AE

<

ZFAE=ZX/AE，

"

F=AM

/.AJAE^ANAE（SIS）,•••EF=EM=BE+BM=BE+DF,

即EF=BE+DF.

（2）解：

EF、BExDF之间的关系是EF=BE-DF,

理由是：

在CB上荀取B壯DF,连接AM,

TZABC+ZD=180°

ZADC+ZADF=180^,

.•.ZABC=ZkDF,

在AABM和AADF中，

I

AB—AD

0=GDF

BM=DF

AAABM^AADF（SAS）>

•••AF二AN,ZDkF=ZBAMw

TZBAD=2ZEAF=2（ZEADIZDAF）=2（ZEAD+-ZBAM）=ZEAF+（ZEAD+ZBAN）

ZBAD=（ZBAM+ZEAD）+ZMAE

•••ZFUE二ZEAF在△映和MAE中，

'

AE=AE

s/FA£

=ZS£

AE，

.AF=AAf

AFAESAMAE<

5AS）・

.•.EF=EM=BE-BM=BE-DF5

即EF=BE-DF.

5、如图所示，在五边形ABCDE中，AB二AE・BC+DE二CD.ZABC+ZAED=180°

求证：

AD平分ZCDE.

【分析】连接AC,延长DE到厂使EJ=BC,连接疑，易证△店（:

丝AAEF,进而可以证明AACD旦△AFD,可得ZAJSZADF即可解题.

【笛舍】解：

连接延长切到F,使EF=BC,连接AF,

ACD=FD,

•・•ZABC+ZAED二180°

ZA.EF+ZAED=180°

■/.ZABC=ZAEF,

在ZkABI：

和AAEF中，

（AB^.4E

Z.4JC=^AEF，

[3C=EF

/.AABC^AAEF（SAS）,

•••AC=AF,

在△肌11和厶AFD中，

\AC^AF

CD=F2>

\AD^AD

Aacb^Aafd（sss）

AZADC=ZADFJ

即AD平分ZCBE.

6、如图，已知AB二CD二AE二BODE二2.ZABC二ZAED二90°

求五边形ABCDE的面积.

K考点】金等三角形的刘走与性质.

【专題】应用题•

K分析】可延长叹至F,使EF=BCt可得△ABC经△AEF,连AC,AD,AF,可将五边形ABCDE的面秩转化为两个△ADF的面秋，进而求出结论.

延长哑至F,使EF=BC,连AC,AD,AF,

kB=CD=XE=BC+DE,ZABC=ZAED=90°

£

y:

.•.CD=EF+DE=DF,\//

在厶ABC与△AEF中，H£

厶43C=AEF

SC=EF

AkBC^AAEF（SAS>

•••kC=lFi

在△丸CD与△AFD中.

AC=AT

•aCD=DF

AD■AD

AkCD^AAFD（SSS）,

K点评】本题主要考查了全等三角形的判定及性质以及三角形面稅的计算，应憩练塁握•

7、如图1.在四边形ABCD中.AB=AD>

ZB+ZD=180°

E、F分别是边BC、CD上的点，且ZBAD=2ZEAF.

EF二BE+DF；

（2）在

（1）问中，若将AAEF绕点A逆时针旋转，当点E、F分别运动到BC、CD延长线上时，如图2所示，

试探究EF、BE、DF之间的数最关系.

［考点】全等三角形的判走与性质.

（1）述长CB至乩使BM=DF,逹接M，证厶ADF^AXBM,证厶FXE丝△MAE,即可得出答案：

ffil

BB2

（2）往CB上载取时二DF,连接AM,证4kBM^AADF,推出AJ二AM,ZDAF=ZBAM,求出ZEM=ZEAFj证ZXFAE空△MAE》推出EF二EM即可.

1銀音】

（1）证明：

3S-KCB至叭使BN1二DF.连接

Alfl,

TZABC+ZD=180°

ZABC+ZA.BM=180

。

•••ZD=ZABM,

在△ABM和ZkADF中，

（AS=AD

iZABXf=S

\3M^DF

・•・AABM^AADF（SAS）,

AF=AM,2DAF=ZBAM,

•••ZBAD=2ZEAFj

•••ZDAF+ZBAE=ZEAF?

•••ZEAB+ZBAN=ZEAM=ZEAF,在△FAE和△MAE中，

（A£

=AE

ZF.QE=^XL4£

{AF=AU

•••△FAE竺△MAE（SAS）,

••・EF=EM=BE-FBM=BE+DF.

即EF=BE+UF.

（2）®

：

EF、BE、DF之间的关系是EF=BE-DF,

谨由是：

在CB上截取胡二UF,连接刖，

TZABC4ZD=180^,ZADC+ZADF=L80Q,

ZABC=ZADT>

在△ABM和△人DF中，

（A3=AD

{Z^="

DF

[3Xf=DF

.•.AABM^AADF（SAS）,

AF=kM,ZD1F=ZBAM,

TZBAD=2ZEAF=2（ZEADfZDAF）=2（ZEMJ+ZBAN）=ZEAT+（ZEAB+ZBAM）又•••ZBAD二（ZBAM+/EAD）4ZNAE

•••ZNAE=ZEAJ在AFAE和△MAE中,

（AE=AE

^FA£

=S£

=AV

/.AFAE^AMAE（SAS）•

.•.EF=EM=BE-BM=BE-DF,

8.如图，在AABC中.ZACB二90°

AC二BC,P是ZkABC内一点，且PA二3,PC=2,PB=1.求ZBPC的度数

K鮮咨】解：

过点C作ED丄C"

使CD=CF=2,连接CD,口，AB,

7Z14-Z2=ZACB=90°

=ZDCP=Z3+Z2,

；

•Z1=Z3>

在和ZkCBP中，

{CD=CP

Z3=Z1,

[ac^bc

/.ACAD^ACBP（SAS）■

•••DA=PB=1,ZADC=NBPC,在等腰RtADCF中，Z4=45°

根据勾股定理得:

DP2=CD2+CF2=22+22=8i

VDP5+D*.2=8+1=9»

AP2=32=9w

/.dp2+di2=ap2,

•••△ADF为直角三角形，即/5詣0°

则ZBFC=ZkDC=Z4+Z5=45<

>

十90。

二135°

K分析】过贞C作CD丄CF・使CD=CP=2t连接CD,PD,AD,根lgAC=BC,由同角的余角相等得到夹角相等，利用SAS的三角形ACD与三角形CBP全等，利用全等三角形对应边相等，对应角相等得到AZADC=ZBPC,在直角三角形DCF中，利用勾股定理求出DP的长，由AD以及AF的长，利用勾股定理的逆定連得到三角的ADP为直角三角形，由Z4+Z5求出ZADC度数，即为ZBPC度数•

半角模型

2=丄0且&

+厂=180。

.条件：

2

思路：

（IX延长其中一个补角的线段

（延长切到E,使ED=BM,连M或延长6®

到尺使FB=DN,连M）

思路:

分别将和△/!

/）“以AM和AN为对称轴翻折，但一定要证明

M、P.N三点共线.S+S=180P且ab=AD）

例题应用：

例1、在正方形傲②中，若M、N分别在边Q?

上移

动，且满足0^诙+皿求证：

①・/WAN=45。

.AM.创分别平分和NZWM.

思路同上略.

②.求证：

AB=AH.

例1拓展：

在正方形ABCD中，已知ZMAN^,若M、N分别在边

例2•在四边形的⑦中，NB+N©

=18『，AB二AD,若E、尸分别在边

如4皿

CB、”的延长线上移动，

①•试探究线段椒BM、ZW之间的数量关系.

BC、CD匕且满足耶疥+莎求证:

练习巩固：

如图，在四边形個⑦中，NB=N»

=90。

，AB=AD9若e、

^AF=-^BAD.

F分别在边切上的点，且2.求证：

EF=BE+DF.

半角

例题：

如图，将绕点（?

颤时针旋转90°

得心£

）,连结MD,贝UAD=BN"

tCD=CN."

CD=ZBCN■・••^MCD^ZACM+ZACD

=ZACM+ZBCN

-90°

-45°

-ZWV.

AAMDC^AMNC.

AW=A£

V=x

又易得ZO4A/=45o+45o=90°

••在RlA/LW3中■有/w2+n2=x1■故应选（B）

练习：

1.如图■正方形価8的边长为1■個、・<

/>

上各存一点几Q.若"

％的周长为2,求"

C。

的度数・

Q

2.E、F分别是正方形/BCD的边8匚CD上的点■且Z£

XF»

45°

AllLET,〃为垂足,求证:

AH=AB•

3.如图所示.在等腰直角△购C的斜边肋上取两点M.N■使ZAfCV=45。

■记AM=m,MN=x■BN=n.求证：

以「m.”为边长的三角形的形状是直角三角形.

4已知：

如图1在RtUSU中...AB^AC•点d£

分别为耀段PC上两动点•若^£

UE=45°

•探究线段BZXDE、比三条氏段之间的数JB关系.

小明的思路是:

绕点/!

顺对针旋转2,得到£

砧，连结ED,

使问题得到解决.请你參考小明的思路探究并解决下列问融:

⑴狷想妙、DE、EC三条线段之间存在的数量关系式，并对你的猜想给子证明；

⑵当动点£

仕线段眈上，动点D运动枉线段C址长线上时，如图2,具它条件不变,⑴中琛究的结论是合友生改变？

谴说明你的猜想并给予证明.

ffl）

m2

解析：

X如图•正方形的边长为1,AB.Q上各存一点P.Q,若的周长为2,求ZPC0的度数解：

把MDp绕点C•旋转90°

到ACF的位置.CQ=CF•

VAQ+AP+QP^2t又・40+QDTP+M=2•「QD7P=QP・又DQ=BFt

:

.AQCPmZCP.

・4CPn"

（JP•又ZpCF=90°

・・"

CQ=45。

•

2、E.F分别是正方形ABCD的边BC\CD上的点■且ZE4^=45°

AllLEFfH为垂足，求证:

AllAB.

ZB人G-ZDAF.AG^AF.

再证厶4£

0空2少.

全等三角形的对应高相等

俐用三角形全等可证得）・则有AH^AB・

M

/N

3.如图所示•在等接宜角3C的料边M上取两点M.Vf使厶心=45°

■记AM^m.MN=x,BN=n,求证：

以I”、”为边长的三角形的形状見直角三角形.

解：

法1：

如图所示，将M8V绕点CI6时针濮转90°

.得

连按.观AD=BN=ntCDYN.ZACD^^BCNt

故3CD-ZACM♦ZACD^ZACM十ZBCN-9（T-45°

-45°

-ZMCN从而AMDC^AMNC.

8!

J.WD=MV=x.

而么皿/■45。

+45°

・900•

故布盲角三角形MW7）中有m24-r2=t2.

法2:

我们用上一讲学习过的"

对称变换"

也能得到認答•如图所示■以为对称轴将ATM觀折到AQ”P的伫曹・易证和MEN天于GV对称，目APM\为直角三角形,并且可得/=A\f=m.PN=NB=rt9MN=x・

4.已知：

如图1在RIA4M中./R4C=5,AH^AC.点D.£

分别为线段阳上两前点，若//14£

=45°

•探究线段血、BL、£

1三条线段之间的数圧关系.

小明的恩路是:

把绕点.4颇时针旋转2,得到A4砂,连结FD.

便问题得到屛决.请你拓考小明的思路琛究开解决下列问题:

⑴猜想购、IX、EC三条线段之间存在的数屋关系式，并对你的券想给予证明；

（2）当动点£

住线段上，动点D运动住线段CB延长线上时，如匿2，其它条件不变，⑴中探究的结论是臼友生改变？

请说明你的猜粗并给予证明・

Wi

（1）D^^BD^EC2

根据S4EC绕点A顺时针族转90°

得到MBE

二MEC3MBE

・・B£

=EC•AT^AE.=•ZEAC^ZETAB

在Rt&

lZ/l中

・.・AH^AC

・・厶2心="

5=45。

・・・/4号C/4PF-<

MP

即ZEBD=対

・••加△妙二加

又.ZQ4E=45°

••・SADtZEAC-4宁

・・Z£

^8+ZB・4D=45°

即ZTzfZ>

・・・MED丝MED

・・DE二DE

••加"

Zf+fC2

（2）关丢式DE'

=BD-+EC1仍然成立

将A4加沿盲线，仍对折.得心阳，连FE

・•・MFD空5ABD

AFAR.F7）=DR

AD=ZJL4D9MD=ZABD

又•AB=AC.・•AF^AC

•・"

AE=ZFAD+ZDAE二"

AD+45°

£

EAC=ZBAC一ZBAE=90°

-（zLDAE-ZDAB）=45°

4-乙DAB

••・ZFAE=ZEAC

又TAE—AE

..AAFE^AACE

..FE^ECfZAFE=ZACE^45°

厶2=厶80=180°

-厶眈=135°

••・ADFE=ZAFD一ZAFE=135。

一45。

=90°

•在RtAD"

中

DF2+FE2^DE2即QE2hM^+EC2