频谱分析实验报告Word格式.docx
《频谱分析实验报告Word格式.docx》由会员分享,可在线阅读,更多相关《频谱分析实验报告Word格式.docx(13页珍藏版)》请在冰豆网上搜索。
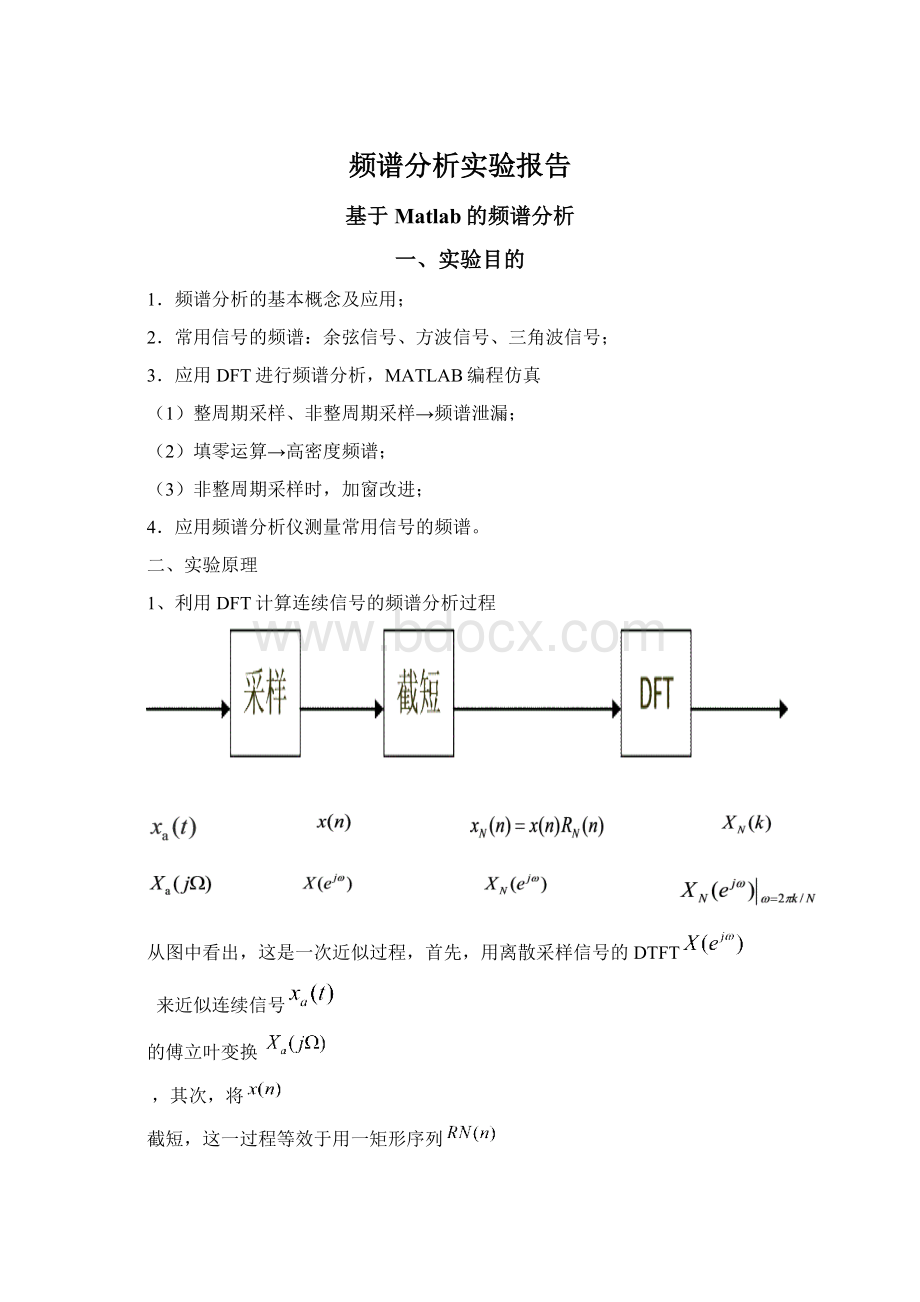
最后,再对截短的信号作DFT
2、频谱分析的近似过程出现问题及解决办法
(1)混叠
①混叠现象
对连续信号x(t)进行数字处理前,要进行采样
采样序列的频谱是连续信号频谱的周期延拓,周期为fs,如采样率过低,不满足采样定理,fs<
2fh,则导致频谱混迭,使一个周期内的谱对原信号谱产生失真,无法恢复原信号,进一步的数字处理失去依据。
另外,干扰信号的频率高于折叠频率
的也会产生频谱混叠。
②对于干扰信号的频率高于
产生频谱混叠的解决办法:
在采样前加一抗混叠滤波器,滤除高于折叠频率
的频率成分。
(2)泄漏
①产生原因
处理实际信号序列x(n)时,一般总要将它截断为一有限长序列,长为N点,相当于乘以一个矩形窗w(n)=RN(n)。
矩形窗函数,其频谱有主瓣,也有许多副瓣,窗口越大,主瓣越窄,当窗口趋于无穷大时,就是一个冲击函数。
我们知道,时域的乘积对应频域的卷积,所以,加窗后的频谱实际是原信号频谱与矩形窗函数频谱的卷积,卷积的结果使频谱延伸到了主瓣以外,且一直延伸到无穷。
当窗口无穷大时,与冲击函数的卷积才是其本身,这时无畸变,否则就有畸变。
例如,信号为
,是一单线谱,但当加窗后,线谱与抽样函数进行卷积,原来在Ω0处的一根谱线变成了以Ω0为中心的,形状为抽样函数的谱线序列,原来在一个周期(Ωs)内只有一个频率上有非零值,而现在一个周期内几乎所有频率上都有非零值,即
的频率成份从Ω0处“泄漏”到其它频率处去了。
考虑各采样频率周期间频谱“泄漏”后的互相串漏,卷积后还有频谱混迭现象产生。
②解决办法:
增加截短的长度N,以减小泄漏。
(3)栅栏效应
①栅栏效应的产生
N点DFT是在频率区间[0,2π]上对信号频谱进行N点等间隔采样,得到的是若干个离散的频谱点X(k),且它们限制在基频的整数倍上,这就好像在栅栏的一边通过缝隙看另一边的景象一样,只能在离散点处看到真实的景象,其余部分频谱成分被遮挡,所以称之为栅栏效应。
②减小栅栏效应方法:
尾部补零,使谱线变密,增加频域采样点数,原来漏掉的某些频谱分量就可能被检测出来。
(4)DFT的分辨率
填补零值可以改变对DTFT的采样密度,人们常常有一种误解,认为补零可以提高DFT的频率分辨率。
事实上我们通常规定DFT的频率分辨率为
,这里的N是指信号x(n)的有效长度,而不是补零的长度。
不同长度的x(n)其DTFT的结果是不同的;
而相同长度的x(n)尽管补零的长度不同其DTFT的结果应是相同的,他们的DFT只是反映了对相同的DTFT采用了不同的采样密度。
参数选择的一般原则:
(1)若已知信号的最高频率
,为防止混叠,选定采样频率
;
(2)根据频率分辩率
,确定所需DFT的长度
(3)
和N确定以后,即可确定相应模拟信号的时间长度
(这里T是采样周期)。
三、实验内容及结果
1、余弦波频谱分析
对余弦函数x(t)=cos(2
*50t)进行频谱分析,采样频率为10000Hz,对其进行整周期采样,非整周期采样,频谱泄露及其改善方法。
其程序代码和运行结果如下。
程序代码:
fs=10000;
t=0:
1/fs:
1.5;
%x
x=cos(2*pi*50*t);
subplot(321),plot(t,x),axis([00.2-1.21.2]);
title('
x(t)=cos(2*pi*50*t)'
);
gridon;
%x(n)
nx=[0:
99];
x0=cos(2*pi*1/50*nx);
subplot(322),stem(nx,x0);
title('
x(n)'
%整周期采样
N1=100;
x1=x0(1:
N1);
X1=fft(x1,N1);
magX1=abs(X1(1:
N1/2+1))*2/N1;
w1=[0:
N1/2]*2*pi/N1;
subplot(323);
stem(w1/pi,magX1);
整周期采样'
%265点DFT,highresolutionspectrum
N2=256;
X=fft(x0,N2);
magX=abs(X(1:
N2/2+1))*2/N2;
w=[0:
N2/2]*2*pi/N2;
subplot(324);
stem(w/pi,magX);
256点DFT,highresolutionspectrum'
%加长矩形窗长度
mx=[0:
149];
xm=cos(2*pi*1/50*mx);
Nm=256;
Y=fft(xm,Nm);
magY=abs(Y(1:
Nm/2+1))*2/Nm;
wm=[0:
Nm/2]*2*pi/Nm;
subplot(325);
stem(wm/pi,magY);
矩形窗加长到150'
%改窗
N=256;
wn=hamming(length(x0));
hn=x0.*wn'
;
H=fft(hn,N);
magH=abs(H(1:
N/2+1))*2/N;
wH=[0:
N/2]*2*pi/N;
subplot(326);
stem(wH/pi,magH);
加hamming窗'
运行结果:
2、方波信号频谱
对方波函数x(t)=square(2
x=square(2*pi*50*t);
x(t)=square(2*pi*50*t)'
x0=square(2*pi*1/50*nx);
xm=square(2*pi*1/50*mx);
3、锯齿波信号频谱
对方波函数x(t)=sawtooth(2
x=sawtooth(2*pi*50*t);
x(t)=sawtooth(2*pi*50*t)'
x0=sawtooth(2*pi*1/50*nx);
xm=sawtooth(2*pi*1/50*mx);
%改窗
4、三角波信号频谱
*50t,0.5)进行频谱分析,采样频率为10000Hz,对其进行整周期采样,非整周期采样,频谱泄露及其改善方法。
x=sawtooth(2*pi*50*t,0.5);
x(t)=sawtooth(2*pi*50*t,0.5)'
x0=sawtooth(2*pi*1/50*nx,0.5);
256点DFT,highresolutionspectrum'
xm=sawtooth(2*pi*1/50*mx,0.5);
5、频率分辨率
频率分辨率是指所用算法能把信号中两个靠得很近的谱峰保持分开的能力。
若两个信号的谱峰靠的很近,很难分开。
为了解决这个问题,可以进行填零运算,但是填零运算产生的是高密度频谱,不能很好的解决。
另一个方法是加长原始信号长度,这样便是产生高分辨率频谱,便可以分开很靠近的两个谱峰。
对函数nx=[0:
x=cos(0.48*pi*nx)+cos(0.52*pi*nx)进行频谱分析,对其进行DTFT,10点DFT,100点DFT,填零运算,高密度频谱和高分辨率频谱。
clear;
clc;
x=cos(0.48*pi*nx)+cos(0.52*pi*nx);
subplot(321);
stem(nx,x);
x(n)=cos(0.48*pi*n)+cos(0.52*pi*n)'
%X(ejw)
200]*pi/200;
X=dtft(x,nx,w);
magX=abs(X);
subplot(322);
plot(w/pi,magX);
X(ejw)'
%10µ
ã
DFT
N1=10;
x1=x(1:
10µ
DFT'
%100µ
DFT£
¬
highresolutionspectrum
N2=100;
X=dft(x,N2);
100µ
highresolutionspectrum'
%Ì
í
90¸
ö
0,100µ
DFT,high-densityspectrum
x2=[x(1:
N1)zeros(1,90)];
n2=0:
N2-1;
stem(n2,x2);
x(n),0<
=n<
=9+90zeros'
X2=fft(x2,N2);
magX2=abs(X2(1:
N2/2+1));
w2=[0:
stem(w2/pi,magX2);
highdensityspectrum'