天津大学应用统计学离线作业及答案Word文档下载推荐.docx
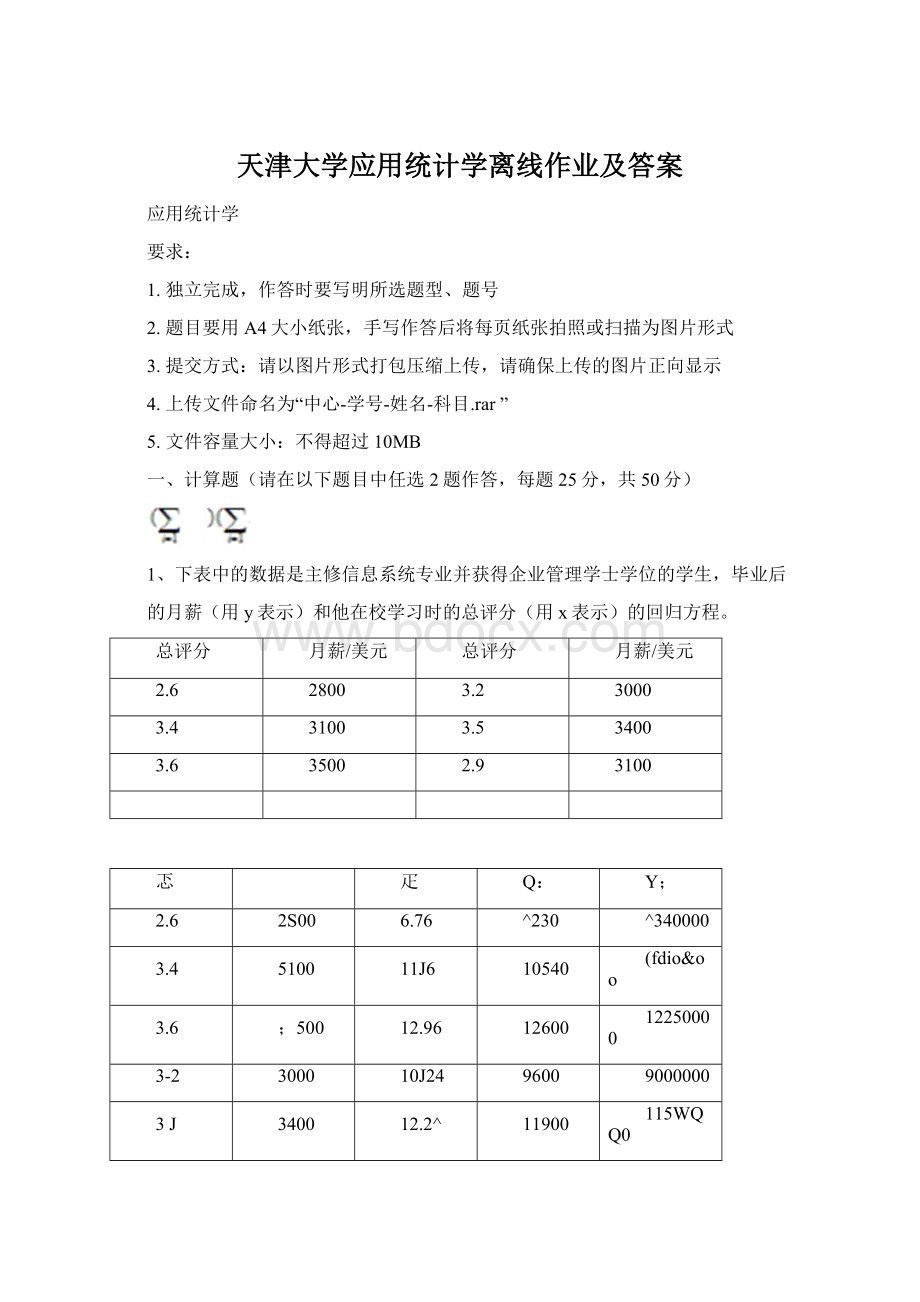
《天津大学应用统计学离线作业及答案Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《天津大学应用统计学离线作业及答案Word文档下载推荐.docx(10页珍藏版)》请在冰豆网上搜索。
500
12.96
12600
12250000
3-2
10J24
9600
9000000
3J
12.2^
11900
115WQQ0
SJL
S950
9610C0D
g
三兀=19-2
歯
yp;
=is<
>
書
=
S2JS
电
yA^.F=6O91Q
=■1
59S7Q000
设F=—r
%=F-内无=LS9D06-35108*19.2&
=12^0_54
于是Ir=t29a34+58108^
2、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上
一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了
1.96
2.2分钟的标准。
2
零假设旳:
n=2.2
设完咸时间的桩准差为叭
即果零槪说立链话,样冷血值应或月姒X'
-心・”2加)
囚沁样本方绘是占昱口的兀侷估计,所以2020.2^2/«
)
那么X的U5%置信区闾(2J-1.9G*0.2/*vrt(45)f2,2+1.MG*0.^/*^4&
))=(2.14(2.26)
内r
因左2孔没苞落在这个蚩信区间内f所以QQ5灵却t水平下更冠绝HQf我:
人为没苞达到?
(Inx)2
2
f(x,)
1
3、设总体X的概率密度函数为
其中为未知参数,Xl,X2,...,Xn是来自X的样本
(1)试求g()31的极大似然估计量?
();
(2)试验证g()是g()的无偏估计量
-I哥』..jX^卫I・口阿—移I』琢兀B
令亦如宀"
酬“”朗$山—陀二。
恥T
解得:
4'
亡眄
厂_JL—I
皿-二屮亠1駐』旳单询函敦,厨既
烈疋的槌大僧懸估计重會f'
{曲总•】
科=
三憧(列)='
工EliUr.^L=J£
|;
lfiT;
-l-5i£
-l=f(p
5
故疸应,是真耳的无偏估计里*
4、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%勺概率满足需要?
诲每月每户至少范备兀
.3^TlO.
当被>
J(ffT,<
TiSS
—10
童表4廿E—g
若供应10M0户,则睿農灌奋104400kg»
5、根据下表中丫与X两个变量的样本数据,建立丫与X的一元线性回归方程。
「\、fj
X'
、
10
15
20
fy
120
8
18
140
3
4
fx
11
28
i殳工为自变星,丫药因叢星,一元统性回归i殳回归方裡拘y上.
5fl=j-^j(=127.1429+1538xl5=l50213
.-回归方程为^150213-153Sx
6、假定某化工原料在处理前和处理后取样得到的含脂率如下表:
处理前
0.140
0.138
0.143
0.142
0.144
0.137
处理后
0.135
0.136
假定处理前后含脂率都服从正态分布,问处理后与处理前含脂率均值有无显著差异。
根耦题中數拒可f聚
=0.141^;
=0.13密£
=0,00235,=0.0027.q=%乂6
田于町=叫=6心山且总休方差未知*所以先用F检验两总体■方差昱否存程差异。
<
L)役瓦;
春£
H】
则F~s(=1.108
S:
由叫=叫=「查F分布得仏(讣7.1乳仏(站)"
14
煽(鸟5)
."
.接受曰「即处理前后两总体方差相同七
设尽乩:
必鼻他
测T=弩总,Sc=心"
用(叫_应
禺匡二i丫W一
r-1.26<
r^(lQ)'
2.2281
「接養朗处理前后含脂率无显着差异。
7、某茶叶制造商声称其生产的一种包装茶叶平均每包重量不低于150克,已知茶叶包装重量服从正态分布,现从一批包装茶叶中随机抽取100包,检验结果如下:
每包重量
包数(包)f
x
xf
x-错误!
未
(X-错误!
(克)
找到引
用
找到引用
源。
)2f
148—149
148.5
1485
-1.8
32.4
149—150
149.5
2990
-0.8
12.8
150—151
50
150.5
7525
0.2
2.0
151—152
151.5
3030
1.2
28.8
合计
100
--
15030
76.0
(1)
计算该样本每包重量的均值和标准差;
(2)以99%勺概率估计该批茶叶平均每包重量的置信区间(10.005(99)~2.626);
(3)在a=0.01的显著性水平上检验该制造商的说法是否可信(to.oi(99)宀2.364)
(4)以95%勺概率对这批包装茶叶达到包重150克的比例作出区间估计(Z0.O25=1.96);
(写出公式、计算过程,标准差及置信上、下保留3位小数)
(3份〉
答:
⑴农中:
组中值工(1分).吕D3QC2分人i}4=76.0<
25>
)
:
、0.6IO2^p^Q.789S(1分)
8—种新型减肥方法自称其参加者在第一个星期平均能减去至少8磅体重.由
40名使用了该种方法的个人组成一个随机样本,其减去的体重的样本均值为7磅,样本标准差为3.2磅•你对该减肥方法的结论是什么?
(a=0.05,卩a/2=1.96,卩a
=1.647)
解:
左硬脸验:
业n>
9Hl;
u<
S
[_Vk<
t-JJS)_X(7-a)_L
纯计星一£
-吉恳—c厂-w所以拒绝和
该咸肥方法没有谨陀宣传的效果°
9、某地区社会商品零售额资料如下:
年份
零售额(亿
元)y
t
t2
ty
1998
21.5
-5
25
-107.5
1999
22.0
44
-3
9
-66
2000
22.5
67.5
-1
-22.5
2001
23.0
16
92
23
2002
24.0
72
2003
25.0
6
36
150
125
138.0
21
91
495
70
24
1)用最小平方法配合直线趋势方程:
2)预测2005年社会商品零售额。
(a,b及零售额均保留三位小数,
苔:
尊有捷法:
⑴,厂1期(1分),Xt-21(1分),
1t-51(2ft),Z1^=495(2
b=(n£
tjLEt込y)fDiL(Z龙)勺=厲汽435-21兀138V[6x
9J-(21)=]
=72/105=0.696想分)
a=Ly/irbl133/6-0.6S6x21/fi=23-0.6BCx3.5=20.599(2
分)
f=a+trt.=20.599+0.«
86t(1分)
(2)2105年t=S亍孟曰Q■匹丹h6S6X6=26.0B7(忆元)(2分)
肯擢法:
(1沱严1M日(1分”It-0(2分,包括2“5厂£
・1,
1t==70(2分),Ety=24(2分)
b=Lty/I-t*=24/70=01343(2分)a=Sy/n=l385/5=23(2分)
g沁34Jt(1和
(2)2005年t=9i^,^=23+0.343X'
9^26.0S7t亿元)(2分)
10、某商业企业商品销售额1月、2月、3月分别为216,156,180.4万元,月初职工人数1月、2月、3月、4月分别为80,80,76,88人,试计算该企业1月、2月、3月各月平均每人商品销售额和第一季度平均每月人均销售额。
(写出计算过程,结果精确到0.0001万元人)
1月平均每人销售^=216/[(80^60)72)=2.70万元从(1分)
2月平均每人销售§
j=156/[(80+73)721=2.0万元从(吩】
3月平均每人销售额=190.4/[(76^8)/2]=2.20万元/人〔i分〉
第—季度平均捕月人均销售锁
=[(216+15^+180.4)/3]/[(00/2-^00+76486/2)/3]
=553.4/240=184.13/80=2.3017万元丿人<
驸)
二、简答题(请在以下题目中任选2题作答,每题25分,共50分)
1.区间估计与点估计的结果有何不同?
点估计是使用估计量的单一值作为总体参数的估计值;
区间估计是指定估计
量的一个取值范围都为总体参数的估计。
2.解释抽样推断的含义。
简单说,就是用样本中的信息来推断总体的信息。
总体的信息通常无法获得或者没有必要获得,这时我们就通过抽取总体中的一部分单位进行调查,利用
调查的结果来推断总体的数量特征。
3.统计调查的方法有那几种?
三种主要调查方式:
普查,抽样调查,统计报表。
实际中有时也用到重点调查和典型调查。
4.时期数列与时点数列有哪些不同的特点?
区;
(1)时期指标的数值是连续登记的「而时点指标的戴值是在某个时间点上问断计数取得的;
(2)时期指标的数值具有鬆仙性时点揩标的数值不具肓罠扣性;
〔时期斶数佰旳大丿」百所登运时期辰短有宜接黃系■对原指标数值大李与肝登记时期的谊短没有关爲
5.为什么要计算离散系数?
离散系数是指一组数据的标准差与其相应得均值之比,也称为变异系数。
对于平均水平不同或计量单位不同的不同组别的变量值,是不能用方差和标准差
比较离散程度的。
为消除变量值水平高低和计量单位不同对离散程度测度值的影响,需要计算离散系数。
离散系数的作用主要是用于比较不同总体或样本数据的离散程度。
离散系数大的说明数据的离散程度也就大,离散系数小的说明数据的离散程度也就小。
6.简述普查和抽样调查的特点。
普查是指为某一特定目的而专门组织的全面调查,它具有以下几个特点:
(1)普查通常具有周期性。
(2)普查一般需要规定统一的标准调查时间,以
避免调查数据的重复或遗漏,保证普查结果的准确性。
(3)普查的数据一般
比较准确,规划程度也较高。
(4)普查的使用范围比较窄。
抽样调查指从调
查对象的总体中随机抽取一部分单位作为样本进行调查,并根据样本调查结果来
推断总体数量特征的一种数据收集方法。
它具有以下几个特点:
(1)经济性。
这是抽样调查最显著的一个特点。
(2)时效性强。
抽样调查可以迅速、及时
地获得所需要的信息。
(3)适应面广。
它适用于对各个领域、各种问题的调查。
(4)准确性高。
7.简述算术平均数、几何平均数、调和平均数的适用范围。
几何平均数主要适用于比率的平均。
一般地说,如果待平均的变量x与另外两个变量f和m有fx=m的关系时,若取f为权数,应当采用算术平均方法;
若取m为权数,应当采用调和平均方法。
8.假设检验的基本依据是什么?
根据所获得的样本,运用统计分析方法对总体的某种假设作出拒绝或接受的判
断。
大数定理和实际推断原理:
小概率事件在一次抽样中是不可能发生的。
9.表示数据分散程度的特征数有那几种?
全距(又称极差),方差和标准差,交替标志的平均数和标准差,变异系
数,标准分数。
10.回归分析与相关分析的区别是什么?
1、在回归分析中,y被称为因变量,处在被解释的特殊地位,而在相关分析中,x与
y处于平等的地位,即研究x与y的密切程度和研究y与x的密切程度是一致的;
2、相关分析中,x与y都是随机变量,而在回归分析中,y是随机变量,x可以是随机变量,
也可以是非随机的,通常在回归模型中,总是假定x是非随机的;
3、相关分析的研究主要是两个变量之间的密切程度,而回归分析不仅可以揭示x对y的影响大小,还可以由回归方程进行数量上的预测和控制。
11.在统计假设检验中,如果轻易拒绝了原假设会造成严重后果时,应取显著性水平较大还是较小,为什么?
取显著性水平较小,因为如果轻易拒绝了原假设会造成严重后果,那就说明在统计假设检验中,拒绝原假设的概率要小,而假设检验中拒绝原假设的概率正是事先选定的显著性水平a
12.加权算术平均数受哪几个因素的影响?
若报告期与基期相比各组平均数没变,则总平均数的变动情况可能会怎样?
请说明原因。
13.解释相关关系的含义,说明相关关系的特点
变量之间存在的不确定的数量关系为相关关系。
相关关系的特点:
一个
变量的取值不能由另一个变量唯一确定,当变量x取某个值时,变量y的取值可能有几个;
变量之间的相关关系不能用函数关系进行描述,但也不是无任何规律可循。
通常对大量数据的观察与研究,可以发现变量之间存在一定的客观规律。
14.为什么对总体均值进行估计时,样本容量越大,估计越精确?
因为总体是所要认识的研究对象的全体,它是具有某种共同性质或特征的许多单位的集合体•总体的单位数通常用N来表示,N总是很大的数.样本是总体
的一部分,它是从总体中随机抽取出来、代表总体的那部分单位的集合体.样本的单位数称为样本容量,通常用n表示。
样本容量n越大,就越接近总体单位数N,样本均值就越接近总体均值,对总体均值进行估计时,估计越精确。