北师大初一下数学《整式的乘除》和《平行线与相交线》第一二单元综合练习二含答案Word文档格式.docx
《北师大初一下数学《整式的乘除》和《平行线与相交线》第一二单元综合练习二含答案Word文档格式.docx》由会员分享,可在线阅读,更多相关《北师大初一下数学《整式的乘除》和《平行线与相交线》第一二单元综合练习二含答案Word文档格式.docx(32页珍藏版)》请在冰豆网上搜索。
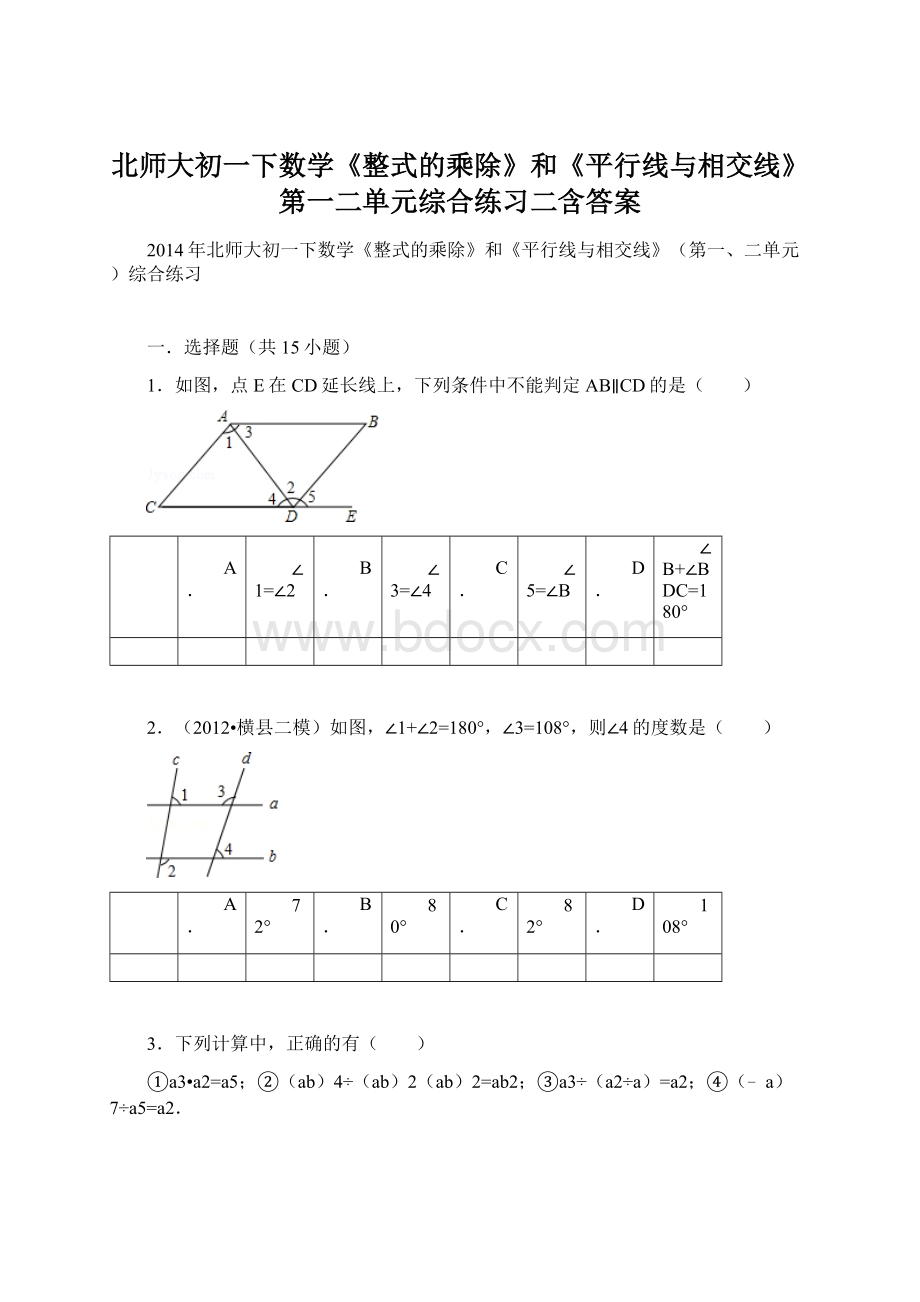
5
3;
5;
3
6;
12
5.如果(x﹣2)(x+3)=x2+px+q,那么p、q的值为( )
p=5,q=6
p=﹣1,q=6
p=1,q=﹣6
p=5,q=﹣6
6.已知3m=4,3n=5,3m﹣2n+1的值为( )
7.(2008•宁德)如图,已知AB∥CD,∠A=70°
,则∠1度数是( )
70°
100°
110°
130°
8.(x2)3的计算结果为( )
x5
x6
3x2
x3
9.﹣5x•(2x2﹣x+3)的计算结果为( )
﹣10x3+5x2﹣15x
﹣10x3﹣5x2+15x
10x3﹣5x2﹣15x
﹣10x3+5x2﹣3
10.如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°
;
(2)∠1=∠2;
(3)∠3=∠4;
(4)∠B=∠5.
1
2
4
11.如图,直线a,b被c所截,a∥b,若∠1=30°
,则∠2的大小为( )
150°
135°
120°
105°
12.如图,已知直线l1∥l2,∠1=30°
,∠2=80°
,那么∠3的大小为( )
90°
13.若am=2,an=3,则am+n等于( )
6
8
9
14.如图,下列说法错误的是( )
∠A与∠B是同旁内角
∠3与∠1是同旁内角
∠2与∠3是内错角
∠1与∠2是同位角
15.如图:
BO、CO是∠ABC,∠ACB的两条角平分线,∠A=100°
,则∠BOC的度数为( )
140°
二.填空题(共6小题)
16.若(ambn)2=a8b6,则m= _________ ,n= _________ .
17.若x2+px+8=(x﹣2)(x﹣q),则p= _________ ,q= _________ .
18.已知2m+3n=3,则4m•8n的值为 _________ .
19.若am=3,an=2,则am+n= _________ .
20.已知am=2,an=3,求am+n= _________ ,am﹣n= _________ .
21.如图,AB∥DE,∠E=65°
,则∠B+∠C= _________ .
三.解答题(共9小题)
22.计算
(1)((π﹣2)0﹣|﹣5|+(﹣1)2012
(2)﹣(2x)2•3xy2(3)0.125100×
8101
(4)(a+4)×
(a﹣4)﹣(a﹣1)
23.计算:
(1)(2xy2)3﹣(5xy2)•(﹣xy2)2
(2)
24.如图,已知AB∥CD,∠1=40°
,∠2=70°
,
求出∠3,∠4的度数.
25.已知:
如图,AB∥CD,求∠A+∠E+∠C的度数.
26.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°
,求∠AOC和∠COB的度数.
27.已知△ABC中,∠B=70°
,CD平分∠ACB,∠2=∠3,求∠1的度数.
28.如图,已知AD∥BE,∠CDE=∠C,试说明∠A=∠E的理由.
29.已知:
如图,∠A=∠F,∠C=∠D.
求证:
BD∥CE.
30.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
AD∥BC.
参考答案与试题解析
考点:
平行线的判定.1863781
分析:
根据平行线的判定方法直接判定.
解答:
解:
选项B中,∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),所以正确;
选项C中,∵∠5=∠B,∴AB∥CD(内错角相等,两直线平行),所以正确;
选项D中,∵∠B+∠BDC=180°
,∴AB∥CD(同旁内角互补,两直线平行),所以正确;
而选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,故A错误.
故选A.
点评:
正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
平行线的判定与性质.1863781
专题:
计算题.
由邻补角定义得到∠2与∠5互补,再由∠1与∠2互补,利用同角的补角相等得到∠1=∠5,利用同位角相等两直线平行得到a与b平行,利用两直线平行同旁内角互补得到∠6与∠4互补,而∠3与∠6对顶角相等,由∠3的度数求出∠6的度数,进而求出∠4的度数.
∵∠1+∠2=180°
,∠2+∠5=180°
∴∠1=∠5,
∴a∥b,
∴∠4+∠6=180°
∴∠4=72°
.
故选A
此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
幂的乘方与积的乘方;
同底数幂的乘法;
同底数幂的除法.1863781
①利用同底数幂的乘法求解即可;
②首先利用同底数幂的除法计算出(ab)4÷
(ab)2的结果,再利用同底数幂的乘法计算即可;
③先算括号里面的,再算括号外面的即可求得答案;
④注意负数的奇次方是负数,再利用同底数幂的除法计算即可.
∵①a3•a2=a5;
(ab)2(ab)2,
=(ab)2•(ab)2,
=(ab)4,
=a4b4;
a),
=a3÷
a,
=a2;
a5,
=﹣a7÷
=﹣a2.
∴正确的有①③.
故选B.
本题考查了同底数幂的乘法与除法,幂的乘方,积的乘方以及简单的混合运算.理清指数的变化是解题的关键
幂的乘方与积的乘方.1863781
根据积的乘方法则展开得出a3mb3n=a9b15,推出3m=9,3n=15,求出m、n即可.
∵(ambn)3=a9b15,
∴a3mb3n=a9b15,
∴3m=9,3n=15,
∴m=3,n=5,
本题考查了积的乘方的运用,关键是检查学生能否正确运用法则进行计算,题目比较好,但是一道比较容易出错的题目.
多项式乘多项式.1863781
先根据多项式乘以多项式的法则,将(x﹣2)(x+3)展开,再根据两个多项式相等的条件即可确定p、q的值.
∵(x﹣2)(x+3)=x2+x﹣6,
又∵(x﹣2)(x+3)=x2+px+q,
∴x2+px+q=x2+x﹣6,
∴p=1,q=﹣6.
故选C.
本题主要考查多项式乘以多项式的法则及两个多项式相等的条件.多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.两个多项式相等时,它们同类项的系数对应相等.
同底数幂的除法;
先根据同底数幂的乘法及除法,幂的乘方与积的乘方法则把原式化为3m÷
(3n)2×
3的形式,再把3m=4,3n=5代入进行计算即可.
原式=3m÷
=4÷
52×
=
×
本题考查的是同底数幂的乘法及除法,幂的乘方与积的乘方法则,能逆用此法则把原式化为3m÷
3的形式是解答此题的关键.
平行线的性质;
对顶角、邻补角.1863781
两条直线平行,内错角相等,然后根据邻补角的概念即可解答.
∵AB∥CD,∠A=70°
∴∠2=70°
(两直线平行,内错角相等),
再根据平角的定义,得
∠1=180°
﹣70°
=110°
注意平行线的性质的运用,此类题方法要灵活.也可以求得∠A的同旁内角,再根据对顶角相等,进行求解.
根据幂的乘方,底数不变指数相乘,计算后直接选取答案即可.
(x2)3=x2×
3=x6.
本题考查幂的乘方的性质,熟练掌握性质是解题的关键.
单项式乘多项式.1863781
首先利用分配律把5x乘到括号内,然后依据去括号法则化简即可.
原式=﹣(10x3﹣5x2+15x)=﹣10x3+5x2﹣15x.
本题考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.
在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
(1)利用同旁内角互补判定两直线平行,正确;
(2)利用内错角相等判定两直线平行.∵∠1=∠2,∴AD∥BC,而不能判定AB∥CD,故错误;
(3)利用内错角相等判定两直线平行,正确;
(4)利用同位角相等判定两直线平行,正确.
正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
平行线的性质.1863781
求出∠3,根据平行线性质得出∠2+∠3=180°
,代入求出即可.
∵∠1=30°
∴∠3=∠1=30°
∵a∥b,
∴∠2+∠3=180°
∴∠2=150°
本题考查了平行线性质和对顶角相等的应用,主要考查学生的推理能力.
根据两直线平行,内错角相等求出∠4,然后利用三角形内角和定理列式计算即可得解.
∵l1∥l2,
∴∠4=∠2=80°
根据三角形内角和定理,∠3=180°
﹣∠1﹣∠4=180°
﹣30°
﹣80°
=70°
本题考查了平行线的性质,三角形内角和定理,准确识图是解题的关键.
同底数幂的乘法.1863781
根据am•an=am+n,将am=2,an=3,代入即可.
∵am•an=am+n,am=2,an=3,
∴am+n=2×
3=6.
此题考查了同底数幂的乘法运算,属于基础题,解答本题的关键是掌握同底数幂的乘法法则,难度一般.
同位角、内错角、同旁内角.1863781
根据内错角:
两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
同旁内角:
两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角可得答案.
A、∠A与∠B是同旁内角,说法正确;
B、∠3与∠1是同旁内角,说法正确;
C、∠2与∠3是内错角,说法正确;
D、∠1与∠2是邻补角,原题说法错误,
故选:
此题主要考查了三线八角,在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
角平分线的定义;
三角形内角和定理.1863781
△ABC中,已知∠A即可得到∠ABC与∠ACB的和,而BO、CO是∠ABC,∠ACB的两条角平分线,即可求得∠OBC与∠OCB的度数,根据三角形的内角和定理即可求解.
△ABC中,∠ABC+∠ACB=180°
﹣∠A=180°
﹣100°
=80°
∵BO、CO是∠ABC,∠ACB的两条角平分线.
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=40°
在△OBC中,∠BOC=180°
﹣(∠OBC+∠OCB)=140°
故选D.
本题主要考查了三角形的内角和定理,以及三角形的角平分线的定义.
16.若(ambn)2=a8b6,则m= 4 ,n= 3 .
根据积的乘方法则展开得出a2mb2n=a8b6,推出2m=8,2n=6,求出m、n即可.
∵(ambn)2=a8b6,
∴a2mb2n=a8b6,
∴2m=8,2n=6,
∴m=4,n=3.
故答案为:
4,3.
17.若x2+px+8=(x﹣2)(x﹣q),则p= ﹣6 ,q= 4 .
因式分解-十字相乘法等.1863781
已知等式右边利用多项式乘以多项式法则计算,再利用多项式相等的条件即可确定出p与q的值.
x2+px+8=(x﹣2)(x﹣q)=x2﹣(q+2)x+2q,
可得p=﹣q﹣2,2q=8,
解得:
p=﹣6,q=4.
﹣6;
此题考查了因式分解﹣十字相乘法,熟练掌握十字相乘法是解本题的关键.
18.已知2m+3n=3,则4m•8n的值为 8 .
把4m•8n转化为同底数相乘的形式,根据同底数幂的乘法的性质来求值.
4m•8n=
(2)2m×
(2)3n=
(2)2m+3n,
∵2m+3n=3,
∴
(2)2m+3n=
(2)3=8.
故答案为8.
本题考查了同底数幂的乘法,属于基础题,较为简单.
19.若am=3,an=2,则am+n= 6 .
先根据同底数幂的乘法法则把代数式化为已知的形式,再把已知代入求解即可.
∵am•an=am+n,
∴am+n=am•an=3×
2=6.
解答此题的关键是熟知同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加,即am•an=am+n.
20.已知am=2,an=3,求am+n= 6 ,am﹣n=
.
根据同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加可知:
指数相加可以化为同底数幂的乘法;
根据同底数幂的除法法则:
底数不变,指数相减可知:
指数相减,可以化为同底数幂的除法.
am+n=am•an=2×
3=6;
am﹣n=am÷
an=2÷
3=
此题主要考查了同底数幂的乘、除法,关键是熟练掌握计算法则,并能进行逆运用.
,则∠B+∠C= 65°
三角形的外角性质.1863781
根据两直线平行,内错角相等,求出关于△BCF的外角,再根据外角的性质求解.
∵AB∥DE,∠E=65°
∴∠E=∠BFE=65°
∵∠BFE=∠B+∠C,
∴∠B+∠C=65°
本题比较简单,考查的是平行线的性质及三角形内角与外角的关系.
整式的混合运算;
零指数幂.1863781
(1)原式第一项利用零指数幂法则计算,第二项利用负数的绝对值等于它的相反数计算,最后一项利用﹣1的偶次幂为1计算即可得到结果;
(2)原式先利用积的乘方运算法则计算,再利用单项式乘单项式法则计算即可得到结果;
(3)原式利用积的乘方运算法则变形计算即可得到结果;
(4)原式第一项利用平方差公式化简,去括号合并即可得到结果.
(1)原式=1﹣5+1=﹣3;
(2)原式=﹣4x2•3xy2=﹣12x3y2;
(3)原式=(0.125×
8)100×
8=8;
(4)原式=a2﹣16﹣a+1=a2﹣a﹣15.
此题考查了整式的混合运算,涉及的知识有:
完全平方公式,平方差公式,积的乘方与幂的乘方,去括号法则,以及合并同类项法则,熟练掌握公式及法则是解本题的关键.
负整数指数幂;
专题