拉格朗日插值实验报告文档格式.docx
《拉格朗日插值实验报告文档格式.docx》由会员分享,可在线阅读,更多相关《拉格朗日插值实验报告文档格式.docx(12页珍藏版)》请在冰豆网上搜索。
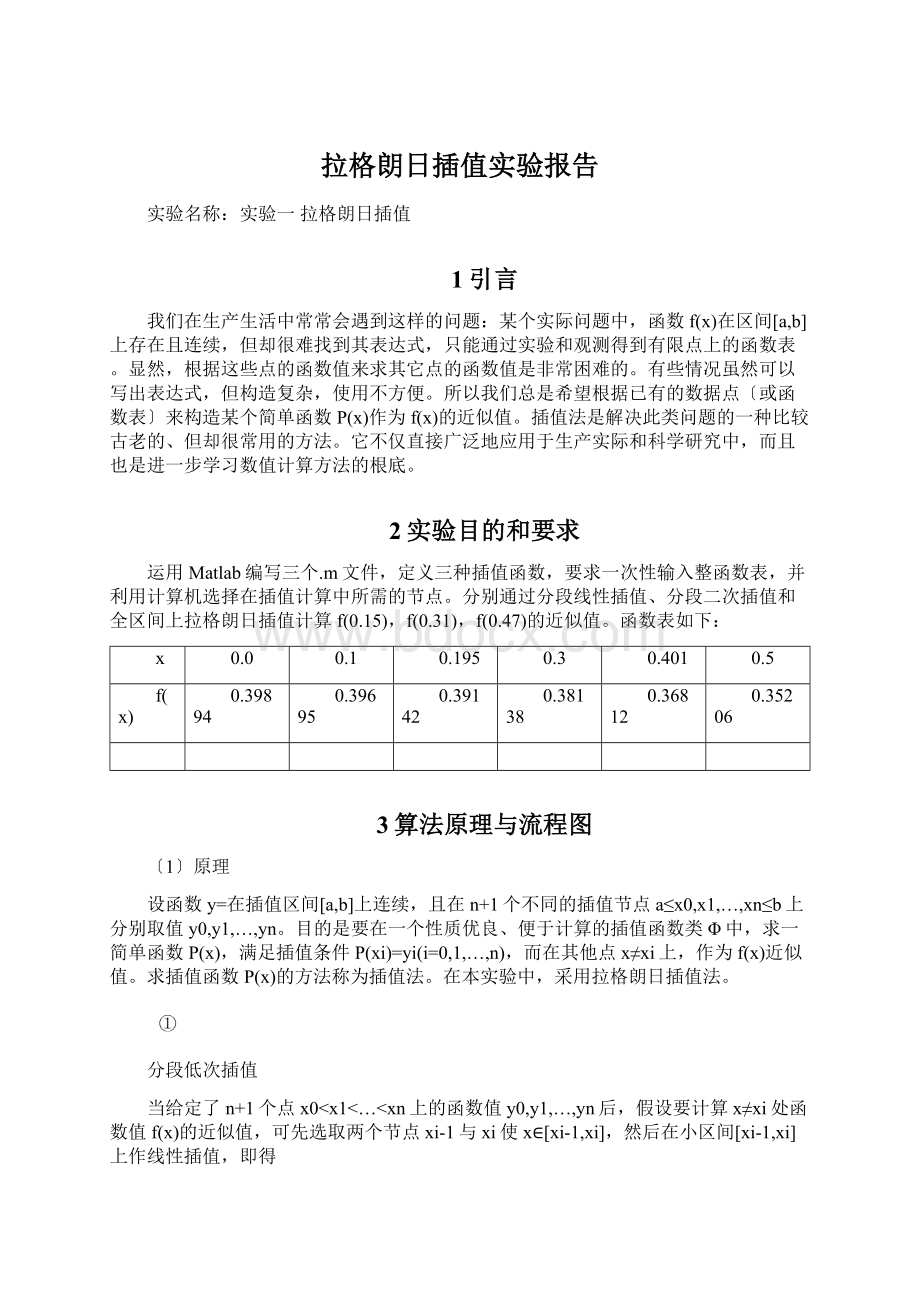
0.401
0.5
f(x)
0.39894
0.39695
0.39142
0.38138
0.36812
0.35206
3算法原理与流程图
〔1〕原理
设函数y=在插值区间[a,b]上连续,且在n+1个不同的插值节点a≤x0,x1,…,xn≤b上分别取值y0,y1,…,yn。
目的是要在一个性质优良、便于计算的插值函数类Φ中,求一简单函数P(x),满足插值条件P(xi)=yi(i=0,1,…,n),而在其他点x≠xi上,作为f(x)近似值。
求插值函数P(x)的方法称为插值法。
在本实验中,采用拉格朗日插值法。
分段低次插值
当给定了n+1个点x0<
x1<
…<
xn上的函数值y0,y1,…,yn后,假设要计算x≠xi处函数值f(x)的近似值,可先选取两个节点xi-1与xi使x∈[xi-1,xi],然后在小区间[xi-1,xi]上作线性插值,即得
这种分段低次插值叫分段线性插值,又称折线插值。
类似地,我们可以选取距离x最近的三个节点xi-1,xi与xi+1,然后进展二次插值,即得
这种分段低次插值叫分段二次插值,又称分段抛物线插值。
全区间上拉格朗日插值
对节点xi(i=0,1,…,n)中任一点xk(0≤k≤n),作一n次多项式lk(x),使它在该点上的取值为1,在其余点xi(i=0,1,…,k-1,k+1,…,n)上取值为零。
对应于每一节点xk(k=0,1,…,n),都能写出一个满足此条件的多项式,这样写出了n+1个多项式l0(x),l1(x),…,ln(x),其中
;
由条件
可得
于是我们可以得出如下的拉格朗日n次插值多项式〔对于全区间上的插值,n取函数表的长度〕
(2)流程图
分段线性插值分段二次插值全区间拉格朗日插值
4程序代码及注释
1、分段线性插值
%分段线性插值
functiony=piece_linear(x0,y0,x)
%x0,y0为点,x为待求点
n=length(x0);
p=length(y0);
m=length(x);
%n,p,m分别为x0,y0,x长度
ifn~=p
fprintf('
Error!
Pleaseinputagain!
\n'
);
%x0和y0长度不等时,报错
else
fori=1:
m
z=x(i);
sum=0.0;
l=0;
%给l赋初值,根据x的值确定l
ifz<
x0
(1)|z>
x0(n)
x(%d)isoutofrange!
i);
break;
end
%当插值点超出围时,报错
forj=2:
n
x0(j)
l=j;
ifl~=0
%一旦l有非零值,那么终止循环,选出适宜的l
fork=l-1:
l
a=1.0;
fors=l-1:
ifs~=k
a=a*(z-x0(s))/(x0(k)-x0(s));
sum=sum+y0(k)*a;
y(i)=sum;
y(%d)=%f\nx1=%.3fy1=%.5f,x2=%.3fy2=%.5f\n\n'
i,y(i),x0(l-1),y0(l-1),x0(l),y0(l));
%输出插值结果和所需节点
2、分段二次插值
%分段二次插值
functiony=piece_square(x0,y0,x)
forj=1:
n-2
p=0.5*(x0(j)+x0(j+1));
p
ifl==0
l=n-1;
%输入正确时,假设l还等于零,l=n-1
l+1
fprintf('
y(%d)=%f\nx1=%.3fy1=%.5f\nx2=%.3fy2=%.5f\nx3=%.3fy3=%.5f\n\n'
i,y(i),x0(l-1),y0(l-1),x0(l),y0(l),x0(l+1),y0(l+1));
%输出插值结果与所需节点
3、拉格朗日全区间插值
%拉格朗日全区间插值
functiony=lagrange(x0,y0,x)
%x0,y0为点,x为待求点
s=0.0;
fork=1:
p=1.0;
ifj~=k
p=p*(z-x0(j))/(x0(k)-x0(j));
s=p*y0(k)+s;
y(i)=s;
y(%d)=%.5f\n'
i,y(i));
%输出插值结果
5算例分析
1、测试例如
>
x=[1234];
y=[234];
y2=lagrange(x,y,x0)
y=[2345];
x0=[0.55.5];
x
(1)isoutofrange!
x0=[1.55.5];
y
(1)=2.50000
x
(2)isoutofrange!
y2=
2.500000000000000
2、首先输入函数变及待求点
x=[0.00.10.1950.30.4010.5];
y=[0.398940.396950.391420.381380.368120.35206];
x0=[0.150.310.47];
注:
保证在matlab工作目录中有三个.m文件
3、分段线性插值
y0=piece_linear(x,y,x0)
y
(1)=0.394039
x1=0.100y1=0.39695,x2=0.195y2=0.39142
y
(2)=0.380067
x1=0.300y1=0.38138,x2=0.401y2=0.36812
y(3)=0.356927
x1=0.401y1=0.36812,x2=0.500y2=0.35206
y0=
0.3940394736842110.3800671287128710.356926666666667
4、分段二次插值
y1=piece_square(x,y,x0)
y
(1)=0.394460
x1=0.100y1=0.39695
x2=0.195y2=0.39142
x3=0.300y3=0.38138
y
(2)=0.380225
x1=0.195y1=0.39142
x2=0.300y2=0.38138
x3=0.401y3=0.36812
y(3)=0.357247
x1=0.300y1=0.38138
x2=0.401y2=0.36812
x3=0.500y3=0.35206
y1=
0.3944603195488720.3802246915953730.357246844884488
5、全区间拉格朗日插值
y
(1)=0.39447
y
(2)=0.38022
y(3)=0.35722
0.3944728038780610.3802190624547320.357222112339485
6讨论与结论
1、使用tic,toc函数计算以下四种方法计算上述问题所运行的时间
Function
lagrange(x0,y0,x)
piece_linear(x0,y0,x)
piece_square(x0,y0,x)
运行时间(s)
0.000272
0.000375
从三次实验结果可知,三个程序的运行时间都很短。
2、程序优化
由分段线性插值和分段二次插值的原理,x取值在函数表围时,插值结果有意义,而当x取值在函数表围以外,利用分段线性插值公式仍可以进展运算并得到一个值,但其结果不准确;
分段二次插值那么无法找到三个适宜的点以求插值,不予以输出结果;
假设输入的函数表x与y的长度不相等,那么无法插值。
所以参加以下判断以提高插值的准确性
3、作图比较
上图为三种方法的插值曲线,其中x取0到0.5,步长为0.001,由图可得,三种曲线非常接近,这说明我们用拉格朗日插值计算所给点函数值的近似值时,引起的误差还是比较小的。
参考文献
[1]易大义,云宝,有法.计算方法(第2版),大学.p.29-53.
[2]琨高思超毕靖编著MATLAB2021从入门到精通电子工业