高代竞赛辅导第7章线性空间.docx
《高代竞赛辅导第7章线性空间.docx》由会员分享,可在线阅读,更多相关《高代竞赛辅导第7章线性空间.docx(15页珍藏版)》请在冰豆网上搜索。
高代竞赛辅导第7章线性空间
七线性空间
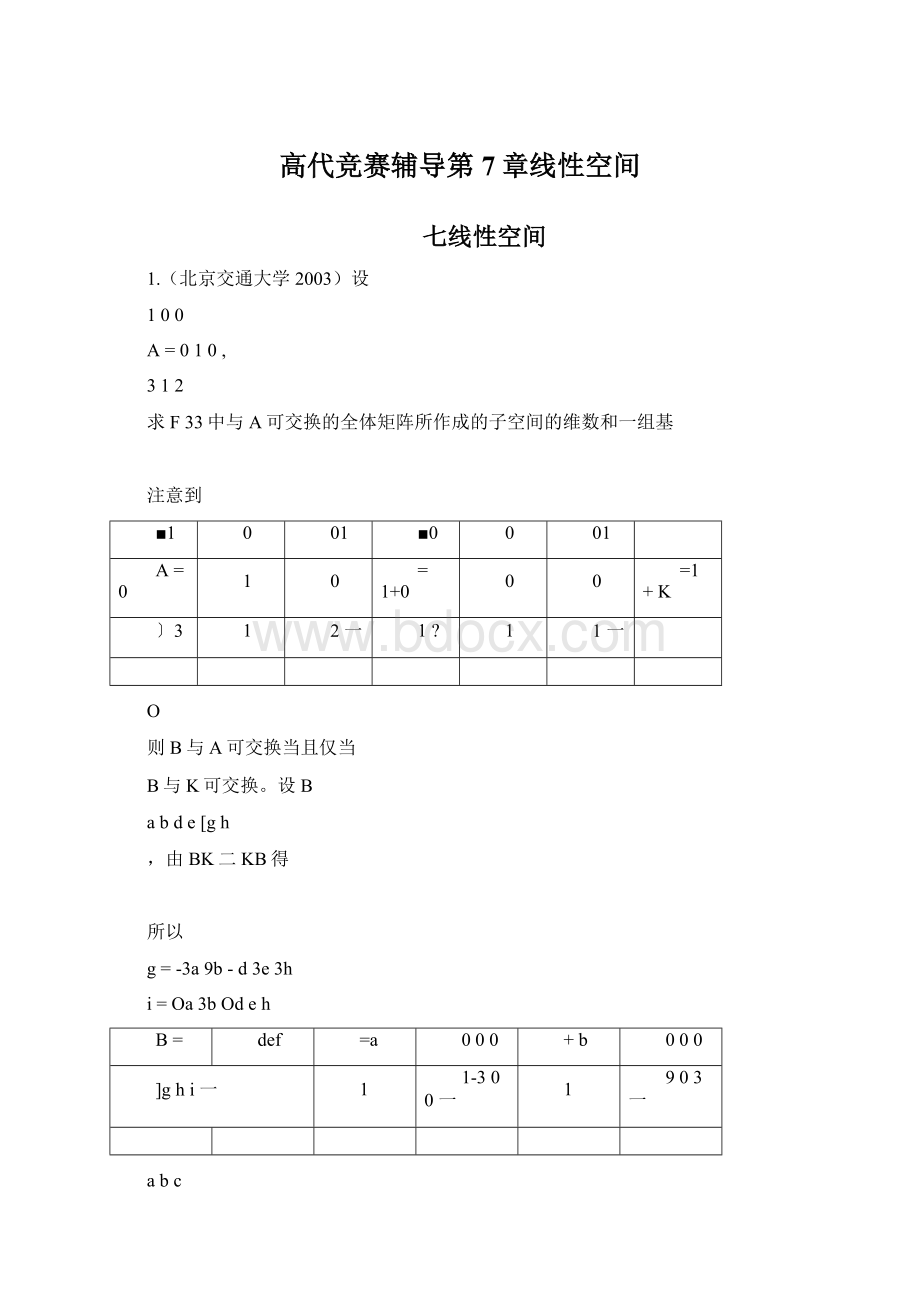
1.(北京交通大学2003)设
100
A=010,
312
求F33中与A可交换的全体矩阵所作成的子空间的维数和一组基
注意到
■1
0
01
■0
0
01
A=0
1
0
=1+0
0
0
=1+K
〕3
1
2一
1?
1
1一
O
则B与A可交换当且仅当
B与K可交换。
设B
abde[gh
,由BK二KB得
所以
g=-3a9b-d3e3h
i=Oa3bOdeh
B=
def
=a
000
+b
000
]ghi一
1
1-300一
1
903一
abc
100010
0
+d1
■-1
00000000
00+e010+h000
00_卫01一11一
因此与A可交换的全体矩阵所作成的子空间的维数为5,一组基为
100010000000000
IIIIIIIdnIInnI
000,000,100,|010,|000。
-300一.903_「100_h01_〔311_
2.(西安交通大学2004)设
「2、
■Z1、
3、
z
1
-
-1
3
5
j
-1,
C(2=
1,
a3=—
3,i
丄4——
5R5
-1
1
―
3
—
5
J」
<2丿
4>
7
■」
记WK〉1,〉2,〉3“4•,求W-的基和维数。
解分析:
令A=(:
•i,2,〉3,〉4),贝VxW_=X_W=
于是只需求线性方程组ATx=0,它的基础解系就是W-的一组基
f
1?
1
0
0
0
——
'2
1
-1
-1
1
3
T
1
—1
1
1
—2
5
A=
严
0
1
_1
-1
3
3
-3
-3
4
1
3
|
<4
5
-5
-5
7
丿
0
0
0
0
0
1°
0
0
0
0」
得ATX=0的一个基础解系
广0、
•s
5、
1
1
-5
1
―
0
0
0
1
0
<3」
它就是W-的一组基,且W-的维数等于3.
■a
0
b
1
「x0
N、
1
3.(天津大学2004)
已知W1=」
c
0
b
|a,b,c,dwR
'W2=t
0z
0
|x,y,z^R卜
-
<0
c
d丿
-
I
0
0丿
-
求W1+W2及W1aW2
的基和维数
。
'a0b
解由c0b=aEn+b(Ei3+E23)+c(E2i+E32)+dE33知dimV^4
0cd」
=xE11>
yEi3zE22知dimy=3。
那么有
■'a
0
b、
zx
0
yA
c
0
b
+
0
z
0
1°
c
d」
1°
0
°」
二(ax)Eii(by)Ei3
bE23(CZ)E2icE32dE33
c,z任意,
贝yC-z任意。
b.d.a-x.b-y任意,
得dim
E11•WiW2,所以可取Eh
2阶矩阵构成的线性空间,
Eii.Ei3.E23.E2i.E32.E33,是WiW2的一组基。
于是
dim(WiW2)=dimWidimW^dim(WiW2)=1,且显然
为W.W2的一组基。
4.(上海交通大学2003)以F22表示数域F上全体
a1.a2.a3.a4为两两互异的数且它们的和不等于零。
证明
ri
ai
、
ri
a2
、
5
a3
X
ri
a4
Ai=
2
4
.A2—
2
4
.A3—
2
4
.A4=
2
4
lai
ai
J
a2
丿
la3
a3
)
la4
a
4
是F22的一组基。
证明
2戌
dimF=4
Eii.Ei2.E2i.E22^是F
22的一组基,
(A1,A2,A3,A4)
—(Eii.Ei2.E2i.E22)
a2
2
a2
4
a2
a3
2
a3
4
a3
a4
2
a4
4
a4J
i
i
i
i
i
i
i
i
i
ai
a2
a3
a4
a
ai
a2
a3
a4
.D=
2
2
2
2
2
2
2
2
2
ai
a2
a3
a4
a5
ai
a2
a3
a4
3
3
3
3
3
4
4
4
4
ai
a2
a3
a4
a5
ai
a2
a3
a4
4
4
4
4
4
ai
a2
a3
a4
a5
5
一ai]心5
a5
-a2
=a5
-a3]i.a5-a4
=''ai-aj
i」:
i:
兰
a「aj
1_j心
而d是D的M45
--A45
二a5的系数,
d=-a1a
2•a3•a4…ai
iJ_4
_aj。
由已知条件ai,a2,a3,a4为两两互异的数且它们的和不等于零,所以d=0,于是
证明令J=
<0
i0…
0、
0
0i…
0
+++
9
*
0
…"•0
i
0…0
0丿
,注意到
J2,J3/,JnJ的形式及I,那么有
Ai,A2,A3,A4是F22的一组基。
a3
=aiIa2Ja3anJ。
=aila2Ja3J2一八丁anJn',B=bilb2Jb3J2丁一一bnJn_i
贝廿AB=(aibjl(a2-b2)J(a3-bs)J2(a.bn)Jn‘U,
kA=(kai)l(ka2)J(ka3)J2(kan)JnJU,
所以U是Mn(F)的一个子空间。
注意到I,J,J2^,Jn-i线性无关且U中的每个矩阵
都可以表示成l,J,J2,Jn」的线性组合,所以l,J,J2,…,Jn‘是U的一组基,dimU=n。
6.(北京师范大学2006)设V是数域F上的一个n维线性空间,"V是V的两个子空间,且dimy=dimV2=r。
证明:
存在V的一个子空间W,使得V=Vi二W二V2二W.
证明若r二n,则Vi二V2=V,取W=0,结论成立。
若r”n,则存在「Vi,「V2。
分别取Vi,V2的一组基—r,「…",贝Vi
:
r,1线性无关,
不能由:
r,…,:
r线性表出,也不能由:
1,…,:
r线性表出,所以
订…,>,i线性无关,得两个r1维子空间
Vj=:
:
:
〉r,…,〉r,1=Vj二:
:
:
1-,72二「「■,:
!
•,1=V?
二:
:
:
1。
如果r•仁n,则取1.,结论成立。
如果r・仁:
n,则继续上面过程,存在1,…,n—V,使得
V二V1二:
:
:
1,…,n_r,V:
:
!
厂,n」。
令WK1,…,n」•,结论成立。
7.(北京师范大学2007;北京邮电大学2004)设v是数域F上的一个n维向量空间证明:
(1)V的任意一个真子空间都是V的若干个n-1维子空间的交。
(2)存在V的n-1维子空间V1,V2,V3使得
(V1V2)V3=(V1V3)(V2V3).
证明
(1)设W是V的任意一个真子空间,若dimW=n—1,那么结论显然成立。
若dimV=k:
:
:
n—1,不妨设W的一组基为:
-1/■k,那么有W-:
:
:
「,…「k•。
将〉1,…,7扩充为V的一组基,设为:
sm1「宀。
分别记
V1之>1,…,〉k,〉k.2,…Cn•,V2d:
〉1,…,〉k,〉k1,〉k・3「Cn•,…,V2=:
〉1,…,〉k,〉k・1,…,〉n_1-,
显然V1,V2,…,Vn上都是V的n一1维子空间,且
w=yv2Vz。
(2)任取V的n-1个线性无关的向量>1,…,〉n/「nd,记V1八n”,n「,贝U
V1是V的一个n-1维子真空间。
任取n.V,V1,则S—1不能由「厂」亠
线性表出,且〉1「・「nd线性无关,从而〉1「,〉n/「n4线性无关,记
V2之5…,:
—,",则V2是V的一个n-1维子真空间。
再任取—V,nJ*,njV,贝Un-1不能由〉1,n/线性表出,从而♦厂「n亠nX线性无关,记V3xa…,仁,n」,则V3也是V的一个n-1维子真空间。
以下验证这样构造的V1,V2,V3符合题目要求。
而ViV3-:
:
:
r,…
,:
n三,V?
V3=:
:
:
1,
所以
(ViV3)(V2V3)…1,…,:
n—是n-2维的,而V3是n-1维的,因此
(ViV?
)V3=(yV3)(V?
V3)成立。
8.设V-V2是数域F上线性空间v的两个非平凡子空间。
证明:
在V中存在向量,使得:
V1^■V2同时成立。
(书上习题)
一般情形:
(I)(北京大学2002)设V1,V2,…,Vs是数域F上n维线性空间v的s个非平凡子空间。
证明:
(1)V中至少存在一个向量:
不属于V1,V2,…,Vs中的任何一个。
(2)存在V中的一组基;2,…,;n,使得{;1,;2厂,;n}(V1V2Vs)-:
」。
证明
(1)对s做数学归纳法。
若s=1,结论显然成立。
设在s-1时结论成立,那么在s个真子空间的情形,由Vs是真子空间,那么
-Vs。
若「V1V2…vsJ,那么结论成立。
以下考虑一V1V2…vsJ的情形由归纳假设■V1V2…Vs」,若Vs,那么结论也成立。
因此只需考虑情形:
Y更